 |
Образцы задач к полной программе
|
|
|
|
ПРОГРАММА ЭКЗАМЕНА по математическому анализу
Для студентов групп ИДБ-15-10, ИДБ-15-11, ИДБ-15-17
(осенний семестр 2015/2016 учебного года)
Экзамен по ПРОГРАММЕ-МИНИМУМ проводится для всех студентов В экзаменационном билете 7 вопросов, в том числе несколько простых (типовых) задач. При ответе на теоретический вопрос доказательство не приводится. Для положительной оценки нужно правильно ответить на 5 (25 баллов), 6 (30 баллов) или все 7 (до 36 баллов) вопросов. Ответ на каждый вопрос должен быть изложен письменно на экзаменационном листе. Время на подготовку – 45 минут.
Студент, правильно ответивший на 6 или 7 вопросов, по желанию допускается к сдаче экзамена по ПОЛНОЙ ПРОГРАММЕ с оценкой до 54 баллов. В билет по этой программе входит теоретический вопрос и задача. При ответе на теоретический вопрос необходимо привести полное доказательство; возможны также дополнительные вопросы (в рамках программы). Общая оценка – не меньше той, которую студент получил при сдаче программы-минимум.
ПРОГРАММА-МИНИМУМ
В результате изучения дисциплины студент должен:
а) знать определения и обозначения следующих математических понятий, уметь приводить примеры, их иллюстрирующие –
числовая функция, основные элементарные функции, комплексное число, его действительная и мнимая части, модуль и аргумент, многочлен от одной переменой, последовательность, монотонная последовательность, ограниченная последовательность, число e, функция, ограниченная на данном множестве, бесконечно малая (б. м.) функция при 
(¥), эквивалентные б. м., б. м. высшего порядка по сравнению с данной и символ «o», приращение функции, непрерывность функции в точке, производная, дифференцируемость функции в точке, дифференциал, точка максимума (минимума, экстремума) функции.
|
|
|
б) знать следующие математические факты, формулы, формулировки теорем и утверждений –
геометрическое изображение комплексного числа и все формы его представления, формула Эйлера, основная теорема алгебры, теорема Вейерштрасса (достаточное условие сходимости последовательности), теорема о пределе суммы, произведения и частного двух функций, необходимое и достаточное условие непрерывности функции в точке, механический и геометрический смысл производной, таблица производных основных элементарных функций, необходимое и достаточное условие дифференцируемости функции, формула для вычисления дифференциала, достаточные условия возрастания и убывания функции на интервале, необходимое условие экстремума.
в) уметь –
строить простые графики на базе графиков основных элементарных функций, производить операции над комплексными числами, вычислять простейшие пределы (в частности, типа 
и 
, с применением теоремы о замене б. м. эквивалентными), использовать правила дифференцирования для вычисления производных явно и параметрически заданных функций, решать задачи на механический смысл производной, находить уравнения касательной и нормали к графику функции, применять дифференциал для приближенного вычисления приращения функции, использовать производные для исследования функций и строить простые графики, находить наименьшее и наибольшее значения функции на отрезке.
Образец экзаменационного билета по программе-минимум
1. 
? (Ответ: 
)
2. Достаточное условие сходимости последовательности (теорема Вейерштрасса).
3. Найти 
. (Ответ: 5/3)
4. Вычислить производную функции 
. (Ответ: 
)
5. Достаточное условие убывания функции 
на интервале.
6. Найти точки экстремума функции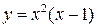 
. (Ответ: 
)
7. Построить график функции 
.
|
|
|
ПОЛНАЯ ПРОГРАММА
1. Формула Муавра. Корень n -й степени из комплексного числа.
2. Теорема Безу и её следствие. Разложение многочлена с действительными коэффициентами на линейные и квадратичные множители.
3. Предел последовательности. Число e, второй замечательный предел(формулировки).
4. Предел функции. Первый замечательный предел.
5. Теоремы о сумме бесконечно малых (б. м.) функций и о произведении б. м. функции на ограниченную. Связь между функцией, её пределом и б. м. функцией. Теорема о пределе произведения.
6. Теорема об ограниченности функции, имеющей предел. Теоремы о переходе к пределу в неравенстве.
7. Связь между бесконечно большими и бесконечно малыми функциями. Сравнение б. м. функций. Теорема о замене б. м. эквивалентными.
8. Необходимое и достаточное условие непрерывности функции в точке. Непрерывность суммы, произведения и частного непрерывных функций, сложной функции. Классификация точек разрыва. Непрерывность на отрезке. Теоремы Вейерштрасса(формулировки), Больцано-Коши(формулировки).
9. Необходимое и достаточное условие дифференцируемости функции. Непрерывность функции, имеющей производную. Правила нахождения дифференциала. Инвариантность формы дифференциала
10. Геометрический смысл производной. Бесконечная производная.
11. Правила дифференцирования произведения, сложной функции, обратной функции.
12. Производные функций sin x, ln x, log ax, cos x, tg x, ax, x a, arcsin x.
13. Теоремы Ферма и Ролля.
14. Теорема Лагранжа. Необходимое и достаточное условие постоянства функции на интервале. Достаточное условие возрастания (убывания) функции на интервале.
15. Теорема Коши. Правило Лопиталя для неопределенности типа 
при 
.
16. Необходимое и достаточное условие постоянства функции на интервале (отрезке).
17.Первое и второе достаточные условия экстремума функции одной переменной.
18. Необходимое и достаточное условие выпуклости вверх (вниз) графика функции на интервале(формулировка).
19.Достаточное условие выпуклости вверх (вниз) графика функции на интервале.
20.Точка перегиба. Необходимое условие точки перегиба. Достаточное условие точки перегиба.
21.Правило нахождения наклонных асимптот графика функции.
|
|
|
Образцы задач к полной программе
1. 
=? (Ответ: 
)
2. Под каким углом пересекаются линии 
? (Ответ: 
)
3. 
Существует ли 
? (Ответ: нет)
4. С помощью дифференциала найти приближенно 
.(Ответ: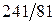 
).
5. Построить график функции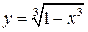 
.
6. 
? (Ответ: 
)
|
|
|
