|
Принцип суперпозиции. Связь между напряженностью и потенциалом. 24. Проводники в электрическом поле. Электростатическая защита. Электроемкость проводников. Конденсаторы
|
|
|
|
Принцип суперпозиции
 ,
, 
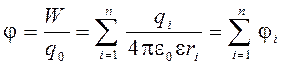 ,
,
т. е. потенциал поля, создаваемого системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности.
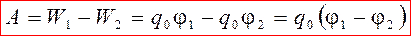 , (4)
, (4)
т. е. работа, совершаемая электрическими силами при перемещении заряда между двумя точками поля, равна произведению этого заряда на разность потенциалов в начальной и конечной точках пути.
Следствия:
1. работа перемещения заряда по замкнутому контуру равна нулю 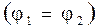 ;
;
2. работа положительна, если заряд q0 перемещается в направлении убывания потенциала 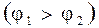 .
.
Графическое изображение электрических полей.
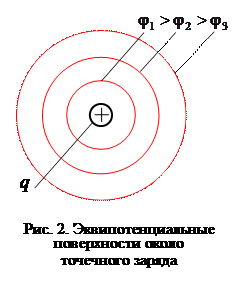
Эквипотенциальные поверхности
|
Эквипотенциальной поверхностью называется геометрическое место точек с одинаковым потенциалом (j=const).
Свойства эквипотенциальных поверхностей
· работа, совершаемая по перемещению заряда вдоль этой поверхности, равна нулю;
· кулоновская сила направлена перпендикулярно этой поверхности;
· эквипотенциальные поверхности не пересекаются;
· густота линий равного потенциала (число линий, проходящих через единицу площади) пропорциональна градиенту напряженности электрического поля;
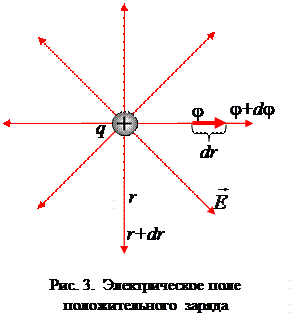
Связь между напряженностью и потенциалом
|
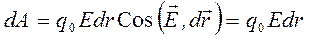 (5)
(5)
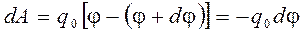 . (6)
. (6)
Приравнивая правые части уравнений (10, 11), получаем
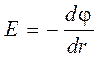 , (7)
, (7)
|
 , (8)
, (8)
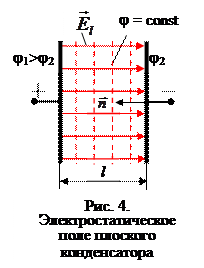
Пример. Для однородного поля плоского конденсатора (Е = const)
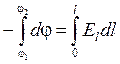 ,
, 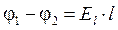 ,
, 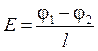 .
.
Единицы измерения
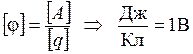 (Вольт);
(Вольт);

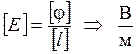 ;
;
Итак, электрическое поле, являясь полем потенциальным, имеет две характеристики – векторную или силовую 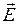 , и скалярную или энергетическую
, и скалярную или энергетическую 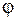 .
.
|
|
|
24. Проводники в электрическом поле. Электростатическая защита. Электроемкость проводников. Конденсаторы
Основной задачей электростатики является задача о нахождении напряженности  и потенциала j электрического поля в каждой точке пространства.
и потенциала j электрического поля в каждой точке пространства.
Теорема Гаусса
|
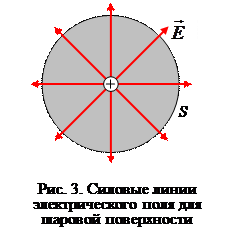
Потоком (ФЕ) вектора 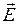 электрического поля через плоскую поверхность площади
электрического поля через плоскую поверхность площади 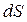 называется скалярная физическая величина, характеризующая интенсивность поля в данном месте пространства и численно равная количеству силовых линий, пронизывающих данную площадку в направлении нормали к ней.
называется скалярная физическая величина, характеризующая интенсивность поля в данном месте пространства и численно равная количеству силовых линий, пронизывающих данную площадку в направлении нормали к ней.

 , (1)
, (1)
Поток ФЕ, создаваемый единичным положительным зарядом
|
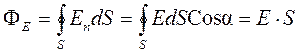 , (2)
, (2)
площадь шара 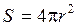 , напряженность поля точечного заряда
, напряженность поля точечного заряда 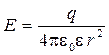 ,
,
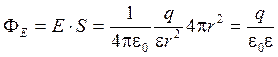 .
.
В общем случае: 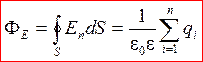 . (3)
. (3)
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ee0.
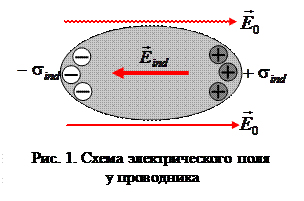
Проводником называется среда, в которой имеется достаточное число свободных электрических зарядов. Например, в металлах в 1 см3 содержится около 1023 свободных электронов.
Совокупность свободных электронов в металле называют электронным газом. Если проводник поместить в электрическое поле, то свободные электроны перемещаются внутри него под действием поля против силовых линий, в результате под действием внешнего электрического поля на поверхности пластины появятся индуцированные заряды с поверхностными плотностями 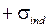 и
и  . Электрическое поле индуцированных зарядов компенсирует внешнее электрическое поле, т. е.
. Электрическое поле индуцированных зарядов компенсирует внешнее электрическое поле, т. е.
|
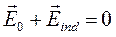 , т. к.
, т. к. 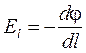 , то
, то
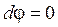 Þ
Þ 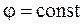 , (4)
, (4)
|
|
|
т. е. электростатическое поле внутри проводника отсутствует, а потенциал проводника является постоянным (проводник эквипотенциален).
|
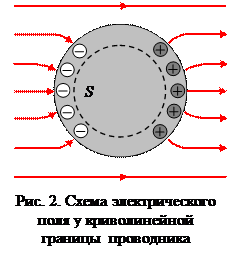
У криволинейной поверхности проводника силовая линия напряженности электростатического поля должна быть направлена по нормали к этой поверхности, иначе под действием тангенциальной составляющей поля 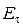 заряды перемещались бы по проводнику, что противоречит условию (4).
заряды перемещались бы по проводнику, что противоречит условию (4).
В заряженном проводнике избыточный заряд располагается только на поверхности, т. к. согласно теореме Гаусса для замкнутой области S внутри проводника заряд отсутствует.

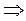
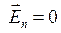
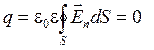 . (5)
. (5)
|
|
|