 |
Показатели ремонтопригодности
|
|
|
|
Модели надёжности программных систем.
Классификация моделей надежности программных средств
Свойство надежности является важным для многих искусственно созданных объектов. В Википедии оно определяется так: «Надёжность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования». Как правило, с надежностью связывают его эксплуатационные свойства, и прежде всего такие:
· безотказности,
· долговечности,
· ремонтопригодности
· сохраняемости,
а также их комбинацией.
В соответствии с ГОСТ 27.002-80 эти свойства уточняются следующим образом.
Показатели безотказности
1. Вероятность безотказной работы — вероятность того, что в пределах заданной наработки отказ системы не возникнет.
2. Вероятность отказа — обратная величина, вероятность того, что в пределах заданной наработки отказ системы возникнет.
3. Средняя наработка до отказа — математическое ожидание наработки системы до первого отказа (существенно для невосстанавливаемых систем).
4. Средняя наработка на отказ (То, MTBF — Main Time Between Failures) — отношение наработки восстанавливаемой системы к математическому ожиданию числа ее отказов в пределах этой наработки (имеет смысл только для восстанавливаемых систем).
5. Интенсивность отказов - условная плотность вероятности возникновения отказа невосстанавливаемой системы, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник.
6. Параметр потока отказов (X(t)) - отношение среднего числа отказов для восстанавливаемой системы за произвольно малую ее наработку к значению этой наработки.
|
|
|
Показатели долговечности
- Средний ресурс - математическое ожидание наработки системы от начала ее эксплуатации или ее возобновления после ремонта до перехода в предельное состояние.
- Срок службы (Tcc) - календарная продолжительность от начала эксплуатации системы или ее возобновления после ремонта до перехода в предельное состояние.
- Комплексные показатели надежности.
Показатели ремонтопригодности
- Вероятность восстановления работоспособного состояния - вероятность того, что время восстановления работоспособного состояния не превысит заданного.
- Среднее время восстановления работоспособного состояния (Tв) - математическое ожидание времени восстановления работоспособного состояния системы.
Надежность программного обеспечения одной из составляющих его качества, имеет важное значение и определяется как «... способность системы или компонента выполнять требуемые функции в заданных условиях на протяжении указанного периода времени».
В стандарте ISO 9126 надежность определяется как, способность программного обеспечения выполнять свои функции в заданных условиях. При этом это свойство составляется такими элементами:
- Зрелость (величина, обратная частоте критических отказов, вызванных ошибками в ПО).
- Устойчивость к отказам (способность поддерживать заданный уровень работоспособности при внутренних и внешних отказах).
- Способность к восстановлению (способность восстанавливать определенный уровень работоспособности и целостность данных после отказа).
· Соответствие стандартам надежности.
Проблема надежности имеет две стороны: оценка и обеспечение. Рассмотрим первую. Она решается применением моделей. Их можно классифицировать, прежде всего, на две группы: аналитические и эмпирические. Первые в свою очередь делятся на две группы: статические и динамические. Первые из них (статические) рассчитывая соответствующие метрики непосредственно, а вот вторые (динамические) - используют прогнозные модели. И первой, и во второй группе можно привести 6 конкретных моделей.
|
|
|
 |
Рис.5.19. Классификация моделей надежности.
Проблема оценки качества программного обеспечения ставит много задач, что приводит к множеству подходов, методов и средств. Еще одна классификация моделей надежности программных средств представлена на рисунке.
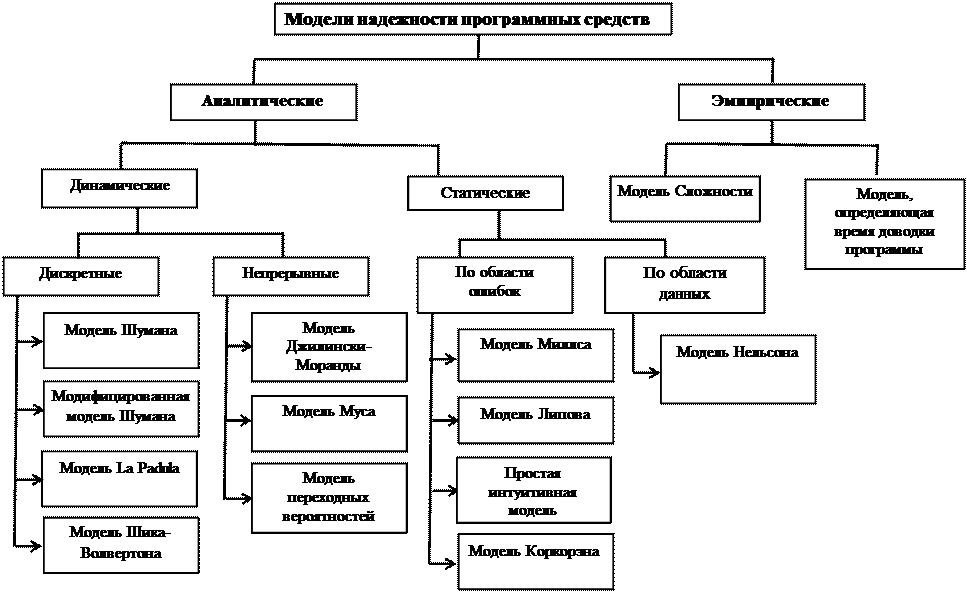
Рис.5.20. Другая классификация моделей надежности программного обеспечения
Приведем классификацию моделей надежности программного обеспечения, выделяющую три класса. Она основана на назначении моделей и предлагает их разделение на следующие три группы.
1. Прогнозные. Этот класс моделей формируется на этапе проектирования, и они позволяют рассчитать характеристики надежности программного средства до начала его отладки. Одна из метрик Холстеда (уравнение числа ошибок) принадлежит к этой группе. Она не рассматривается здесь, а приведена в разделе метрик, формируемых на основе лексического анализа программ. Модель Холстеда дает прогнозирование количества ошибок в программе в зависимости от ее объема и таких данных, как число операций (n1) и операндов (n2), а также их общее число (N1, N2).
2. Оценочные. Такие модели строятся на основе анализа результатов тестирования программ. Они позволяют на основе полученных значений характеристик надежности принимать решение о необходимости продолжать процедуру тестирования программного средства. К этой группе относятся такие модели: Джелинского—Моранды, Миллса и Простая Интуитивная или Эвристическая модель двух независимых групп тестирования Руднера.
3. Измерительные. На этапе испытания программного обеспечения, его сопровождения и эксплуатации (если это предусмотрено соответствующей документаций) строятся измерительные модели надежности программных средств. Модели Нельсона и Муса являются членам этой группы моделей.
Теперь перейдем к рассмотрению конкретных моделей.
Статические модели.
Модели, называемые статические не используют такого параметра как время, а связывают количества ошибок с числом тестовых прогонов или используют зависимость количества ошибок от характеристики входных данных. Первый тип моделей объединяют в группу с названием по области ошибок», а вторую - «по области данных».
|
|
|
Модель Миллса
Как и модель Джелински-Моранды (рассмотренная далее), модель надёжности Миллса относится к классу оценочных. По другой классификации эта модель относится к классу аналитических статических моделей, и ее применение предполагает внесение искусственных ошибок перед началом тестирования. Он фиксируются в специальном протоколе искусственных ошибок. При проведении тестирования могут быть найдены как искусственные, так и естественные ошибки, которые и должны быть выявлены в результате этой процедуры. Логичным предположением применения модели Миллса является тот факт, что как естественные, так и искусственные имеют равную вероятность быть обнаруженными в процессе тестирования. По этой методике, тестируя программу в течение некоторого времени, собирают данные об экспериментах. Предполагая равновероятное нахождение как внесенных в программу ошибок, так и имеющихся в ней ранее можно получить полезное соотношение
N = (S´n)/V.
Где N — первоначальное число ошибок в программе, S — количество искусственно внесенных ошибок, n — число найденных собственных ошибок, V — число обнаруженных к моменту оценки искусственных ошибок.
Однако методика Милса предполагает вычисление и еще одной полезной величины - мерой доверия к модели. Она рассчитывается по такой формуле
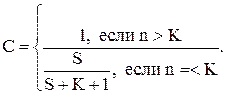
Здесь К – величина предполагаемого количества ошибок в программе.
Величина С оценивает вероятность правильного значения N. Можно сказать, что вторая формула оценивает качество значения полученного из первой формулы.
Другой случай представленный таким соотношением (вторая формула Миллс)
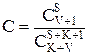
соответствует ситуации, когда были найдены не все внесенные ошибки. Она применяется в случае, когда V<S.
Рассмотрим конкретный пример на использование этой модели. Пусть в программу были преднамеренно внесены 10 ошибок. В результате тестирования обнаружено 12 ошибок, из которых 10 ошибок были внесены преднамеренно. Все обнаруженные ошибки были исправлены. Требуется определить количество ошибок до начала тестирования и степень отлаженности программы в предположении, что все преднамеренно внесенные ошибки будут обнаружены, а количество обнаруженных «собственных» ошибок программы не увеличится. Считается, что до тестирования максимальное количество предполагаемых ошибок равно двум.
|
|
|
Таким образом, нам дано:
· количество внесенных в программу ошибок S=10;
· количество обнаруженных ошибок, из внесенных в программу V=10;
· количество собственных ошибок в программе (обнаруженных при тестировании) n =12-10=2;
· верхний предел «собственных» ошибок в программе до начала тестирования K=2.
Используя первую формулу Миллса
 ,
,
Получим

Отсюда следует, что до тестирования в программе было 2 ошибки, которые были выявлены. Степень отлаженности для такой программы будет вычислена в соответствии с формулой

Для случая n=K она приведет к такому результату: С=10/(10+2+1)=10/13»0,76.
Теперь приведем еще один пример расчета с применением модели Миллса. Пусть в программу были преднамеренно внесены 10 ошибок. В результате тестирования обнаружено 15 ошибок, из которых 10 ошибок были внесены преднамеренно. Все обнаруженные ошибки были исправлены. Требуется определить количество ошибок до начала тестирования и степень отлаженности программы в предположении, что все преднамеренно внесенные ошибки будут обнаружены, а количество обнаруженных «собственных» ошибок программы не увеличится. Считается, что до тестирования максимальное количество предполагаемых ошибок равно четырем.
Таким образом, нам дано:
· количество внесенных в программу ошибок S=10;
· количество обнаруженных ошибок, из внесенных в программу V=10;
· количество собственных ошибок в программе (обнаруженных при тестировании) n =15-10=5;
· верхний предел «собственных» ошибок в программе до начала тестирования K=4.
Используя первую формулу Миллса
 ,
,
получим

Отсюда следует, что до тестирования в программе было 5 ошибок, которые были выявлены. Степень отлаженности для такой программы в соответствии с формулой для случая n>K

даст С=1.
Модель Липова.
Модифицированную модель Миллса предложил Липов [65]. В ней включив в нее вероятность обнаружения ошибки при использовании различного числа тестов. В ней, как и в модели Миллса считается, что собственные и искусственные ошибки имеют равную вероятность быть найденными. В методике Липова предложена такая формула
|
|
|
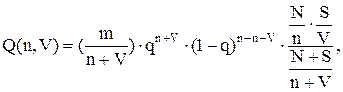
где N — первоначальное число ошибок в программе,
m - количество тестов,
S — количество искусственно внесенных ошибок,
n — число найденных собственных ошибок,
V — число обнаруженных к моменту оценки искусственных ошибок.
Применение рассматриваемой модели Липова требует выполнения следующие условия:
N>n>0; S>V>0; m>n+ V>0.
Достоинством модель Липова является то, что она позволяет оценить вероятность обнаружения некоторого количества ошибок к моменту оценки.
|
|
|


