 |
и отсюда мгновенное изменение относительной величины
|
|
|
|
Дифференциальное исчисление функции одной переменной
0. Введение.
1. Понятие производной функции.
2. Дифференцируемость функции в точке.
3. Непрерывность дифференцируемых функций.
4. Дифференцирование функций.
4.1. Правила дифференцирования функций.
4.2. Дифференцирование элементарных функций.
4.3. Логарифмическое дифференцирование.
5. Производная и дифференциал высших порядков.
6. Приложение дифференциального исчисления.
6.1. Вычисление пределов.
6.2. Геометрические приложения производной и дифференциала.
6.3. Исследование и построение графика функции.
6.4. Наибольшее и наименьшее значение функции на отрезке.
7. Приложение производной в экономике.
7.1. Эластичность функции.
7.2. Предельный анализ.
0.
1.
Важной характеристикой движения материальной точки является ее мгновенная скорость. Фиксируя произвольный момент времени 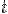 и какое угодно его приращение
и какое угодно его приращение 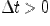 , получим среднюю скорость на отрезке времени
, получим среднюю скорость на отрезке времени 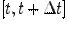

Находя средние скорости изменения различных функций, можно прийти к выводу: у одной и той же функции на различных отрезках средние скорости изменения различны; имеются функции, у которых средние скорости одинаковы на любом интервале. Таким образом, средняя скорость непостоянна, она зависит от момента времени 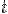 и от приращения времени
и от приращения времени 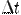 .
.
Исходя из этого, средняя скорость недостаточна для количественной оценки процесса изменения функции.
Теперь задача заключается в том, чтобы найти способ количественной оценки скорости изменении функции в каждой точке. Каждый раз, находя отношение ∆y/∆x, будем получать средние скорости изменения функции на все меньших интервалах изменения аргумента, т.е. в пределе при ∆x → 0 получим значение мгновенной скорости изменения функции в точке х.
|
|
|
Таким образом, количественная характеристика скорости изменения функции в точке равна lim ∆y/∆x
∆x → 0
Мгновенной скоростью (или просто скоростью) движущейся точки называется предел, к которому стремится средняя скорость 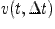 при стремлении к нулю приращения времени, т. е.
при стремлении к нулю приращения времени, т. е.
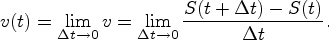
Этот предел будет иметь конечное значение, если только и числитель стремиться к нулю (приращение функции Δх→0).
На основании рассмотрения задач появляется новая математическая модель. Поэтому, чтобы изучить новую модель нужно:
1) присвоить ей специальный термин, придумать для нее специальное обозначение;
2) изучить правила оперирования с новой моделью;
3) изучить сферу приложения.
Итак, при нахождении скорости изменения какой-то переменной величины  в точке
в точке  нам нужно совершить предельный переход
нам нужно совершить предельный переход
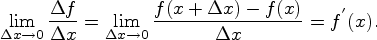 Данное символическое обозначение производной введено И. Ньютоном.
Данное символическое обозначение производной введено И. Ньютоном.
Число  , если такой предел существует, называется производной функции
, если такой предел существует, называется производной функции  в точке
в точке 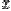 .
.
Пример 1. Найти производную функции f(x) = x2, в произвольной точке х по определению производной.
|
Из первого примера ∆f = 2x*∆x+∆x2, подставим, получим
|
|
|
2.
Рассмотрим приращение функции  в точке
в точке 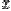
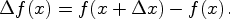
Поведение этого приращения, как функции приращения аргумента 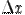 при фиксированном
при фиксированном 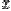 , показывает, существует ли производная в этой точке у функции
, показывает, существует ли производная в этой точке у функции  .
.
Если же приращение функции  в точке
в точке  может быть записано в виде
может быть записано в виде

то функция  называется дифференцируемой в точке
называется дифференцируемой в точке 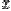 ., т.е. приращение функции в точке может быть представлено как сумма двух бесконечно малых величин с разным порядком малости. Первое слагаемое имеет первый порядок малости по отношению к ∆x, а второе – более высокий порядок, чем первый.
., т.е. приращение функции в точке может быть представлено как сумма двух бесконечно малых величин с разным порядком малости. Первое слагаемое имеет первый порядок малости по отношению к ∆x, а второе – более высокий порядок, чем первый.
|
|
|
Тем самым следует теорема 1: для того чтобы функция y = f(x), x є D, была дифференцируема в точке х0 є D, необходимо и достаточно, чтобы в этой точке существовал предел lim ∆y/∆x.
∆x → 0
Другими словами, для того чтобы y=f(x) была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке 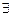 производная.
производная.
Доказательство:
необходимость: пусть f(x) дифференцируема в точке х, тогда по определению это значит ∆y=А∆х+α(∆х)∆х, А не зависит от ∆х, а α(∆х)→0 при ∆х→0.
 А=const, α-б/м, ∆х→0. По признаку предела
А=const, α-б/м, ∆х→0. По признаку предела 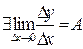 , следовательно функция имеет производную
, следовательно функция имеет производную 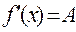
достаточность: пусть функция имеет производную в точке х, т.е. 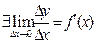 тогда по признаку
тогда по признаку
предела 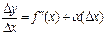 . Тогда при ∆х≠0 ∆y=
. Тогда при ∆х≠0 ∆y= 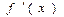 ∆х+α(∆х)∆х. Это означает, что f(x) дифференцируема А=
∆х+α(∆х)∆х. Это означает, что f(x) дифференцируема А= 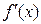 .
.
Замечание 1. Как видно из теоремы, необходимым условием дифференцируемости является существование производной. Для функции одной переменной дифференцируемость и существование производной — понятия равносильные.
Следствие 1. Отсюда следует, что при наличии дифференцируемости функции 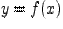 в точке
в точке 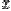 главную роль в приращении
главную роль в приращении  играет линейная часть
играет линейная часть 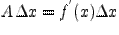 . Она называется дифференциалом функции
. Она называется дифференциалом функции  в точке
в точке 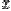 и обозначается
и обозначается

На примере линейной функции показывается, что дифференциал независимой переменной равен ее приращению dх = ∆x. Здесь 
Поэтому для любой дифференцируемой функции
dy = y´dx
y´ = dy/dх
Запись dy/dх часто используется для обозначения производной функции у по независимой переменной х. Данное обозначение производной широко используется в математике и было предложено Г. Лейбницем.
Необходимо показать, что ∆y есть бесконечно малая более высокого порядка, чем ∆x. Также dy и ∆y являются эквивалентными бесконечно малыми, т.е. ∆у ~ dy. Поэтому говорят, что дифференциал функции – главная линейная часть ее приращения.
3.
Также необходимо отметить связь между непрерывностью и дифференцируемостью функции в точке.
Теорема 2. если функция y = f(x), x є D, дифференцируема в точке х0 є D, то она непрерывна в этой точке.
Доказательство. Из существования  следует, что разность
следует, что разность
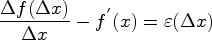 есть бесконечно малая функция при
есть бесконечно малая функция при 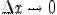 . Отсюда
. Отсюда
 и, следовательно, приращение функции
и, следовательно, приращение функции
|
|
|
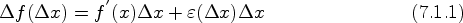
есть бесконечно малая функция при 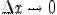 . Отсюда
. Отсюда  т.е.
т.е.  , что означает непрерывность функции
, что означает непрерывность функции 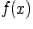 в точке
в точке 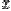 .
.
С другой стороны необходимо показать, что существуют функции, непрерывные, но не дифференцируемые, например, функции у=х и у=³√х не дифференцируемы в точке х = 0. Иными словами, множество дифференцируемых функций представляет собой подмножество множества непрерывных функций.
Пример 1. Функция  непрерывна в точке
непрерывна в точке  , но производная в точке
, но производная в точке  не существует, так как не существует предел
не существует, так как не существует предел 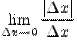 .
.
у=³√х
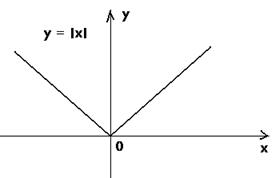 | 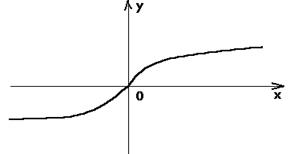 | ||
При геометрическом истолковании видно, в этой точке первая функция имеет излом, вторая – точку перегиба. Отсюда делается вывод: что если функция имеет точку излома и точку перегиба, то она в этой точке не дифференцируема.
4.
Для вычисления производной выведены правила нахождения производной и таблицы производных элементарных функций.
4.1.
Пусть функции  и
и 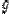 имеют производные в точке
имеют производные в точке 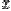 . Тогда существуют производные в левых частях следующих равенств и имеют место правила:
. Тогда существуют производные в левых частях следующих равенств и имеют место правила:
1) Производная суммы
 ;
;
2) Производная произведения
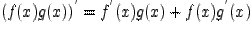
Доказательство.
 ;
;
3) Правило частного
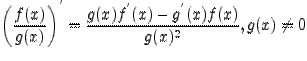
4) Правило производной сложной функции
Теорема 1. Пусть задана сложная функция 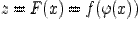 ;
;
функция 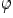 имеет производную в точке
имеет производную в точке  , а функция
, а функция  имеет производную в точке
имеет производную в точке  . Тогда функция
. Тогда функция 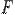 имеет производную в точке
имеет производную в точке  и
и 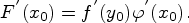
Доказательство. Так как функция 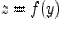 дифференцируема в точке
дифференцируема в точке  , то
, то
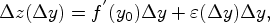 где
где 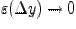 при
при 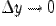 . Если положить
. Если положить 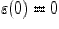 , то функция
, то функция  непрерывна в точке
непрерывна в точке 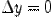 . Придадим переменной
. Придадим переменной 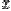 в точке
в точке  малое приращение
малое приращение 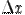 ; оно влечет приращение зависимой переменной
; оно влечет приращение зависимой переменной 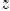 :
: 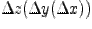 . Итак,
. Итак,
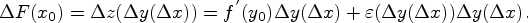 Разделив на
Разделив на  , получим
, получим

Так как существует 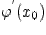 , то функция
, то функция  непрерывна в точке
непрерывна в точке  и, следовательно,
и, следовательно,  при
при 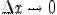 , и так как
, и так как 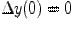 , то функция
, то функция  непрерывна в точке
непрерывна в точке 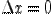 . Отсюда сложная функция, как суперпозиция непрерывных функций
. Отсюда сложная функция, как суперпозиция непрерывных функций 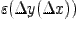 , непрерывна в точке
, непрерывна в точке 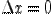 . Теперь, переходя к пределу в (7.3.1) при
. Теперь, переходя к пределу в (7.3.1) при 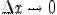 , получим
, получим 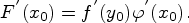
Замечание 1. Правило позволяет вычислить производную сложной функции, если известны производные составляющих ее функций.
Пример 1. 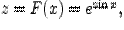

Тогда 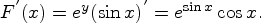
Следствие 1. Из теоремы следует инвариантность формы первого дифференциала. Если задана функция от функции 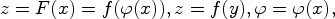 то дифференциал зависимой переменной
то дифференциал зависимой переменной 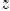 равен произведению производной от нее по одной из переменных
равен произведению производной от нее по одной из переменных 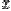 или
или 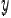 на дифференциал по этой переменной, причем неважно, зависимая эта переменная или нет. Действительно,
на дифференциал по этой переменной, причем неважно, зависимая эта переменная или нет. Действительно, 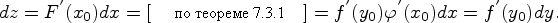
|
|
|
Пример 2. Найдем дифференциал функции 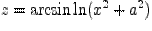 :
:
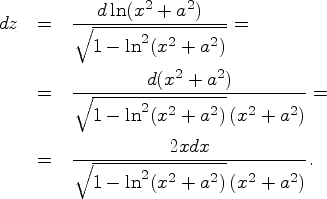
5) Правило производной обратной функции
Теорема 7.4.1. Пусть функция 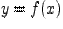 определена, непрерывна и строго монотонна в некоторой окрестности точки
определена, непрерывна и строго монотонна в некоторой окрестности точки  , и пусть в этой точке производная
, и пусть в этой точке производная  . Тогда и обратная функция
. Тогда и обратная функция  имеет производную в точке
имеет производную в точке 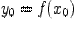 , причем
, причем

Доказательство. Зафиксируем некоторый отрезок с центром в точке 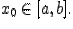 На отрезке
На отрезке  функция
функция  строго монотонна (пусть возрастающая), непрерывна. Тогда по существует обратная к ней функция
строго монотонна (пусть возрастающая), непрерывна. Тогда по существует обратная к ней функция  непрерывная и строго возрастающая на отрезке
непрерывная и строго возрастающая на отрезке  . Поскольку функции
. Поскольку функции  и
и  непрерывны в точках
непрерывны в точках  и
и 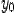 , то при
, то при 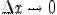 ,
, 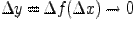 ; при
; при 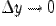 ,
, 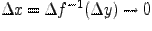 . Из строгой монотонности следует, что
. Из строгой монотонности следует, что 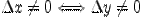 . Рассмотрим
. Рассмотрим
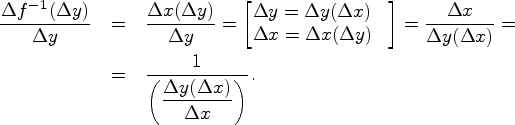
Итак, поскольку 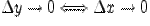 , имеем
, имеем

Пример 1. 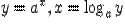 ,
, 
Пример 2. 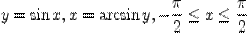 ,
,

Пример 3.  ,
,
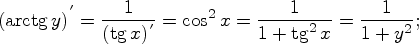
Пример 4.  .
.
Из теорем о производных суммы, произведения и частного можно получить аналогичные формулы для дифференциалов суммы, произведения и частного.
Пусть функции 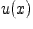 и
и 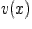 дифференцируемы в точке
дифференцируемы в точке 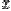 , тогда имеют место равенства:
, тогда имеют место равенства:
1) 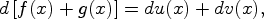
2) 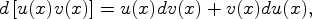
3) 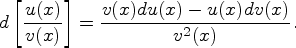
Замечание 1. На практике часто бывает выгоднее оперировать дифференциалами, а потом делением на дифференциал независимой переменной переходить к производной.
4.2.
Таблица производных элементарных функций
1) 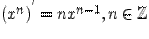 и n Є R; В частности C` = 0, C – const, x` = 1
и n Є R; В частности C` = 0, C – const, x` = 1
2)  ;
;
3)  ; где a>0, a≠1
; где a>0, a≠1
4)  .
.
Доказательство
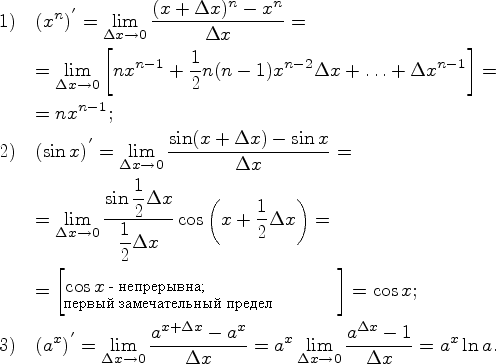
4) (ln x)` = 1/x
5) (ctg x)` = - 1/(sin x)2
6) (arcsin x)` = 1/ 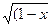 2)
2)
7) (arccos x)` = - 1/ 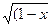 2)
2)
8) (arctg x)` = 1/(1 + x2)
9) (arcctg x)` = - [1/(1 + x2)]
Формулы нахождения дифференциала основных элементарных функций можно написать самим, умножив соответствующее правило взятия производной на dx.
Например, d sinx = (sinx)`dx = cosx dx.
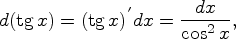
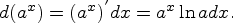
Пример 1. Найти производную от функции у=3х4 – 2х2 + 1.
Решение: у` = 3*4х3 – 2*2х + 0 = 12х3 – 4х.
Пример 2. Найти производную от функции у = x2 *℮х.
Решение: у` = (x2)` *℮х + x2 *(℮х)` = 2x ℮х + x2 *℮х ln℮, ln ℮ = log℮℮ = 1.
y` = 2x℮x + x2 * ℮x
Пример 3. Дана функция у = х/(х2+1). Найти у`.
Решение у` = [1*(х2+1) – х*2х] / (х2+1)2 = [х2+1 – 2х2] / (x2 +1)2 = (1-x2) / (x2+1)2
Пример 4. у = (1-х2)3; у`= 3(1 –х2)2 * (-2х)
Пример 5. у = sin2х; у` = 2sinx * cosx.
Пример 6. Найти dy, если у = sin 3х
Решение dy = у` * dx = (sin3x)` dx = (cos3x) * 3dx = 3 cos3x dx.
Пример 7. Найти dy, если у = 2х^2
Решение: dy = y` * dx = (2x^2)` * dx = 2x^2 ln2 * 2xdx
Пример 8.
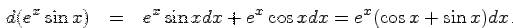
4.3.
Необходимо отметить, что во многих случаях при нахождении производных частного двух функций, произведения нескольких функций, показательно-степенных функций лучше пользоваться формулой логарифмического дифференцирования. Так как, пользуясь свойствами логарифма гораздо легче находить производные.
|
|
|
5.
Нетрудно заметить, что если функция, определенная в области определения, имеет производную во всех точках области определения, то эту производную можно принять за новую функцию. Тогда, к этой функции применимы все предельные законы, в том числе и вычисление производной, т.е. дифференцирование. Если полученная функция имеет конечную производную, то значение этой производной будет называться второй производной (производной второго порядка) для исходной функции. Эту процедуру вычисления производных высшего порядка можно распространить на третий, четвертый и т.д.
Пусть мы нашли от функции у = f(х) ее производную у` = f `(х). Производная от этой производной и называется производной второго порядка от функции f(х) и обозначается у`` или f `` (х) или (d2y) / (dx2). Аналогично определяются и обозначаются: производная третьего порядка у``` = f ```(x) = (d3y) / (dx3). Производная четвертого порядка у(4) = f (4)(x) = (d4y) / (dx4). Производная n-oго порядка у(n) = f (n)(x) = (d n y) / (dxn).
Пример 1.  ,...;
,...;
Пример 2. 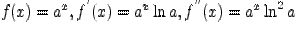 ,...;
,...;
Пример 3. 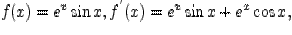
 .
.
Пример 4: у = 5х4 – 3х3 + 2х – 2. Найти у``.
Решение. Находим в начале первую производную: у` = 20х3 – 9х2 +2, потом вторую от первой производной: у`` = 60х2 – 18х.
Пример 5. y=хsinx. Найти у```.
Решение. y` = sinx + xcosx
y`` = cosx + cosx – x sinx = 2cosx – x sinx
y``` = -2sinx – sinx – x cosx = -3sinx – x cosx.
Пусть функция 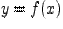 дифференцируема в некотором интервале
дифференцируема в некотором интервале 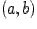 и
и 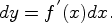 Здесь дифференциал
Здесь дифференциал 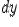 есть функция двух переменных --
есть функция двух переменных -- 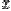 и
и  :
:
 Пусть производная
Пусть производная 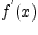 дифференцируема в точке
дифференцируема в точке  . Тогда дифференциал в этой точке функции
. Тогда дифференциал в этой точке функции 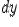 , если рассматривать его как функцию только от переменной
, если рассматривать его как функцию только от переменной 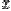 при фиксированной второй переменной
при фиксированной второй переменной  , имеет вид (обозначим его
, имеет вид (обозначим его 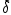 , в отличие от
, в отличие от 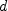 для первого дифференциала)
для первого дифференциала)
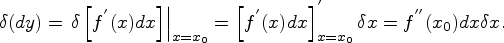
Вторым дифференциалом  функции
функции 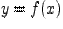 в точке
в точке  называется дифференциал от
называется дифференциал от 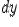 (т. е. дифференциал от первого дифференциала
(т. е. дифференциал от первого дифференциала 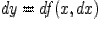 , как функции от переменной
, как функции от переменной 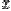 при фиксированной переменной
при фиксированной переменной  ):
):
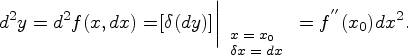
Аналогично определяются дифференциалы более высоких порядков:
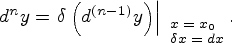
6.1.
Теорема (Правило Лопиталя). Пусть функции  и
и 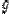
 дифференцируемы в выколотой окрестности
дифференцируемы в выколотой окрестности 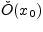 точки
точки 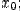
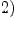
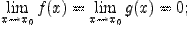
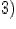
 для всех
для всех 
 существует предел, конечный или бесконечный,
существует предел, конечный или бесконечный,
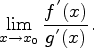
Тогда существует и предел
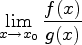 и имеет место равенство
и имеет место равенство 
Доказательство проведем для случая 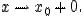 Функции
Функции  и
и 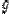 непрерывны на некотором интервале
непрерывны на некотором интервале 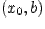 как дифференцируемые на нем функции. Доопределим функции
как дифференцируемые на нем функции. Доопределим функции  и
и 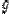 в точке
в точке  :
: 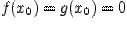 . Таким образом, они становятся непрерывными на отрезке
. Таким образом, они становятся непрерывными на отрезке  . Возьмем любое
. Возьмем любое  , тогда на отрезке
, тогда на отрезке 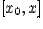 функции
функции  и
и 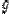 удовлетворяют условиям теоремы Коши о среднем значении, поэтому существует точка
удовлетворяют условиям теоремы Коши о среднем значении, поэтому существует точка 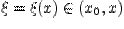 такая, что
такая, что 
Заметим, что 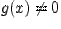 , иначе по теореме Ролля
, иначе по теореме Ролля 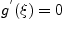 в некоторой точке
в некоторой точке 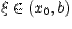 . Ясно, что и здесь
. Ясно, что и здесь  при
при  . Поэтому, по правилу вычисления предела сложной функции, имеем
. Поэтому, по правилу вычисления предела сложной функции, имеем
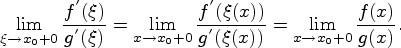
Пример 1.

Сформулируем еще одно правило.
Теорема (Правило Лопиталя). Пусть функции  и
и 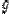
 дифференцируемы на интервале
дифференцируемы на интервале 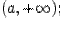
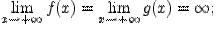
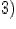
 на
на 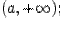
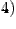 существует конечный или бесконечный
существует конечный или бесконечный 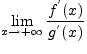 .
.
Тогда существует и предел 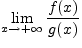 , и они равны.
, и они равны.
Пример 2. Пусть  .
.

6.2.
Мы предлагаем придерживаться следующей схемы:
1. Нахождение области определения функции.
2. Исследование функции на периодичность.
3. Исследование функции на четность.
4. Исследование функции на непрерывность, поведение функции на границах области определения (нахождение точек разрыва, установление характера разрыва, нахождение асимптот).
5. Нахождение точек пересечения графика с осями координат и определение интервалов знакопостоянства функции.
6. Исследование функции на монотонность, нахождение точек экстремума.
7. Исследование направления выпуклости графика функции, нахождение точек перегиба.
8. Составление таблицы значений функции для некоторых значений ее аргумента.
9. Используя все полученные результаты, построение графика функции.
Рассмотрим более подробно исследование функции y= f(x) по схеме.
1. Как найти область определения функции?
- Это те точки, в которых функция существует.
2. Как исследовать функцию на периодичность?
- Период имеют только тригонометрические и им обратные функции. Если функция периодична, то ее достаточно исследовать на этом периоде.
3. Как исследовать функцию на четность?
- Необходимо найти функцию от –х, тогда: если y(-x)= y(x), то функция четна; если же y(-x)=-y(x), то функция нечетна; в остальных случаях функция не является четной и нечетной. Следовательно, если функция четна, то ее достаточно исследовать, например, на промежутке х≥0, затем симметрично относительно оси ординат; если функция нечетна, то ее достаточно исследовать, например, на промежутке х>0, затем симметрично относительно начало координат; в остальных случаях функция исследуется на всей области определения.
4. Как исследовать функцию на непрерывность?
- Функция непрерывна на всей своей области определения. Необходимо только исследовать поведение функции на границах области определения, т.е. найти точки разрыва и установить характер разрыва (первого, второго рода). Исходя из этого, найти асимптоты: вертикальная х=а -точка разрыва второго рода; наклонная у=kx+b – согласно формулам (k=lim y/x при х→∞, b=lim(y-kx) при х→∞) и если k = 0, существует горизонтальная асимптота.
5. Как определить интервалы знакопостоянства функции? Как найти точки пересечения с осями?
- Интервалы знакопостоянства функции – интервалы, на которых функция сохраняет свой знак, т.е., найти интервалы, где функция положительна, где отрицательна. Чтобы найти точки пересечения с осью абсцисс, надо найти значение у, при которых х=0; а с осью ординат – значение х, при которых у=0.
6. Как исследовать функцию на монотонность и найти точки экстремума?
- Сначала необходимо рассмотреть геометрический смысл производной:

Производная f’(x) численно равна угловому коэффициенту касательной k, где k=tgα.
Отсюда, вытекает свойство о существовании касательной: Для того чтобы существовала невертикальная касательная к графику функции в любой точке графика, необходимо и достаточно, чтобы функция была дифференцируемой в данной точке.
При геометрическом истолковании видно,
 |  | ||
у=³√х
что в точке х=0 первая функция имеет излом, вторая – точку перегиба. В данной точке не существует касательной, тогда функция не дифференцируема в данной точке.
Таким образом, производная позволяет характеризовать поведение функции лишь вблизи от данной точки. Часто возникает необходимость делать выводы о поведении функции на всей области ее задания, что позволяют сделать теоремы об экстремуме, Ролля, Лагранжа.
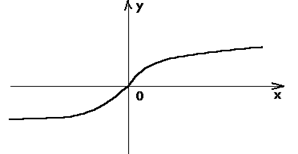
Сравнивая значения функции в точке х1 (х2) со значением функции в точках, «близких» к х1 (х2) делается вывод:
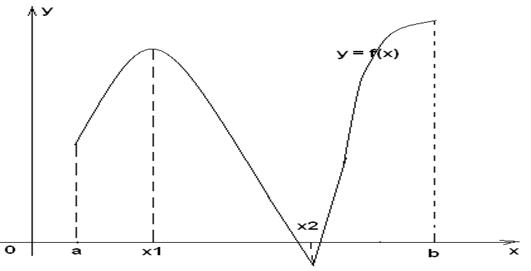
Существует такая окрестность точки х1 , что для любого х из этой окрестности выполняется неравенство f(x) ≤ f(x1). Функция y=f(x)в точке х1 имеет максимум.
Существует такая окрестность точки х2 , что для любого х из этой окрестности выполняется неравенство f(x) ≥ f(x2). Функция y=f(x)в точке х2 имеет минимум.
Необходимо отметить, что окрестность, о которой говорится в определении, не единственная; это можно показать на чертеже. Важно, что она в каждом из указанных случаев существует. Понятия максимума и минимума локальны.
Значения функции в точках максимума больше, чем значения функции в точках некоторой окрестности. Это не означает, что значения функции в точках максимума вообще больше всех значений функции. Более того, значения функции в некоторых точках максимума меньше, чем в некоторых точках минимума.
Если функция определена на отрезке, то концы отрезка не могут быть точками максимума и минимума, так как для этих точек нельзя подобрать содержащего их интервала, целиком входящего в область определения рассматриваемой функции.
Рассматривая график, очевидно, что в точке х1 к графику функции можно провести касательную, причем она параллельна оси Ох, значит в этой точке производная существует и равна нулю. А в точке х2 производная не существует. Это наблюдение позволяет сделать вывод, что если функция y = f(x), непрерывная в некоторой окрестности, имеет экстремум в точке х0, то в этой точке производная данной функции либо не существует, либо равна нулю (теорема).
Теорема Ролля. Пусть функция y=f(x) удовлетворяет следующим условиям: 1) непрерывна на отрезке [a;b]; 2) дифференцируема в интервале (a;b); 3) на концах отрезка[a;b] принимает равные значения: f(a)=f(b). Тогда в интервале (a;b) существует, по крайней мере, одна точка с, производная в которой равна нулю.
Доказательство.
Из условия непрерывности функции на отрезке следует, что функция на этом отрезке принимает свое наименьшее значение m и свое наибольшее значение M.
Возможны два случая: 1) значения m и М данная функция принимает на концах отрезка; 2) хотя бы одно из значений m и М данная функция принимает во внутренней точке отрезка.
Рассмотрим первый случай.
Из условия теоремы следует, что наименьшее значение функции на отрезке совпадет с ее наименьшим значением, и потому данная функция на этом отрезке постоянна. Следовательно, всюду на этом отрезке ее производная равна нулю, и в качестве точки с можно выбрать любую.
Рассмотрим второй случай.
Для определенности пусть f(c)=M, где с лежит внутри отрезка, т.е. точка с является точкой максимума. Согласно предыдущей теореме, следует f’(c)=0.
Рассмотрим общий случай, когда f(a)≠f(b). §
Геометрический смысл: на графике непрерывной дифференцируемой функции всегда отыщется точка А(x0,f(x0)), в которой касательная к графику функции параллельна оси Ох (такая точка м/б и не одна).
Теорема Лагранжа. Пусть функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема во всех внутренних точках отрезка. Тогда в интервале (a;b) найдется точка с (a<c<b), в которой выполняется равенство
f’(c)=(f(b)-f(a))/(b-a).
Доказательство.
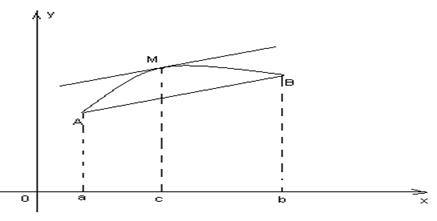
Сравнивая с теоремой Роля, видно, что в данной теореме не выполняется третье условие. Чтобы можно было применить теорему Ролля, необходимо составить такую функцию F(x), у которой F(a)=F(b). Рассмотрим F(x)=укривой-ухорды= f(x)-(kx+l).
Вспомогательная функция F(x) удовлетворяет всем условиям Теоремы Ролля.
Отсюда следует, что в интервале (а; b) найдется, по крайней мере, одна точка с, производная в которой будет равна нулю, т.е. F́(x) =f́ (x) – k. Существует с, что
f́ (с) – k = 0. Таким образом, k(хорды) = (f(a)-f(b))/(b-a).
f́ (с)= (f(a)-f(b))/(b-a). §
Геометрический смысл: на графике непрерывной дифференцируемой на отрезке [a,b] функции 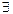 точка M(c,f(c)), в которой касательная к графику функции f(x) параллельна хорде, соединяющей точки A(a,f(a)) и B(b,f(b)). Такая точка может быть и не одна.
точка M(c,f(c)), в которой касательная к графику функции f(x) параллельна хорде, соединяющей точки A(a,f(a)) и B(b,f(b)). Такая точка может быть и не одна.
Теорема Коши: пусть 2 функции f(x) и g(x) удовлетворяют условиям: 1) f(x) и g(x) непрерывны на [a,b]; 2) f(x) и g(x) дифференцируемы в (a,b); 3) g'(x)≠0 в (a,b), тогда в (a,b) 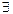 такая точка с, что имеет место формула Коши:
такая точка с, что имеет место формула Коши: 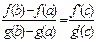
Данные теоремы часто называют теоремами о среднем в дифференциальном исчислении.
Теперь можно определить связь монотонности функции с производной. При геометрическом истолковании видно:
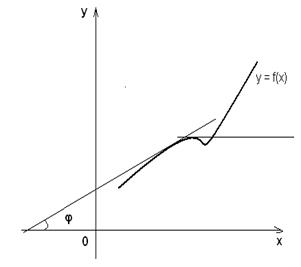
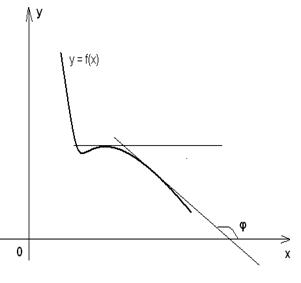
что, если дифференцируемая функция возрастает, то касательная к графику функции в любой точке либо составляет с положительным направлением оси абсцисс острый угол, либо параллельна оси абсцисс. Если же дифференцируемая функция убывает, то касательная к графику функции в любой точке либо составляет
|
|
|


