 |
Параметры свободных колебаний
|
|
|
|
Кафедра механики
РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ №1
|
По дисциплине:
 (наименование учебной дисциплины согласно учебному плану)
(наименование учебной дисциплины согласно учебному плану)

Вариант-3
Тема: Собственные колебания консервативной системы с одной степенью свободы вблизи положения равновесия.
Выполнил: студент гр. РТ-04 ____________ / Бойко Т.В. /
(подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: __________________
ПРОВЕРИЛ: профессор ____________ /Горшков Л. К./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
Задание:
Схема колебательной системы:

1 - груз массой m1;
2 - бицилиндр m2,  2, r2,R2;
2, r2,R2;
3 - балка m3.
Параметры системы
Таблица 1
| m1,кг | m2,кг | m3,кг | r2,cм | R2, cм | ρ, cм | C, Н/м | l, см | η0, см |  , см/с , см/с
| d =k/n |
| 0,24 | 1,6 |
Свободные колебания
Кинетическая энергия
Общая кинетическая энергия системы:

Кинетическая энергия возвратно- поступательного движения груза:

где  - обобщенная скорость, м/с.
- обобщенная скорость, м/с.
Кинетическая энергия вращающегося бицилиндра вокруг неподвижной оси:

где I2 – осевой момент инерции бицилиндра, кг∙м2;
ω2 –угловая скорость вращения бицилиндра.
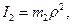
где ρ – радиус инерции бицилиндра, м.

Окончательный вид формулы нахождения кинетической энергии бицилиндра:

Кинетическая энергия стержня, вращающегося относительно оси, проходящей через точку О1:
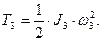
Момент инерции стержня:

Угловая скорость стержня:
Учитывая малость колебаний, будем считать скорости в точках В и С одинаковыми:

Окончательный вид формулы нахождения кинетической энергии стержня:
|
|
|
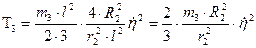
Общая кинетическая энергия системы:

где m – обобщенная масса системы.

 .
.
Потенциальная энергия
Потенциальная энергия системы определяется работой сил тяжести системы и силы упругости пружины на перемещении системы из отклоненного положения, когда груз имеет координату  , в положение статического равновесия. При таком отклонении вес блока (бицилиндр) работы не производит, поэтому потенциальная энергия системы равна:
, в положение статического равновесия. При таком отклонении вес блока (бицилиндр) работы не производит, поэтому потенциальная энергия системы равна:

Потенциальная энергия груза:

Минус ставится, так как груз из положения статического равновесия отклоняется вниз при положительном  .
.
Потенциальная энергия стержня:

 |

Исходя из малости колебаний, угол  очень мал, и можно заменить синус соответствующим углом.
очень мал, и можно заменить синус соответствующим углом.
 ,
, 
Смещение BB1 совпадает с перемещением точки, лежащей на поверхности блока, т.е.  тогда
тогда  ,
, 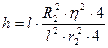

Потенциальная энергия пружины:
 ,
,
где С – жесткость пружины, Н/м,
λ – динамическая деформация, м,
λст – статическая деформация, м.


Полная потенциальная энергия системы:

 .
.
В положении, соответствующем  , система находится в равновесии. Поэтому должно выполняться условие:
, система находится в равновесии. Поэтому должно выполняться условие: 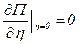 .
.

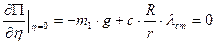
|


 ,
,
где μ – обобщенная жесткость системы, Н/м.
Подставим численные значения:

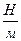

Уравнение Лагранжа

Найдем составляющие этого уравнения для нашей системы:
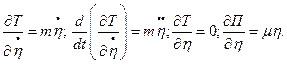
 (уравнение Лагранжа данной колебательной системы).
(уравнение Лагранжа данной колебательной системы).
Дифференциальное уравнение колебаний
Уравнение Лагранжа с численными коэффициентами:

Это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Закон колебаний
Для решения дифференциального уравнения колебаний, нахождения его интеграла, надо составить характеристическое уравнение:


Решение данного уравнения зависит от знака  . В данном случае
. В данном случае  ,
,
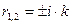 ,
,
где  - круговая частота колебаний, рад/с;
- круговая частота колебаний, рад/с;
|
|
|
 - мнимая единица.
- мнимая единица.




Для корней мнимых и сопряжённых, решение дифференциального уравнения колебаний:


 - постоянные интегрирования, определяемые из начальных условий.
- постоянные интегрирования, определяемые из начальных условий.
Из первого начального условия:
 -начальная координата.
-начальная координата.

Для использования второго начального условия  возьмём производную от
возьмём производную от  :
:

Из второго начального условия:

Таким образом, закон колебаний будет записан:
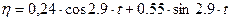 , см
, см
Представим закон колебаний в виде синусоиды:
 ,
,
где а – амплитуда колебаний 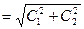 , м;
, м;
 - начальная фаза колебаний
- начальная фаза колебаний  , рад.
, рад.
Амплитуда колебаний:

Начальная фаза колебаний:
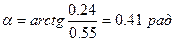 .
.
Окончательный вид закона колебаний:
 , см
, см
Параметры свободных колебаний
Параметрами свободных колебаний являются: период, частота, амплитуда, начальная фаза. Для амплитуды и начальной фазы значения были вычислены ( ,
,  ).
).
Период колебаний:

Частота колебаний:

График колебаний

Затухающие колебания
Коэффициент уменьшения частоты собственных колебаний  ;
;
удельный коэффициент демпфирования  ;
;
круговая частота затухающих колебаний
 ;
;
период затухающих колебаний  ;
;
абсолютная частота затухающих колебаний  .
.
Дифференциальное уравнение колебаний с учетом сопротивления:

1,46- удвоенное значение коэффициента демпфирования n.
Решением данного уравнения будет являться выражение:
 .
.
Определим постоянные интегрирования, используя начальные условия:




Представим закон колебаний в виде синусоиды:

Амплитуда колебаний:

Начальная фаза колебаний:
 .
.
Окончательный вид закона колебаний:
 , см
, см
|
|
|


