 |
Симметрия кристаллической структуры
|
|
|
|
По симметрии и числу единичных направлений кристаллы делятся на три категории: высшую, среднюю и низшую. Три категории в свою очередь делятся на 7 сингоний: триклинная, моноклинная, ромбическая, тригональная, гексагональная, тетрагональная и кубическая.
Nb, как и V имеет решетку ГЦК кубической сингонии, относящейся к высшей категории.
Кристаллы высшей категории не имеют единичных направлений. У них обязательно есть несколько осей порядка выше чем 2, в частности четыре оси 3, расположенные как пространственные диагонали куба. Любому направлению в кристалле высшей категории соответствуют симметрично эквивалентные направления. Многие физические свойства (электропроводность, теплопроводность) в этих кристаллах изотропны, как в аморфных веществах, а анизотропия других свойств (упругость, электрооптический эффект) гораздо слабее чем у кристаллов других категорий. Внешняя форма кристаллов как правило изометрична, т.е. развита примерно одинаково во всех направлениях, как куб, октаэдр, тетраэдр.
Для кубической сингонии характерно четыре оси и отсутствие единичных направлений.
Классом симметрии называют полную совокупность операций симметрии (возможных симметричных преобразований) этого объекта.
Nb и V, как и все металлы с кубической решеткой относятся к классу симметрии m3m (имеет 4 оси симметрии проходящие по биссектрисам координатных углов, ось 4-го порядка, центр симметрии, три координатные и шесть диагональных плоскостей симметрии)
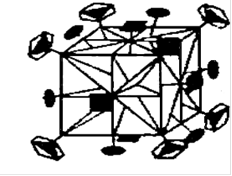
Рисунок 3- Комплекс элементов симметрии m3m.
Междоузлия кристаллической решетки
Междоузлие в идеальном кристалле - это свободное пространство между занятыми атомами узлами кристаллической решетки. Разделяют два вида междоузлий: октаэдрические (октапоры) и тераэдрические (тетрапоры) пустоты, в зависимости от формы. Междоузлия характеризуются размером, за который принимают радиус шарика, который вписывается в эту пору
|
|
|
В ГЦК решетке на ячейку приходится 4 октапоры (1 октапора на атом) с координатами:
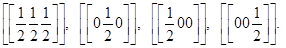
На Рисунке 4 крестиками обозначены центры октапор в ячейке решетки ГЦК
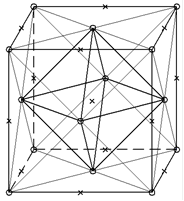
Рисунок 4 - Расположение октапор в ячейке ГЦК решетки.
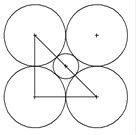
Рисунок 5 - Расположение атомов в плоскости (002).
Вычислим размер октапоры:
В ГЦК решетке соотношение между атомным радиусом и периодом решетки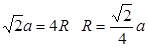 
, из рисунка 1.6 с применением теоремы Пифагора получаем:
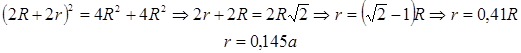
На ячейку решетки ГЦК приходится 8 тетрапор (по 2 тетрапоры на атом), с координатами
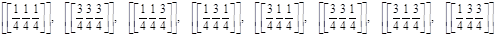
На рисунке 6 крестиками показаны центры тетрапор.
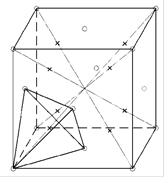
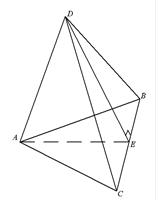
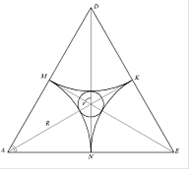
Рисунок 6 - Расположение Рисунок 7 - Тетрапора(а) и одна из тетрапор в ячейке ГЦК решетки плоскостей в ней(б)
Для вычисления размера тетрапоры вынесем тетрапору на отдельный рисунок (рисунок 1.8а) и выделим один из треугольников (рисунок 1.8б)
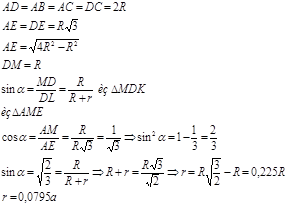
Фазовые равновесия
Кристаллическая структура. Кривая изменения параметра решетки в зависимости от состава сплавов показывает небольшое положительное отклонение от правила Вегарда, параметр решетки измерялся с точностью ±0,005 нм.
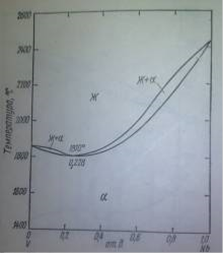
Рисунок 8 - Диаграмма состояний системы Nb-V
Закон Вегарда - эмпирическое правило, которое гласит, что существует линейная зависимость при постоянной температуре между свойствами кристаллической решетки сплава и концентрацией отдельных его элементов.
Таким образом, параметры кристаллической решётки (a) твердого раствора (сплава) материалов с одинаковой структурой решётки, могут быть найдены путем линейной интерполяции <http://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D0%B8%D0%BD%D1%82%D0%B5%D1%80%D0%BF%D0%BE%D0%BB%D1%8F%D1%86%D0%B8%D1%8F> между параметрами решётки исходных соединений.
|
|
|
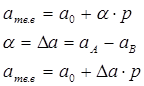
где р - атомная концентрация одного из элементов системы
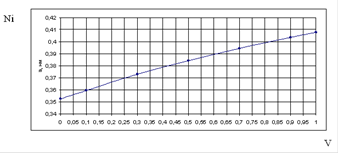
Рисунок 9 - График зависимости периода решетки твердого раствора от состава 1-по правилу Вегарда, 2- по литературным данным
|
|
|
