Глава 3. Оптимизация использования фонда развития

Предприятия.

 

В современных условиях, когда формирование ресурсов на развитие предприятия является заботой самого предприятия, когда средства на обеспечение благополучия в будущем коллектив отделяет в ущерб потреблению сегодня, особую актуальность приобретает задача оптимального, очень разумного использования фонда развития. Задача должна решаться взвешенно, с предварительной оценкой ожидаемого экономического эффекта средств, расходуемых на развитие предприятия. Этому способствует использование модели, которая связывает эффективность фонда развития с распределением его по разным вариантам и с продолжительностью «инкубационных периодов» выбранных вариантов вложения средств.

Данная модель основывается на следующих рассуждениях. Предприятие располагает фондом развития в объеме F_po. Этот фонд может обеспечить разный прирост прибыли D Р в зависимости от вариантов его использования. Варианты различаются эффективностью вложений m _i — тем, что дает каждый вложенный рубль в единицу времени, и продолжительностью «инкубационного периода» t _i. Величина прироста D Р зависит, помимо направлений инвестирования, от отрезка времени t, за который она оценивается, т.е. D P = D P (t). Задача состоит в таком выборе объемов Fp_i, вложений по каждому i -му варианту, при котором обеспечивается требуемое значение D P тр прироста D P (t). Таким образом F_po надо распределить так, чтобы D P (t) ³ D P тр.

Примем, что эффективность вложений m_i в общем случае является функцией времени х вида

 

m _i (х)= a_i + b_i  х + c_i х²,                                                      (1)

где a_i ³0, b_i ³0, a c_i может быть как положительной, так и отрицательной величиной.t-продолжительность времени выбирается с условием t > t _{max .}

Прирост прибыли D P_i (t) предприятия от вложений в i -й вариант определяется по формуле 

                                (2)

 

Общий прирост D P ₀ (t) по всем трем вариантам суммируется, т.е.

                                    (3)

Используя соотношение (2), запишем

.

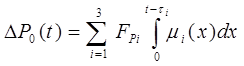Обозначим

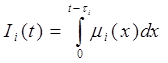,                                    (4) 

тогда

,                     (5)

 по условию

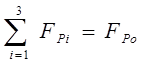                                        (6)

Эффективность использования фонда развития обычно оценивают в относительных единицах

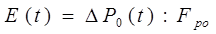                         (7)

т.е. представляют ее как прибыль за время t, полученную с каждого вложенного рубля.

Тогда объемы вложений по вариантам целесообразно также выражать в виде отношений

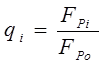                             .                                                   (8)

Теперь на основании (5) и (8) соотношение (7) можно записать так:

 

;                                  (9)

условие (6) примет вид

 .                                                       (10)

Задача ставится так: надо найти значения q ₁, q ₂, q ₃, такие, которые обеспечивают

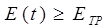                                                                             (11)

и при этом

                                                                                                                                 (12)

 

Здесь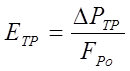
– требуемая эффективность использования фонда развития предприятия.

Условие (11) можно, используя (9), переписать так:

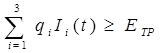.                                 (13)

Оно может выполняться при различных сочетаниях значений q _{1 ,} q ₂, q ₃, т.е. условия (11) и (12) не обеспечивают определенности решения задачи. Для этого нужно ввести дополнительное условие. Будем полагать, что поступим наименее предвзято при определении q _{1 ,} q ₂, q ₃, удовлетворяющих условиям (11) и (12), если их возможным значениям придадим максимальную неопределенность.

В качестве меры неопределенности используем энтропию совокупности значений q _{1 ,} q ₂, q ₃, которая может быть записана так [3]:

          

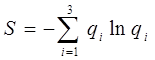
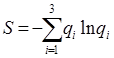
(Числа q_i  меньше единицы, их логарифмы отрицательны и знак минус перед суммой поставлен для того, чтобы энтропия была положительной).

Теперь задача ставится так:

Найти такие q _{1 ,} q ₂, q ₃, при которых

                            (14)

и выполняются условия  

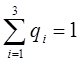,                                                    (15) 

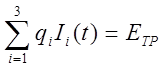.                                  (16)

Здесь условие (13) заменено на знак равенства для обеспечения однозначности. Задача может быть решена известным в математике методом неопределенных множителей Лагранжа. Согласно этому методу на основании (14)-(16) составляется функция

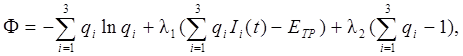
где λ₁ и λ₂ являются множителями Лагранжа.

Затем определяют частные производные по q_i, λ₁ и λ₂, которые приравнивают к нулю, т.е.

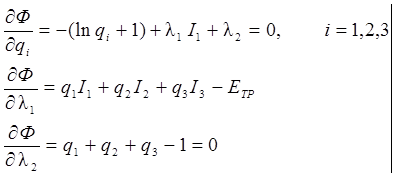       (17)

Система (17) состоит из 5 уравнений с 5 неизвестными q _{1 ,} q ₂, q ₃, λ₁, λ_2. Решение системы уравнений (17) может быть получено с использованием стандартных математических пакетов программ. Также решение системы (17) можно получить, преобразовав ее к более простому виду.

Первые 3 уравнения могут быть переписаны так:

.

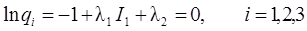Отсюда

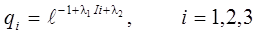  .                                    (18)

 

Подставим q_i в предпоследнее и последнее уравнения системы (17), получим

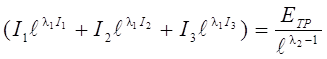 ;                                   (19)

       .                                (20)

Поделим левую и правую части (19) на левую и правую части (20):

    .                   (21)

Если задаться требуемой эффективностью E_TP  использования фонда развития, то (21) будет представлять собой уравнение с одним неизвестным λ_1.

Упростим соотношение (21), с этой целью проинтегрируем правую и левую части по λ_1,

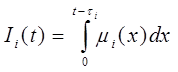получим   

 ,

,

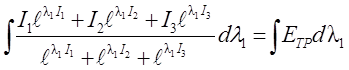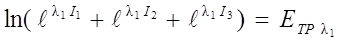отсюда 

.

Обозначим 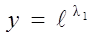и запишем

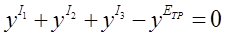.                            (22)

Для решения (22) имеется стандартная математическая программа. Ею можно воспользоваться в дисплейном классе.

Вводимые в компьютер параметры I ₁, I ₂, I ₃ вычисляются по формулам (1) и (4) на основе полученных студентом исходных данных (приложение А).

После вычисления l ₁, необходимо определить сумму А = ,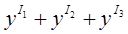

затем преобразовать (20) к виду 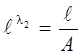 , отсюда

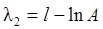.                                                      (23)

Теперь искомые q ₁, q ₂, q ₃ могут быть определены по формулам (18).

Отсутствие ошибок в вычислениях надо проверить по признаку выполнения равенства (15).

 

Fp, руб

t1, дни

t2, дни

t3, дни

a1

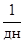
b1

c1

a2

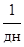
b2

c2

a3

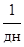
b3

c3

ETP

1,0×106

46

115

60

0

1,2×10-2

1,26×10-4

0,51

0,46×10-2

-0,22×10-4

0,31

0

0

1,16

 

μ₁=0,012x+0,000126x²;

μ₂=0,51+0,0046x-0,000022x²;

μ₃=0,31

 

 

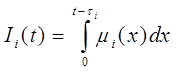
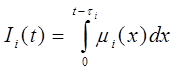
По формуле                                

Определим неизвестные значения I_i:

I ₁ (t) =606, 262;

I ₂ (t) = - 6 9, 66;

I 3(t)= 38

Подставим значения I_i в уравнение 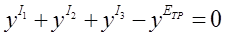  и решим его графическим способом с помощью прикладного пакета MathCAD. Получим:

Y=0,99228

Определим сумму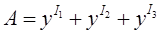

А=0,99228^606,262+0,99228^-69,66+0,99228³⁸=0,99862

λ1=1-lnA=1.007

l=0.999

λ2=l-lnA

λ2=1.11049

 

 

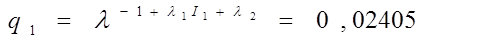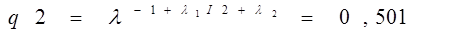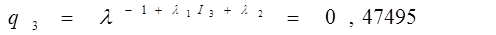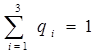
0.02405+0,501+0,47495=1

Отсюда найдем 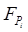- объемы вложений по каждому варианту:

 

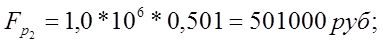
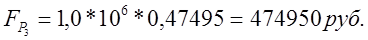
Заключение.

 

В данной курсовой работе была описана организационная структура ООО «Метра», которая является линейной и имеет четыре уровня управления. В результате проделанной работы были углублены знания, полученные в результате изучения курса “Теория управления”, изучение методов разработки экономико-математических моделей управления развитием предприятия. Помимо этого получены дополнительные знания в пакете математических программ MathCAD, закреплены навыки работы с экономической литературой, компьютерными технологиями.

В каждом разделе были подробно изложены назначения каждой подсистемы управления, охарактеризована система управления развитием предприятием как замкнутая система управления с «обратной связью», изложено содержание объекта управления, перечислены параметры, по которым оценивается его состояние, а также указаны причины, вызывающие отклонение параметров от нормы и пути воздействия на состояние объекта управления.

 

 

Список использованной литературы.

1. Годовой отчёт ООО «Метра» за 2005 год.

2. Управление организацией: Учебник / Под ред. А.Г. Поршнева, З.П. Румянцева-М: ИНФРА-М, 2002.-669 С.

3. Основы менеджмента / Мескон М.Х., Альберт М.-М., 1992.-702 С.

4. Теория организации: УЧЕБНИК ДЛЯ ВУЗОВ / г.р. Латфуллин, А.В. Райченко. –Питер, 2003.-400с.

5. Теория организации Мильнер Б.З.-М.:ИНФРА-М, 2005.-648 с.

12	Поделиться:

Воспользуйтесь поиском по сайту: