 |
Найти координаты векторов.
|
|
|
|
Понятие вектора. Свободный вектор.
Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:

В данном случае началом отрезка является точка А, концом отрезка – точка В. Сам вектор обозначен через 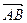 . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор
. Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор 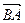 , и это уже совершенно другой вектор.
, и это уже совершенно другой вектор.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором  . У такого вектора конец и начало совпадают.
. У такого вектора конец и начало совпадают.
!!! Примечание: Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.
1) Векторы можно записать двумя большими латинскими буквами: 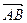 ,
,  ,
, 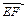 ,… и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
,… и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
2) Векторы также записывают маленькими латинскими буквами:  ,
, 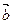 ,
, 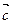 ,… Длиной или модулем ненулевого вектора
,… Длиной или модулем ненулевого вектора 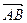 называется длина отрезка АВ. Длина нулевого вектора
называется длина отрезка АВ. Длина нулевого вектора  равна нулю. Длина вектора обозначается знаком модуля:
равна нулю. Длина вектора обозначается знаком модуля:
Вектор можно отложить от любой точки:

И так, свободный вектор – это множество одинаковых направленных отрезков; подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.
Действия с векторами. Коллинеарность векторов.
Правило сложения векторов по правилу треугольников.
Рассмотрим два произвольных ненулевых вектора  и
и 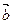 :
:
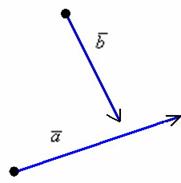
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 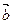 от конца вектора
от конца вектора  :
:

|
|
|
Кстати, если вектор 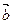 отложить от начала вектора
отложить от начала вектора  , то получится эквивалентное правило параллелограмма сложения векторов.
, то получится эквивалентное правило параллелограмма сложения векторов.
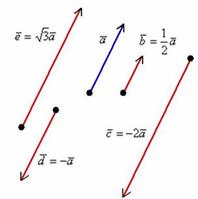
Умножение вектора на число.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленнымии и обозначаются 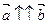 .
.
Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены и обозначаются 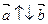
Произведением ненулевого вектора  на число
на число 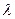 является такой вектор
является такой вектор 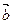 , длина которого равна
, длина которого равна  , причём векторы
, причём векторы  и
и 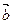 сонаправлены при
сонаправлены при 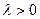 и противоположно направлены при
и противоположно направлены при 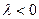 .
.
Правило умножения вектора на число легче понять с помощью рисунка:
Равенство векторов.
Два вектора равны, если они сонаправлены и имеют одинаковую длину.
Координаты вектора на плоскости и в пространстве.
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы 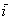 и
и 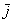 :
:
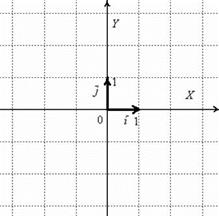
Единичные векторы  и
и 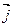 ортогональны (перпендикулярны). Обозначение: ортогональность векторов записывают значком перпендикулярности
ортогональны (перпендикулярны). Обозначение: ортогональность векторов записывают значком перпендикулярности 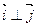 .
.
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости.
Разложение вектора  по базису
по базису 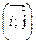 :
: 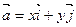
Координаты вектора: 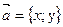
Найти координаты векторов.
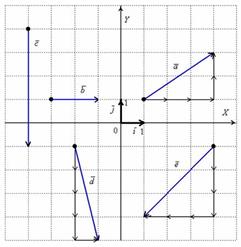
1. 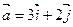 ,
, 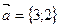 2.
2. 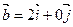 ,
,  3.
3.  ,
, 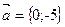 4.
4. 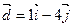 ,
, 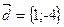 5.
5. 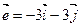 ,
, 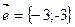
Векторы в пространстве.
Рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата.
Единичные векторы  ,
, 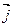 и
и 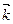 ортогональны (перпендикулярны). Обозначение: ортогональность векторов записывают значком перпендикулярности
ортогональны (перпендикулярны). Обозначение: ортогональность векторов записывают значком перпендикулярности 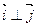 ,
, 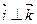 ,
, 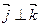
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис в пространстве.
|
|
|
Базисные векторы записываются следующим образом: 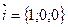 ,
,  ,
, 
Разложение вектора  по базису
по базису  : радиус-вектор
: радиус-вектор 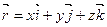 ,
, 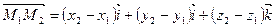
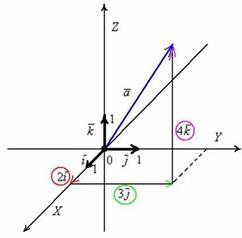
Координаты вектора: 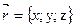 ,
, 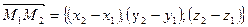

Длина вектора (модуль): 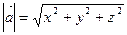 ,
,
расстояние между двумя точками: 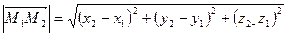
Действия над векторами.
Даны два вектора: 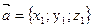 и
и 
1. Сумма векторов: 
2. Разность векторов: 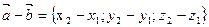
3. Умножение вектора на число 
4. Скалярное произведение векторов: 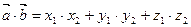
5. Условие коллинеарности векторов: соответствующие координаты пропорциональны

6. Угол между векторами  и
и 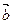 , точнее его косинус:
, точнее его косинус: 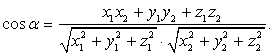
7. Условие перпендикулярности векторов: скалярное произведение векторов равно нулю. 
8. Векторное произведение векторов: 


9. где S — площадь параллелограмма, построенного на векторах  и
и 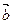 :
: 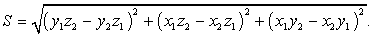
10. Смешанное произведение векторов  ,
, 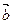 и
и 

11. Условие компланарности трех векторов (принадлежат плоскости или параллельны ей), если смешанное произведение равно нулю.
.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е. 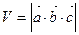
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор  – запишем
– запишем  ;
;
вектор  – запишем
– запишем  ;
;
вектор  – запишем
– запишем 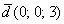 .
.
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах.
Пример 1. Даны две точки плоскости 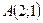 и
и 
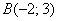 . Найти координаты вектора
. Найти координаты вектора 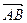
Решение: по соответствующей формуле: 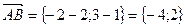
Ответ: 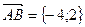
Пример 2. Это примеры для самостоятельного решения.
а) Даны точки  и
и 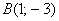 . Найти векторы
. Найти векторы 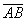 и
и  .
.
б) Даны точки  и
и  . Найти векторы
. Найти векторы  и
и 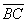 .
.
в) Даны точки 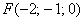 и
и  . Найти векторы
. Найти векторы  и
и 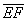 .
.
г) Даны точки 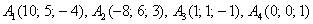 . Найти векторы
. Найти векторы  .
.
Пример 3. Даны точки 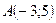 и
и 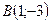 . Найти длину отрезка АВ.
. Найти длину отрезка АВ.
Решение: по соответствующей формуле:

Ответ: 
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки  и
и 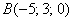 . Найти длину отрезка
. Найти длину отрезка 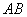 .
.
Пример 5.
а) Даны точки 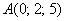 и
и  . Найти длину вектора
. Найти длину вектора  .
.
б) Даны векторы 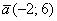 ,
, 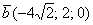 ,
,  и
и 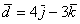 . Найти их длины.
. Найти их длины.
Пример 6.
Даны векторы 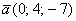 и
и 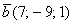 . Найти
. Найти 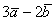 и
и 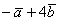
Решение: Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
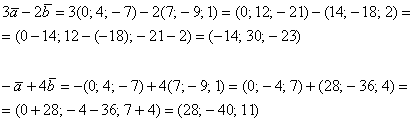
Ответ: 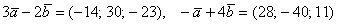
Пример 7. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов даны, подставляем их в формулу 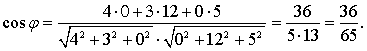 Ответ: 36/65.
Ответ: 36/65.
|
|
|
Пример 8.
Вычислить площадь треугольника с вершинами А(1;-1;2), В (5;-6;2), С(1;3;-1).
Решение.
 ,
, 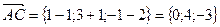
тогда площадь треугольника АВС будет вычисляться следующим образом:
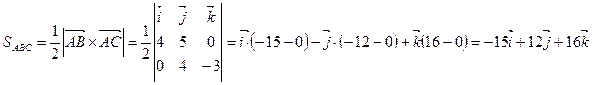
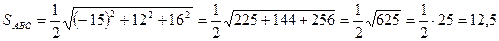 (кв. ед.)
(кв. ед.)
Ответ: 12,5.
Пример 9. Вычислить смешанное произведение векторов 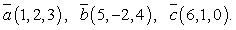
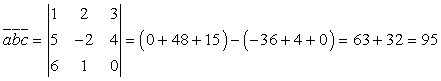 Ответ: 95.
Ответ: 95.
|
|
|


