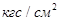Главная | Обратная связь | Поможем написать вашу работу!

Материальный баланс процесса выпаривания

Основные уравнения материального баланса:

(3.1)

(3.2)

где , - соответственно массовые расходы начального и конечного раствора, кг/с;

, - соответственно массовые доли растворенного вещества в начальном и конечном растворе;

W – массовый расход выпариваемой воды, кг/с.

Из формулы 3.2 получаем:

;

кг/с.

Решая совместно уравнения 3.1 и 3.2 получаем:

;

кг/с.

Материальный баланс выпаривания

Таблица 3.1

Поток	Обозначение	Численное значение, кг/с	Содержание соли, массовые доли
Исходный раствор		4,58	0,12
Упаренный раствор		2,2	0,25
Вторичный пар	W	2,38	-

Определение температур и давлений в узловых

Точках технологической схемы

3.2.1 Определение температуры конденсации и давления вторичного пара в барометрическом конденсаторе

Температуру конденсации вторичного пара в барометрическом конденсаторе мы определяем по формуле:

(3.3)

где - температура конденсации греющего пара, ;

- полезная разность температур, К.

Принимаем = 40 К.

- температурная депрессия, К;

- гидростатическая депрессия, К.

Принимаем = 5 К.

- гидравлическая депрессия, К.

Принимаем = 1 К.

Давление греющего пара:

где - атмосферное давление,

- избыточное давление греющего пара.

По, находим по (/1/, табл. LVII,стр. 549) температуру греющего пара :

полагаем равной при и . По (/1/, рис. XIX, стр. 568), находим :

Подставляя, найденные значения и в уравнение для получаем:

По (/1/, табл. LVI, стр. 548) находим, что при . По (/1/, табл. LVII, стр. 549) находим температуру в барометрическом конденсаторе при давлении :

3.2.2 Определение температур и давлений в выпарном аппарате

Температура в сепараторе :

;

По [1, табл. LVI] находим давление вторичного пара в сепараторе при температуре :

Температура кипения раствора в сепараторе выпарного аппарата, при которой конечный раствор выводится из аппарата определяется по формуле: См. приложение.

; (3.4)

где 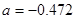, , - давление, Па.

Уточненное значение температурной депрессии определяем по формуле:

;

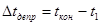Оптимальная высота уровня по водомерному стеклу определяем по формуле:

(3.5)

где и - соответственно плотности раствора конечной концентрации и воды при средней температуре кипения , . Так как не известно, то принимаем . - рабочая высота труб, принимаем Плотность воды можно рассчитываем по формуле:

(3.6)

Плотность раствора определяем по формуле:

(3.7)

где , , .

Откуда

Подставляя найденные значения и в формулу 3.5 получаем:

Гидростатическое давление в середине высоты труб при определяем по формуле:

(3.8)

Подставляя в формулу 3.4 давление , находим среднюю температуру кипения раствора:

Находим уточненное значение гидростатической депрессии :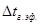

Находим уточненное значение полезной разности температур :

Начальную температуру раствора принимаем равной .

Таблица 3.2 - Температурный режим работы выпарной установки

Узловые точки технологической схемы	Температура,		Давление,
Барометрический конденсатор		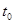90		0.715
Паровое пространство аппарата		91		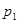0.740
Выход кипящего раствора в сепаратор		98.57	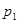в сепараторе	0.740
Трубное пространство (середина высоты труб)		99.48		0.801
Межтрубное пространство греющей камеры		142,9		4,03
Вход исходного раствора в выпарной аппарат		92,0	-	-

3.3 Тепловой баланс выпарного аппарата

3.3.1 Расход теплоты на выпаривание

Тепловая нагрузка выпарного аппарата равна:

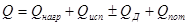, (3.9)

где 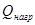- расход теплоты на нагревание раствора, кВт; - расход теплоты на испарение влаги кВт; - теплота дегидратации. Обычно, эта величина мала по сравнению с другими статьями теплового баланса и ею можно пренебречь; - расход теплоты на компенсацию потерь в окружающую среду.

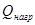Расход теплоты на нагревание раствора , определяется по формуле:

, (3.10)

где - теплоемкость разбавленного раствора, определяется по формуле:

(3.11)

где 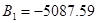, , , , - удельная теплоемкость воды, определяется по формуле:

(3.12)

где - температура воды,

Тогда по формуле 3.11 будет равна:

и по формуле 3.10 получим:

Расход теплоты на испарение определяется по формуле:

(3.13)

где - энтальпия вторичного пара, 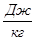при температуре .

По (/1/, табл. LVI, стр. 548) находим :

Теплоемкость воды по формуле 3.12 при температуре будет равна:

тогда по формуле 3.13 находим расход теплоты на испарение:

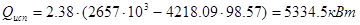Расход теплоты на компенсацию потерь в окружающую среду ,при расчете выпарных аппаратов принимают 3-5% от суммы . Таким образом, равняется:

Следовательно, количество теплоты, передаваемой от греющего пара к кипящему раствору, по формуле 3.9 равняется:

3.3.2 Определение расхода греющего пара

Расход греющего пара (в кг/с) в выпарном аппарате определяем по уравнению:

, (3.14)

где - паросодержание (степень сухости) греющего пара; 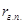- удельная теплота конденсации греющего пара, . Из (/1/, табл. LVII, стр. 550) находим для температуры ,

И получаем:

Удельный расход греющего пара:

3.4 Расчет греющей камеры выпарного аппарата

Выпарная установка работает при кипении раствора в трубах при оптимальном уровне. При расчете выпарного аппарата мы приняли высоту труб 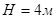. При расчете установки мы приняли: тепловая нагрузка ; средняя температура кипения раствора хлорида аммония ; температура конденсации сухого насыщенного водяного пара . Для кипящего раствора коэффициент теплопроводности раствора NH 4 Cl мы рассчитываем по формуле:

, (3.15)

где , 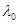- коэффициент теплопроводности воды, :

, (3.16)

Тогда по формуле 2.15 получаем:

Средняя разность температур:

Находим коэффициент теплоотдачи от конденсирующегося водяного пара к поверхности вертикальных труб по формуле:

, (3.17)

где (/1/, табл. 4.6, стр. 162).

;

Следовательно,

Коэффициент теплоотдачи от стенки труб к кипящему раствору:

, (3.18)

где

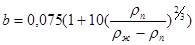, (3.19)

и - соответственно плотности раствора и его пара при средней температуре кипения , К; - динамический коэффициент вязкости, ; 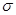- поверхностное натяжение раствора, Н/м, при и .

Плотность раствора, рассчитанная по формулам 3.6 и 3.7, равна:

;

Плотность пара находим по (/1/, табл. LVI, стр. 548):

Таким образом, по формуле 3.19 получаем:

Динамический коэффициент вязкости рассчитывается по формуле:

, (3.20)

где 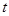- температура раствора, 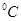, , , ; - вязкость воды, :

(3.21)

При средней температуре кипения раствора получаем:

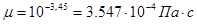Поверхностное натяжение берем по (/1/, табл. XXIII, стр. 526) для хлорида аммония 10% концентрации:

Подставляя найденные значения в формулу 3.18 получаем:

Принимаем тепловую проводимость загрязнений (/1/, табл. XXXI, стр. 531) стенки со стороны греющего пара и со стороны кипящего раствора . Коэффициент теплопроводности стали по (/1/, табл. XXVIII, стр. 529) принимаем равным:

по (/3/, табл. 2.2, стр. 16) толщину труб принимаем равной 2 мм. Тогда

Ввиду того, что и 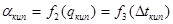, для расчета коэффициента теплопередачи принимаем метод последовательных приближений.

Для определения исходного значения , учитывая: что при установившемся режиме теплопередачи , выражаем через :

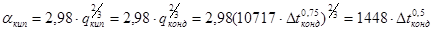Затем рассчитываем исходные значения и , принимая :

;

Находим значение

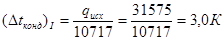Составляем расчетную таблицу 3.3, в которую записываем исходные данные 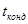, , , и результаты последующих расчетов.

Таблица 3.3 Температурный режим работы выпарной установки

Прибли-жения и провероч-ный расчет	Конденсация греющего пара

I	142,9	139,9		3,0		7529		24770
II	142,9	137,31		5,59		6594		36863
III	142,9	136,06		6,85		6267		42934
IV	142,9	135.17		7.73		6081		47008
Прибли-жения и провероч-ный расчет	Стенка и ее загрязнения	Кипение раствора

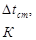
I	1785	13,88	125,73		109,9	28,65	2532		72548
II	1785	20,65	116,66		109,9	19,58	3301		64628
III	1785	24,05	112,01		109,9	14,93	3654		54552
IV	1785	26.33	108.84		109,9	11.76	3881		45646

I. Первое приближение:

;

; .

В первом приближении: .

II. Второе приближение.

Рассчитываем по первому приближению :

тогда

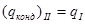Величину определяем, принимая при

Затем выполняем аналогичный расчет (см. строку II в табл. 3.3).

Расхождение и 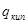по второму расчету:

III. Третье приближение.

Рассчитываем по второму приближению :

тогда

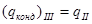Величину определяем, принимая при :

Затем выполняем аналогичный расчет (см. строку III в табл. 3.3).

Расхождение и по третьему расчету: .

По результатам расчетов второго и третьего приближения строим график . Полагая что при малых изменениях температуры поверхностные плотности и линейно зависят от , графически определяем Графическая зависимость

IV. Проверочный расчет (см. табл. 3.3).

Расчеты аналогичны расчетам первого приближения.

Расхождение и :

По данным последнего приближения определяем коэффициент теплопередачи:

Площадь поверхности теплопередачи:

По (Таблице 2.2 стр. 16) принимаем аппарат Тип 1, Исполнение 2, группа А (С выносной греющей камерой и кипением в трубах), с площадью поверхности теплопередачи 132 (действительная), Трубы 38 х 2 мм, длинной Н = 4000 мм, т.е. с запасом .

3.5 Полный тепловой расчет подогревателя начального раствора

3.5.1 Ориентировочный расчет теплообменного аппарата для подогрева раствора перед подачей в выпарной аппарат

Таблица 3.4 - Основные данные для расчета подогревателя

Раствор хлорида аммония			Греющий пар
, % масс.
12	23	92,0	142,9	4,03

Значение усредненной по всей теплообменной поверхности разности температур рассчитывается по формуле:

; (3.22)

при этом

;

Получаем

Средняя температура раствора :

где - среднее арифметическое значение температуры теплоносителя, которое изменяется на меньшую величину (в данном случае температура конденсации греющего пара);

Расход раствора :

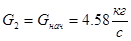Расход теплоты на нагрев раствора:

, (3.23)

где - удельная теплоемкость раствора, рассчитанная по формуле 2.11, при и % масс.

По формуле 3.12 удельная теплоемкость воды при равна:

Тогда по формуле 3.11 получаем:

Расход теплоты на нагрев раствора по формуле 3.23 равен:

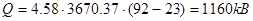Расход греющего пара:

Принимая по (/1/, табл. 4.8 стр. 172) ориентировочный коэффициент теплопередачи , (аппарат со свободной циркуляцией, передача тепла от конденсирующегося пара к воде), рассчитываем ориентировочную поверхность теплопередачи:

Проходное сечение трубного пространства рассчитываем по формуле:

, (3.24)

где - внутренний диаметр труб; - динамический коэффициент вязкости начального раствора при средней температуре ; Re – критерий Рейнольдса.

По формуле 3.21 при для воды получаем:

а по формуле 3.20 для раствора находим:

Для обеспечения интенсивного теплообмена подбираем аппарат с турбулентным режимом течения теплоносителей. Раствор направляется в трубное пространство, греющий пар – в межтрубное.

Максимальное проходное сечение считаем при критерии Рейнольдса :

минимальное – при :

По полученному оценочному значению поверхности теплопередачи 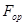с учетом и , в качестве подогревателя, мы выбираем по (/3/ табл. 1.2 стр. 6) 2-у ходовый теплообменник, с внутренним диаметром кожуха 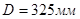, числом труб , поверхностью теплообмена 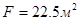, длиной труб , проходным сечением и числом рядов труб , расположенных в шахматном порядке.

3.5.2 Подробный расчет теплообменного аппарата

3.5.2.1 Теплоотдача в трубах

Находим, что теплоотдача для раствора описывается уравнением:

, (3.25)

где - критерий Нуссельта; - поправочный коэффициент; Re – критерий Рейнольдса; Pr – критерий Прандтля; 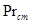- критерий Прандтля при температуре стенки трубы.

Коэффициент примем равным 1, полагая, что (/1/, табл. 4.3, стр. 153), где - длина труб, - эквивалентный диаметр. Критерий Рейнольдса рассчитываем по формуле:

, (3.26)

где 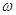- средняя скорость потока, и - соответственно плотность раствора и динамический коэффициент вязкости, при средней температуре .

По формуле 3.7 плотность раствора при и % масс. равняется:

Среднюю скорость потока определяем по формуле:

Учитывая, что для труб круглого сечения диаметр труб и эквивалентный диаметр совпадают, то для труб 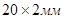получаем:

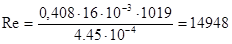Критерий Прандтля находим по формуле:

, (3.27)

где - удельная теплоемкость, ; - коэффициент теплопроводности, ; - динамический коэффициент вязкости, .

Коэффициент теплопроводности при 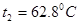и % масс. по формуле 3.15 равняется:

Таким образом, критерий Pr при и равняется:

Коэффициент теплоотдачи от раствора к стенке:

С учетом формулы 3.25 получаем:

, (3.28)

3.5.2.2 Теплоотдача при пленочной конденсации водяного пара

Для водяного пара в случае конденсации на пучке горизонтальных труб осредненный по всему пучку коэффициент теплопередачи можно рассчитать по формуле:

, (3.29)

где - поправочный множитель, учитывающий влияние числа труб по вертикали; - наружный диаметр труб; =7430 (взято из /1/, табл.4.6, стр. 162 при температуре конденсации греющего пара); - разность средней температуры конденсации греющего пара и температуры стенки со стороны греющего пара :