Изучение колец ньютона. Определение радиуса кривизны линзы

ИНТЕРФЕРЕНЦИЯ СВЕТА.

Интерференцией волн называется явление усиления колебаний в одних точках пространства и ослабления колебаний в других точках в результате наложения двух или нескольких когерентных волн, приходящих в эти точки.

Поскольку свет представляет собой электромагнитные волны, должна наблюдаться интерференция света

Когерентные волны. Волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся со временем, называются когерентными (связанными).

Оптическая длина пути. Если после разделения пучка света на два пучка последние будут распространяться в различных средах, то при подсчете приобретаемой волнами разности фаз следует учитывать изменение длины волны при переходе из вакуума в среду.

Оптической длиной пути называется произведение коэффициента преломления n на геометрическую длину пути d.

Разность фаз когерентных волн. Если в вакууме длина волны , то в среде с коэффициентом преломления п длина волны и скорость распространения волны .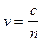

Если одна из волн проходит путь d₁ в среде с коэффициентом преломления n₁, а другая – путь d₂ в среде с коэффициентом преломления n₂, то приобретаемая разность фаз

Для наблюдения устойчивой во времени интерференционной картины необходимы условия, при которых частоты, поляризации и разность фаз интерферирующих лучей были бы постоянными в течение всего времени наблюдения.

Для получения когерентных волн, очевидно, необходимо иметь два источника волн одинаковой частоты, колеблющихся с постоянной разностью фаз. Однако световые волны, испускаемые отдельными атомами источника света, никак не согласованы по фазе. Поэтому когерентные световые волны получают, разделяя при помощи того или иного оптического устройства, волну, идущую от одного источника света, на две волны, идущие по разным направлениям. Если эти волны пройдут различные пути, а затем будут снова сведены и наложены одна на другую, то, поскольку на путях разной длины фаза волны меняется на разную величину, они придут в точку встречи с постоянной неизменной во времени разностью фаз.

Рассмотрим две волны одинаковой частоты , распространяющиеся в одном направлении. Накладываясь, друг на друга, они возбуждают в некоторых точках пространства колебания одинакового направления:

,

.

Амплитуда результирующего колебания в данной точке определяется, формулой: .

Если разность фаз возбуждаемых колебаний остается постоянной по времени, то волны называются когерентными, а источники таких волн–когерентными источниками. В случае некогерентных волн непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение: и .

Так как интенсивность света 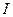~ 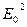, то интенсивность наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности: .

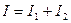В случае когерентных волн имеет постоянное во времени, но разное для каждой точки пространства значение, так что интенсивность:

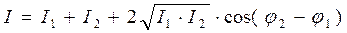, (2.1)

так же постоянна для каждой точки пространства.

Интенсивность света по всему полю, где происходит наложение когерентных волн, будет изменяться в преде лах: , причем в тех точках пространства, для которых > значения 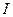> 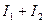, в тех точках, для которых < , 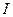< 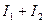. Таким образом, при наложении двух и более когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают устойчивые максимумы, в других минимумы интенсивности. Это явление и есть интерференция световых волн.

Особенно отчетливое проявление интерференции света наблюдается в том случае, когда интенсивность интерферирующих волн одинакова: . Согласно (2.1) в этом случае:

, (2.2)

в минимумах , в максимумах 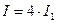. Для некогерентных волн при этом же условии получается всюду одинаковая интенсивность .

Пусть и 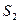(рис.1)– когерентные источники. Расстояние между источниками 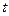мало по сравнению с расстоянием 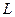до экрана Э, помещенного параллельно линии, соединяющей источники. Характер интерференционной картины на экране зависит от разности фаз , которую интерферирующие волны имеют в точке наблюдения . Эта разность фаз, в свою очередь, обусловлена тем, что волны от источников и 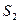до точки проходят разные пути и . Разность путей (разность хода лучей) связана с разностью фаз , соотношением:

. (2.3)

Теперь (2.2) с учетом (2.3) можно записать в виде:

.

Интенсивность в точке будет 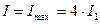, если выполняется условие: , или , (2.4) и, если , или , (2.5)где – любое целое число.

Условия (2.4) и (2.5) называются условиями интерференционного максимума и минимума соответственно.

В точке будет находиться центральная светлая полоса (разность хода равна 0). Расстояние от него до -ой светлой полосы определяется из условия: .

Положение темных полос определяется условием: .

Расстояние между соседними светлыми (темными) полосами есть: , откуда . (2.6)

 

Зеркала Френеля. В качестве двух когерентных источников света Френель использовал изображения одного источника в двух плоских зеркалах, расположенных под углом, близким к 180°. Результат интерференции лучей, отраженных от этих зеркал, определяется разностью хода лучей от источника S (или от его мнимых изображений в зеркалах) до точки встречи (рис. 2):

 

S₁M-S₂M=2(k+1) 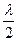– условие минимума;

S₁M - S₂M=k 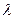– условие максимума; k=0, 1, 2, …

Бипризма Френеля. В бипризме Френеля (рис.3.) для получения когерентных источников света используется преломление света от одного точечного источника в двух призмах с малым преломляющим углом, сложенных основаниями.

После преломления получаются расходящиеся пучки света, которые можно рассматривать как посланные «мнимыми» источниками S₁ и S₂:

S₁M-S₂M=k 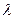– условие максимума;

S₁M-S₂M = (2k+1) 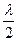– условие минимума при интерференции.

Зеркало Ллойда. В зеркале Ллойда (рис.4) прямой пучок света от источника S интерферирует с пучком света, отраженным от плоского

 

зеркала. Когерентными источниками являются источник света S и его мнимое изображение S, в зеркале.

Билинза Бийе. В билинзе Бийе (рис.5) когерентные волны получаются посредством преломления пучка света от источника в двух половинах разрезанной линзы, незначительно сдвинутых одна относительно другой.

 

 

Щели Юнга. В отличие от описанных выше устройств щели Юнга (рис. 6.) используют для получения интерференционной картины дифракции света. Свет, проходящий через узкую щель, дифрагирует, отклоняется от первоначального направления.

При этом части одной и той же волны, вышедшей из щели в первом экране и прошедшие разные щели во втором экране, перекрываются и интерферируют.

 

Интерферометр Жамена (рис. 7) состоит из двух плоскопараллельных стеклянных пластин. Если пластины строго параллельны, то лучи, встречающиеся в точке F, не приобретают разности хода. При использовании несколько расходящегося пучка света наблюдаются полосы равного наклона.

Если на пути одного из лучей АВ или EF поместить прозрачную среду с другим коэффициентом преломления, то лучи АВ и EF приобретут разность хода l(n₂-n₁),где l—длина внесенного слоя, n₂ — коэффициент преломления внесенной среды, n₁ – коэффициент преломления воздуха.

Рис. 7 Рис. 8

Если разность хода в длинах волн 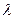используемого света равна , то интерференционная картина смещается на т полос. Смещение на 1/10, полосы уже легко заметить. Интерферометр Жамена, используемый таким образом для определения коэффициентов преломления, является интерференционным рефрактометром.

Интерферометр Майкельсона (рис.8) служит для точного измерения длин. Луч света, попадая в интерферометр посредством полупрозрачной пластинки, покрытой с одной стороны тонким слоем серебра, разделяется на два луча, распространяющиеся во взаимно перпендикулярных направлениях вдоль плеч интерферометра l ₁ и l ₂. После отражения от зеркал М и N лучи вновь падают на полупрозрачную пластинку, от которой (частично) распространяются по линии КС, интерферируя между собой вследствие наличия разности хода 2(l ₁ – l ₂), и направляются в зрительную трубу. На пути луча, отраженного от полупрозрачной пластинки А, помещают прозрачную пластинку Д, сходную с пластинкой А, но не покрытую серебром. Пластинка В является компенсатором, так как при ее отсутствии луч, падающий на зеркало N, прошел бы слой стекла один раз, а луч, падающий на зеркало М, – три раза. В зрительную трубу наблюдаются полосы (части колец) равного наклона. Перемещение зеркала N микрометрическим винтом вдоль луча приводит к перемещению полос. При этом сдвиг зеркала на 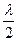меняет разность хода на 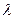и изменяет картину на одну полосу.

 

Интерферометр В. А. Линника. предназначен для исследования качества обработки поверхностей.

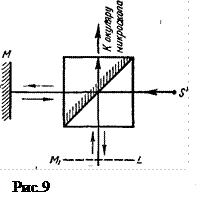
Микроинтерферометр (рис.9) помещается между объективом и окуляром микроскопа, причем роль полупрозрачной пластинки А и компенсатора В в интерферометре Майкельсона здесь играет стеклянный кубик из двух призм, составленных диагональными гранями, одна из которых покрыта полупрозрачным слоем серебра.

Зеркало М c направлением падающих на него лучей образует угол, незначительно отличающийся от 90°. Поэтому плоскость мнимого изображения зеркала М (референтная плоскость M₁) и исследуемая поверхность L образуют тонкий клин. В поле зрения микроскопа наблюдаются интерференционные полосы, параллельные ребру клина. Наличие бугров или впадин в исследуемой поверхности приводит к искривлению полос.

Разрешающая способность интерференционных приборов. Согласно Релею разрешающая способность приборов определяется условием, при котором максимум интенсивности для длины волны 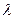и минимум интенсивности для волны длиной совпадали. При этом, по Релею, указанные длины волн считаются разрешенными. Разрешающая способность оценивается величиной , где 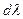— минимальная разность двух длин волн, зависящая от 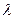, для которой выполнено условие Релея. Для интерференционного спектроскопа:

где т – порядок спектра, N – число интерферирующих пучков света (число щелей решетки).

 

Окуляр -микрометр

Для измерения линейных размеров изображений малых объектов пользуются окуляр -микрометром, который может применяться вместо окуляра микроскопа или самостоятельно как лупа.

окуляр -микрометра (рис.10) находится неподвижная сетка с делениями (шкала) и подвижная прозрачная пластинка с визиром − перекрестие и биштрих (двойной штрих). Перекрестие (и вместе с ним биштрих) перемещается с помощью барабана окуляр - микрометра. Поворот барабана на один оборот соответствует перемещению визира на одно деление окулярной шкалы. Одно деление окулярной шкалы соответствует 1 мм.

Окулярная шкала имеет 8 делений, т.е. перемещение визира от 0 до 8 соответствует 8 мм. Барабан микровинта разбит на 100 делений, т.е. одно деление барабана соответствует 0,01 мм. Например, показание визира на рис. 11 соответствует относительному положению объекта − 3,53 мм.

Для измерения линейных размеров изображений совмещают визир сначала с одной границей изображения, а затем − с другой. При каждом совмещении визира с границей изображения фиксируют показания окулярной шкалы и шкалы барабана, определяющие относительное положение, а затем находят их разность.

Окуляр -микрометр позволяет измерять линейные размеры изображения с точностью до 0,01 мм, при этом, с учетом увеличение оптического прибора, на котором устанавливается окуляр -микрометр, точность отсчета может быть повышена в несколько раз.

 

Лабораторная работа № 3

ИЗУЧЕНИЕ КОЛЕЦ НЬЮТОНА. ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ

 

Цель работы: экспериментальное определение радиуса кривизны линзы.

Приборы и принадлежности: школьный микроскоп, система для наблюдения колец Ньютона, источники света,окуляр -микрометр.

 

Краткая теория

Если плосковыпуклую линзу малой кривизны положить выпуклой поверхностью на хорошо отполированную плоскую стеклянную пластинку, то между линзой и пластинкой образуется воздушная прослойка, утолщающаяся от точки соприкосновения к краям. Если на эту систему падает свет, то части одной и той же световой волны, отраженные от границ воздушной прослойки, будут интерферировать между собой. При этом наблюдается система концентрических радужных (немонохроматический свет) или чередующихся темных и светлых (монохроматический свет) колец. Кольца Ньютона являются классическим примером полос равной толщины. Они наблюдаются и в проходящем и в отраженном свете, причем каждому темному кольцу в отраженном свете соответствует светлое кольцо в проходящем свете. В отраженном свете картина интерференции значительно контрастнее по сравнению с картиной интерференции в проходящем свете.

Кольца Ньютона представляют собой частный случай интерференции в тонких пленках. В этом случае интерферирующие лучи приобретают разность хода в воздушном зазоре между плосковыпуклой линзой радиуса кривизны и плоскопараллельной пластинкой, на которую положена линза (рис. 11).

 

Рис. 11.

 

Картина интерференции представляет собой ряд чередующихся светлых и темных колец при нормальном падении монохроматического света на линзу.

Так как радиусы колец Ньютона, Возникающие при интерференции в системе пластинка -линза, сравнительно малы, то для их наблюдения и измерения применяется микро-скоп с окуляр -микрометром. Установка для получения и наблюдения колец Ньютона в отраженном свете схематично изображено на рис. 12. В осветителе микроскопа свет от источника 1 проходит светофильтр 2, отражается от полупрозрачного зеркала ПЗ и, проходя через объектив микроскопа, параллельным пучком попадает на систему линза -пластинка. В окуляр - микрометре ОК наблюдаем картину интерференции в отраженном свете. Интерференционная картина рассматривается в микроскоп, поэтому кольца Ньютона будут видны в увеличенном виде. Коэффициент увеличения микроскопа в данной работе равен 6, поэтому, определив радиус кольца по шкале и микрометрическому барабану окуляр микро-метра, полученное значение делят на коэффициент увеличения микроскопа, что будет соот-ветствовать истинному (приведенному) радиусу кольца.

Эта система колец – кольца Ньютона. Если поверхность линзы обладает малой кривизной (R величин) – разность хода интерферирующих лучей приблизительно равна:

(2.7)

т. к. BD=DK=t -толщина зазора в месте падения луча.

(2.8)

Из геометрических соображений:

(2.9)

где r _m – радиус m-го кольца.

Запишем условие образования m-го темного кольца:

. (2.10)

Из (3.4) и (3.3) получаем:

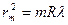. (2.11)

 

По последнему соотношению можно было бы производить расчеты кривизны линзы. Однако на интерференционной картине вместо точки в месте соприкосновения линзы и пластинки образуется темное пятно. Вследствие этого номера измеряемых колец не соответствуют действительным, поэтому расчет R целесообразнее проводить по разности диаметров d_m и d_n

. (2.12)

При обработке результатов измерений удобно также пользоваться графическим методом. Необходимо построить график зависимости r_m² от номера кольца n. Согласно соотношению (2.11) график должен представлять собой прямую линию, проходящую через начало координат, наклон которой равен R.

Порядок выполнения работы

1. Правильно установить микроскоп перед лампой и получить четкую интерференционную картину.

2. Измерить диаметры 3 - 5 темных колец Ньютона, оценить точность измерений. Учитывая, что темное пятно в середине не является кольцом и увеличения микросокопа.

3. Рассчитать радиус кривизны линзы при красном светофильтре l= 650 нм.

4. Повторить опыт с другим светофильтром.

5. Измерить диаметры темных колец Ньютона и по известному радиусу кривизны линзы определить длину волны света.

6. Результаты представить в виде таблицы.

7. Сравнить полученные значения длины волны с табличным и сделать выводы.

Лабораторная работа № 4

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: