 |
Проведение и обработка результатов эксперимента.
|
|
|
|
Каждая строка матрицы – это условия опыта. Для исключения случайных ошибок рекомендуется проводить опыты в случайной последовательности, для чего проводят так называемую рондомизацию (перемешивание), используя таблицы случайных чисел или «жеребьёвку» опытов. С целью взаимной компенсации случайных погрешностей каждый опыт рекомендуется проводить n раз (обычно n = 2…3, редко n = 4…5 раз). Опыты при одних и тех же значениях факторов называют параллельными, а постановку параллельных опытов – дублированием.
Эксперименты могут проводиться по одному из вариантов:
1) с равномерным дублированием опытов,
2) с неравномерным дублированием опытов,
3) без дублирования опытов.
При равномерном дублировании все строки матрицы планирования имеют одинаковое количество параллельных опытов; в случае неравномерного дублирования – неодинаковое. Равномерное дублирование предпочтительно, т.к. даёт простую матрицу и бóльшую точность. Характер дублирования влияет на содержание математической обработки результатов эксперимента.
Методика проведения и обработки результатов экспериментов с равномерным дублированием опытов заключается в следующем.
1) Для каждой строки матрицы планирования по результатам n параллельных опытов находят среднее арифметическое значение параметра оптимизации
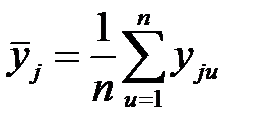 ,
,
где u – номер параллельного опыта,
yju – значение параметра оптимизации в u -м параллельном опыте j -й строки матрицы планирования.
2) С целью оценки отклонений параметра оптимизации от его среднего значения для каждой строки матрицы планирования вычисляют дисперсию  по данным n параллельных опытов и ошибку опыта
по данным n параллельных опытов и ошибку опыта  .
.
 ;
; 
3) Перед началом обработки результатов из параллельных опытов исключают резко выделяющиеся результаты, используя критерий Груббса.
|
|
|
 ;
; 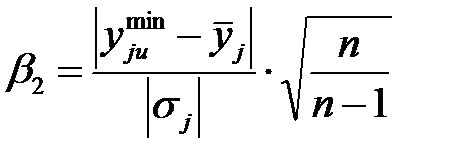 ,
,
где  ,
,  – максимальное и минимальное значение параметра оптимизации в строке матрицы (в n параллельных опытах). Расчетные значения β 1 и β 2 сравнивают с табличным значением βmax. Если β 1 > βmax или β 2 > βmax, то результаты этого опыта исключают. Для сохранения одинакового числа опытов в каждой строке целесообразно провести дополнительные эксперименты, определить новые значения уji, σj, β 1, β 2 и сравнить их с βmax. Эта процедура продолжается до тех пор, пока не будет достигнуто неравенство β 1 < βmax; β 2 < βmax.
– максимальное и минимальное значение параметра оптимизации в строке матрицы (в n параллельных опытах). Расчетные значения β 1 и β 2 сравнивают с табличным значением βmax. Если β 1 > βmax или β 2 > βmax, то результаты этого опыта исключают. Для сохранения одинакового числа опытов в каждой строке целесообразно провести дополнительные эксперименты, определить новые значения уji, σj, β 1, β 2 и сравнить их с βmax. Эта процедура продолжается до тех пор, пока не будет достигнуто неравенство β 1 < βmax; β 2 < βmax.
4) Результаты опытов исследуют на однородность дисперсий по критерию Кохрена, расчетное значение которого определяется по формуле
 .
.
Оно сравнивается с табличным значением Gm. Если Gp < Gm то дисперсии считаются однородными, если Gp > Gm, то дисперсии неоднородны, т.е. исследуемая величина не подчиняется закону нормального распределения. В этом случае нужно попытаться заменить «y» случайной величиной  , достаточно близко подчиняющейся закону нормального распределения.
, достаточно близко подчиняющейся закону нормального распределения.
Для однородных дисперсий опыта вычисляют дисперсию воспроизводимости эксперимента  по выражению
по выражению
 .
.
5) По результатам эксперимента вычисляются коэффициенты математической модели (уравнения регрессии) по следующим формулам, полученным методом наименьших квадратов,
 – свободный член,
– свободный член,
 – коэффициенты уравнения регрессии, характеризующие линейные эффекты взаимодействия,
– коэффициенты уравнения регрессии, характеризующие линейные эффекты взаимодействия,
 – коэффициенты уравнения регрессии, характеризующие двойные эффекты взаимодействия,
– коэффициенты уравнения регрессии, характеризующие двойные эффекты взаимодействия,
 – коэффициенты уравнения регрессии, характеризующие тройные эффекты взаимодействия,
– коэффициенты уравнения регрессии, характеризующие тройные эффекты взаимодействия,
где N – число строк в матрице планирования (число вариантов опытов);
i, l, h – номера факторов;
j – номер строки или опыта в матрице планирования;
yj – значение параметра оптимизации в j-м опыте;
|
|
|
xij, xlj, xhj – кодированное значение (+1 или –1) факторов i, l, h в j-м опыте.
6) Проверяют статистическую значимость коэффициентов уравнения регрессии одним из двух способов:
1) сравнением абсолютной величины коэффициента с его доверительным интервалом,
2) с помощью критерия Стьюдента (αст).
По первому способу для принятого доверительного интервала вычисляют дисперсию и ошибку определения коэффициентов уравнения регрессии по формулам
 ,
, 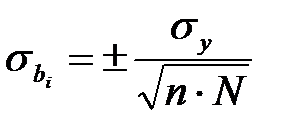 ,
,
где  – ошибка в определении i-го коэффициента уравнения регрессии,
– ошибка в определении i-го коэффициента уравнения регрессии,
 – дисперсия i-го коэффициента уравнения регрессии.
– дисперсия i-го коэффициента уравнения регрессии.
Доверительный интервал 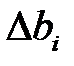 определяется по формуле
определяется по формуле
 ,
,
где  – табличное значение коэффициента Стьюдента при принятом уровне значимости α, а также при числе степеней свободы f, с которой определяется дисперсия
– табличное значение коэффициента Стьюдента при принятом уровне значимости α, а также при числе степеней свободы f, с которой определяется дисперсия  . При равномерном дублировании
. При равномерном дублировании  , где N – количество опытов в матрице планирования, n – количество параллельных опытов в строке. Уровень значимости α обычно принимается равным 0,05 (5%), т.е. доверительная вероятность PD = 0,95 (95%). Коэффициент bi уравнения регрессии считается значимым, если его абсолютная величина больше доверительного интервала, т.е.
, где N – количество опытов в матрице планирования, n – количество параллельных опытов в строке. Уровень значимости α обычно принимается равным 0,05 (5%), т.е. доверительная вероятность PD = 0,95 (95%). Коэффициент bi уравнения регрессии считается значимым, если его абсолютная величина больше доверительного интервала, т.е.
 .
.
При проверке значимости коэффициента bi с помощью критерия Стьюдента вначале определяют расчетное его значение по формуле
 .
.
Затем сравнивают его с табличным значением  для принятого уровня значимости α и числа степеней свободы f. Коэффициент значим, если
для принятого уровня значимости α и числа степеней свободы f. Коэффициент значим, если  . Члены уравнения регрессии со статистически незначимыми коэффициентами исключают из уравнения.
. Члены уравнения регрессии со статистически незначимыми коэффициентами исключают из уравнения.
7) Проверяют гипотезу адекватности найденного уравнения регрессии и результатов эксперимента. Для этого необходимо и достаточно оценить отклонение выходной величины, предсказанное математической моделью  , от результатов эксперимента в точках факторного пространства
, от результатов эксперимента в точках факторного пространства  . Оценка производится по критерию Фишера (F), расчетное значение которого определяется по формуле
. Оценка производится по критерию Фишера (F), расчетное значение которого определяется по формуле
 ,
,
где  – дисперсия адекватности (неадекватности), которая характеризует рассеяние результатов эксперимента вблизи уравнения связи (регрессии), аппроксимирующего искомую функцию.
– дисперсия адекватности (неадекватности), которая характеризует рассеяние результатов эксперимента вблизи уравнения связи (регрессии), аппроксимирующего искомую функцию.
Дисперсия адекватности или остаточная дисперсия определяется по формуле
 ,
,
где K* – количество оставленных коэффициентов уравнения регрессии, включая b0;
|
|
|
 – среднее арифметическое значение параметра оптимизации в j -м опыте;
– среднее арифметическое значение параметра оптимизации в j -м опыте;
 – вычисленное по математической модели значение параметра оптимизации в j-м опыте.
– вычисленное по математической модели значение параметра оптимизации в j-м опыте.
Находят табличное значение критерия Фишера для принятого уровня значимости и соответствующих величин степеней свободы числителя fад и знаменателя fy, которые определяются по формулам
 ;
;  .
.
Если расчетное значение критерия Фишера Fp меньше табличного FT (Fp < FT), то модель адекватна, в противном случае – не адекватна.
Математическая обработка результатов экспериментов с неравномерным дублированием проводится по специальным методикам.
Методика обработки результатов эксперимента, проведенного без дублирования опытов, заключается в следующем. Для вычисления дисперсии воспроизводимости выполняют несколько параллельных опытов (n0) в центре плана (нулевой точке), т.е. все факторы принимаются на нулевых уровнях. По результатам экспериментов вычисляют дисперсию и ошибку опытов
 ;
;  ,
,
где n0 – количество параллельных опытов в нулевой точке;
yu – значение параметра оптимизации в u-м опыте;
 – среднее арифметическое значение параметра оптимизации в n0 параллельных опытах.
– среднее арифметическое значение параметра оптимизации в n0 параллельных опытах.
По результатам экспериментов вычисляются коэффициенты математической модели (уравнения регрессии) по приведенным выше формулам, т.е.
 ;
;  ;
;
 ;
;  .
.
Далее проверяют статистическую значимость коэффициентов уравнения регрессии путем сравнения абсолютного значения коэффициента с его доверительным интервалом или по критерию Стьюдента  . Для этого вычисляют дисперсию и ошибку определения коэффициентов уравнения регрессии по формулам
. Для этого вычисляют дисперсию и ошибку определения коэффициентов уравнения регрессии по формулам
 ,
,  ,
,
где  – ошибка в определении i-го коэффициента уравнения регрессии,
– ошибка в определении i-го коэффициента уравнения регрессии,
 – дисперсия i-го коэффициента уравнения регрессии.
– дисперсия i-го коэффициента уравнения регрессии.
При использовании в качестве оценки доверительного интервала, он определяется по формуле
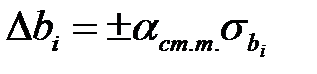 ,
,
где  – табличное значение коэффициента Стьюдента при числе степеней свободы f = n0 – 1 и принятом уровне значимости α (обычно α = 0,05 или PD = 0,95).
– табличное значение коэффициента Стьюдента при числе степеней свободы f = n0 – 1 и принятом уровне значимости α (обычно α = 0,05 или PD = 0,95).
Коэффициенты уравнения регрессии считаются значимыми, если их абсолютная величина больше доверительного интервала, т.е.
|
|
|

При использовании для оценки коэффициента Стьюдента вычисляют их значение по формуле

и сравнивают с табличным значением  при f = n0 – 1 и принятой доверительной вероятности. Если
при f = n0 – 1 и принятой доверительной вероятности. Если  , то коэффициенты статистически значимы, если
, то коэффициенты статистически значимы, если  , то коэффициенты статистически незначимы и соответствующие им слагаемые исключаются из математической модели.
, то коэффициенты статистически незначимы и соответствующие им слагаемые исключаются из математической модели.
Гипотеза адекватности результатов эксперимента и аппроксимирующей их математической модели проверяется по критерию Фишера (F), расчетное значение которого определяется по формуле
 ,
,
где 
K – число переменных (факторов);
 – экспериментальное значение параметра оптимизации в j-м опыте;
– экспериментальное значение параметра оптимизации в j-м опыте;
yj – значение параметра оптимизации в j-м опыте по математической модели;
 – число степеней свободы для линейной модели.
– число степеней свободы для линейной модели.
Для принятого уровня значимости (достоверности) с учетом степени свободы числителя и знаменателя находится табличное значение критерия Фишера (FT). Если Fp < FT, то модель считается адекватной, при Fp > FT – модель неадекватна.
Адекватность модели для интерполяционных экспериментов означает конец решения задачи. Если линейная модель неадекватна, то для интерполяционных экспериментов используют следующие приемы:
1) усложняют линейную модель, вводя эффекты взаимодействия,
2) переходят к планированию 2-го порядка,
3) сокращают интервалы варьирования факторов.
Для экстремальных экспериментов переносят центр плана в лучшую точку и проводят новую серию экспериментов при уменьшенных интервалах варьирования. Причина неадекватности модели может быть не только в интервалах варьирования, но и в том, что нулевая точка находится в непосредственной близости от оптимума. Тогда переходят к планированию 2-го порядка. При этом может оказаться, что уже после построения неполной квадратной модели она станет адекватной.
Если необходимо перейти к натуральным переменным  , нужно вместо хi подставить значения натуральных переменных (т.е. «раскодировать» хi),
, нужно вместо хi подставить значения натуральных переменных (т.е. «раскодировать» хi),
 ,
,
где  – верхнее натуральное значение фактора,
– верхнее натуральное значение фактора,
 – нижнее натуральное значение фактора,
– нижнее натуральное значение фактора,
 – натуральное значение фактора (верхнее или нижнее).
– натуральное значение фактора (верхнее или нижнее).
Пример. Получено уравнение регрессии для расчета шероховатости поверхности Ra при ленточном шлифовании следующего (кодированного) вида:
 ,
,
где x1 – время шлифования (t = 10 с; 60 с),
x2 – сила прижима ленты (Р = 20 н; 70 н),
х3 - зернистость ленты (K =28/20 мкм; 125/100 мкм),
у – шероховатость (Ra), мкм.
Необходимо перейти к натуральным параметрам ( ;
;  ;
;  ;
;  ). Для этого в уравнение регрессии подставим выражения x1, x2, x3, по которым осуществлялось кодирование, и приведем подобные члены.
). Для этого в уравнение регрессии подставим выражения x1, x2, x3, по которым осуществлялось кодирование, и приведем подобные члены.
|
|
|
 ;
;  ;
;
 .
.
Тогда  ,
,
или 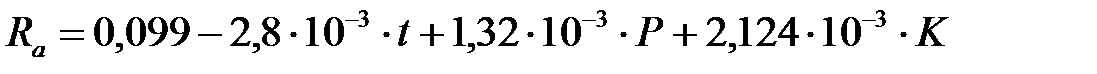 .
.
В ряде случаев для приведения уравнения регрессии к линейному виду целесообразно рассматривать не сами переменные, а некоторые функции этих переменных (логарифмы, обратные величины и др.). Если необходимо получить уравнение регрессии вида
 ,
,
то путем его логарифмирования получим линейное уравнение относительно коэффициентов bi
 .
.
Для нахождения коэффициентов bi пользуются линейным методом наименьших квадратов. Однако следует иметь в виду, что найденные оценки коэффициентов будут смещенными, т.к. в этом случае минимизируется не сумма квадратов отклонений экспериментальных и расчетных значений «yi», а сумма квадратов отклонений логарифмов этих величин.
Пример.
Необходимо установить зависимость стойкости резцов с пластинами Т14К8 от режимов резания. В теории резания эту зависимость принято описывать математической моделью типа
 ,
,
где Т – показатель стойкости (мин),
СТ – постоянный коэффициент,
V – скорость резания (м/мин),
S – подача (мм/об),
t - глубина резания (мм).
После логарифмирования получаем
 .
.
Запишем это уравнение в следующем виде:
 ,
,
где  ;
;  ;
; 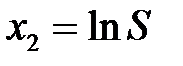 ;
;  ;
; 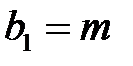 ;
; 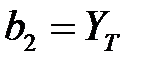 ;
;  ;
;  .
.
Для определения коэффициентов bi можно использовать ПФЭ типа 23. Преобразование независимых переменных 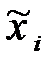 к безразмерным переменным
к безразмерным переменным  производиться с помощью уравнения вида
производиться с помощью уравнения вида
 .
.
Кодирование переменных факторов, матрица планирования и результаты экспериментов представлены в таблицах. Опыт №9 выполнен в центре плана (на нулевом уровне).
Таблица 12
| Уровень факторов | V | S | t | |||

| 
| 
| 
| 
| 
| |
| верхний (+) | 5,42 | 0,2 | -1,61 | 2,0 | 0,69 | |
| нулевой | 4,95 | 0,125 | -2,08 | 1,25 | 0,223 | |
| нижний (–) | 4,02 | 0,050 | -3,0 | 0,5 | -0,69 |
Матрица планирования ПФЭ–23 и результаты эксперимента
Таблица 13
| № опыта, j | xi | Стойкость (Т /ln T), мин | ||||||
| x 0 | x 1 | x 2 | x 3 | Y 1= T 1/ln T1 | Y 2= T 2/ln T2 | Y 3= T 3/ln T3 |  = T j/ln Tj = T j/ln Tj
| |
| + | – | – | – | 162/5,088 | 264/5,576 | 185/5,220 | 203/5,316 | |
| + | + | – | – | 45/3,807 | 78/4,357 | 40/3,689 | 54,3/3,995 | |
| + | – | + | – | 143/4,963 | 215/5,371 | 170/5,136 | 176/5,17 | |
| + | + | + | – | 14/2,639 | 16/2,773 | 22/3,091 | 17,3/2,851 | |
| + | – | – | + | 95/4,554 | 156/5,05 | 132/4,883 | 128/4,852 | |
| + | + | – | + | 25/3,219 | 31/3,434 | 23/3,135 | 26,3/3,270 | |
| + | – | + | + | 135/4,905 | 129/4,86 | 85/4,443 | 116,3/4,756 | |
| + | + | + | + | 10/2,303 | 8/2,079 | 12/2,485 | 10/2,303 | |
| + | 124/4,82 | 68/4,22 | 45/3,807 | 79/4,369 |
Рассчитываем коэффициенты уравнения регрессии


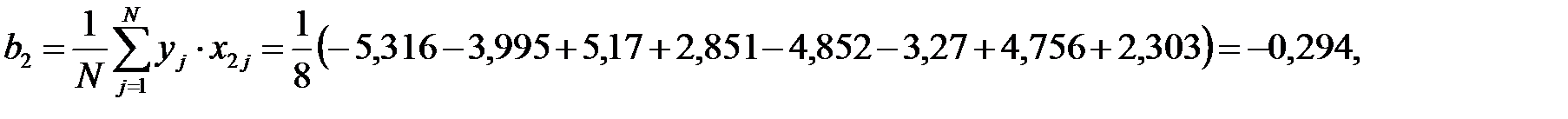

Тогда  .
.
Далее выполняется статистический анализ результатов математического моделирования, т.е. проверяется значимость коэффициентов уравнения регрессии, адекватность математической модели и т.п.
Вычисляем дисперсию для каждой строчки матрицы планирования по результатам 3-х параллельных (дублирующих) опытов по формуле

 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
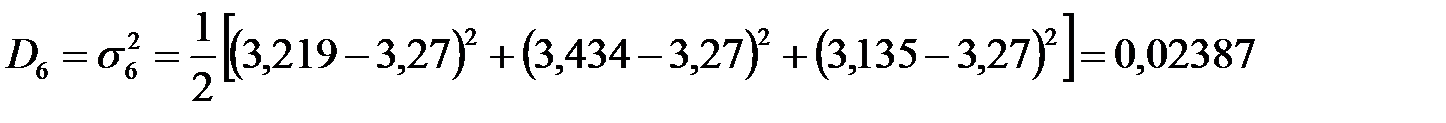 ,
,
 ,
,
 ,
,
 .
.
Проверяем результаты опытов на наличие грубых ошибок по критерию Груббса и устанавливаем, что резко выделяющиеся результаты отсутствуют.
Проверяем результаты опытов на однородность дисперсий по критерию Кохрена
 .
.
Табличное значение критерия Кохрена GT для доверительной вероятности PD = 0,95, N = 8 и  , GT = 0,516, т.е. Gp < GT и дисперсии считаются однородными.
, GT = 0,516, т.е. Gp < GT и дисперсии считаются однородными.
Определяем дисперсию воспроизводимости эксперимента
 .
.
Дисперсия ошибки определения i -го коэффициента уравнения регрессии (bi) будет
 ;
;  .
.
Доверительный интервал
 .
.
Для PD = 0,95 и числа степеней свободы  ,
,  . Тогда
. Тогда  . Так как
. Так как  , то все коэффициенты bi уравнения регрессии значимы.
, то все коэффициенты bi уравнения регрессии значимы.
Проверяем гипотезу адекватности, рассчитав критерий Фишера по формуле
 ,
,
где  .
.
Найдем значение  для каждой строки матрицы планирования экспериментов, вычислив предварительно значение
для каждой строки матрицы планирования экспериментов, вычислив предварительно значение  по математической модели.
по математической модели.
1)  ,
,
2)  ,
,
3)  ,
,
4)  ,
,
5)  ,
,
6)  ,
,
7) 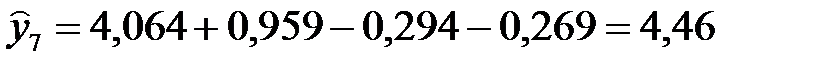 ,
,
8)  .
.
1)  ,
,
2)  ,
,
3)  ,
,
4)  ,
,
5)  ,
,
6)  ,
,
7)  ,
,
8)  ,
,
 ,
,
 ,
,
 .
.
При степени свободы числителя  и знаменателя
и знаменателя  с достоверностью PD = 0,95 табличное значение критерия Фишера FT = 3,01, т.е. FT > Fp и значит модель адекватна.
с достоверностью PD = 0,95 табличное значение критерия Фишера FT = 3,01, т.е. FT > Fp и значит модель адекватна.
Для перехода к математической модели в натуральных значениях факторов  в полученное уравнение регрессии вместо xi подставим их значения согласно формулам кодирования
в полученное уравнение регрессии вместо xi подставим их значения согласно формулам кодирования
 ;
;
 ;
;
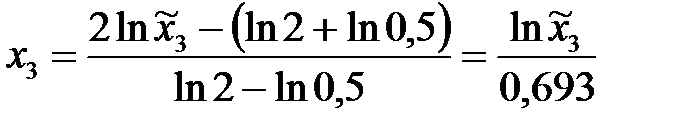 ;
;
 ;
;
 .
.
Потенцируя полученное уравнение, имеем окончательно
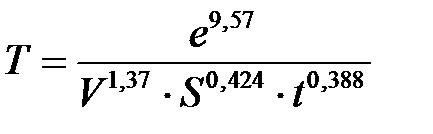 .
.
Расчеты стойкости по разработанной матмодели для условий экспериментов, представленных в матрице планирования, показали следующие результаты
Т 1 = 270,4 мин; Т 2 = 40 мин; Т 3 = 150,5 мин; Т 4 = 23,3 мин;
Т 5 = 157,8 мин; Т 6 = 23,3 мин; Т 7 = 87,8 мин; Т 8 = 13 мин; Т 9 = 36,3 мин
Сравнение экспериментальных данных с расчетными показывает, что они отличаются как в сторону увеличения, так и уменьшения стойкости. Максимальная разница между расчетным и экспериментальным значением стойкости имеет место в контрольном опыте №9 (54,3%). Такая большая разница указывает на большую нестабильность пластинок твердого сплава Т14К8, что также видно по выходному параметру, приведенному в матрице планирования экспериментов.
Поиск оптимума
Основной целью экстремальных экспериментов является нахождение наилучших (оптимальных) решений по выбранному критерию (параметру оптимизации). Для этого задается некоторый критерий оптимизации в виде целевой функции y, зависящий от управляемых параметров (факторов варьирования)
 .
.
Задача оптимизации сводится к отыскиванию таких значений параметров  , при которых целевая функция достигает экстремума (максимума или минимума). Будем считать оптимальным максимальное значение параметра оптимизации. Зависимость
, при которых целевая функция достигает экстремума (максимума или минимума). Будем считать оптимальным максимальное значение параметра оптимизации. Зависимость  образует некоторую поверхность в (k +1) мерном пространстве
образует некоторую поверхность в (k +1) мерном пространстве  , которую называют поверхностью отклика, а значение y в точках факторного пространства – откликом.
, которую называют поверхностью отклика, а значение y в точках факторного пространства – откликом.
Если бы поверхность отклика можно было описать в аналитической форме в виде приведенной функции, то координаты точки экстремума  можно найти, решив систему дифференциальных уравнений вида
можно найти, решив систему дифференциальных уравнений вида
 , где i = 1,2,…, k.
, где i = 1,2,…, k.
Решением системы является экстремальная точка (или «стационарная точка»), в которой градиент функции у обращается в нуль
 ,
,
где  – направляющий вектор координатной оси xi.
– направляющий вектор координатной оси xi.
Однако в большинстве случаев экспериментальных исследований аналитическая функция «у» неизвестна. Исследователь имеет возможность только экспериментально получить значение отклика при некоторой комбинации варьируемых факторов  . Полученное экспериментально значение отклика yэ всегда содержит случайную ошибку, т.е. оно будет отличаться от истинного значения yi на величину случайной ошибки опыта
. Полученное экспериментально значение отклика yэ всегда содержит случайную ошибку, т.е. оно будет отличаться от истинного значения yi на величину случайной ошибки опыта 
 .
.
Таким образом, задача оптимизации может быть решена двумя методами.
1) Каким-либо способом строиться математическая модель и задача решается аналитически или численным способом.
2) Поиск экстремальной («стационарной») точки в факторном пространстве 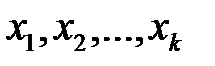 проводится экспериментально. При этом осуществляется локальное изучение поверхности отклика по результатам ряда экспериментов, специально спланированных вблизи выбранной точки. Экспериментальное значение отклика находится путем многократной исследовательской процедуры изучения поверхности отклика и продвижения в факторном пространстве. Для движения к оптимуму широко используется шаговый принцип, при котором строится математическая модель поверхности отклика и движение по факторному пространству осуществляется шагами с периодической оценкой правильности направления движения. Предполагается, что поверхность отклика гладкая, непрерывная и на ней имеется единственный оптимум. В этом случае, проводя ряд экспериментов, можно установить направление дальнейшего движения к оптимуму.
проводится экспериментально. При этом осуществляется локальное изучение поверхности отклика по результатам ряда экспериментов, специально спланированных вблизи выбранной точки. Экспериментальное значение отклика находится путем многократной исследовательской процедуры изучения поверхности отклика и продвижения в факторном пространстве. Для движения к оптимуму широко используется шаговый принцип, при котором строится математическая модель поверхности отклика и движение по факторному пространству осуществляется шагами с периодической оценкой правильности направления движения. Предполагается, что поверхность отклика гладкая, непрерывная и на ней имеется единственный оптимум. В этом случае, проводя ряд экспериментов, можно установить направление дальнейшего движения к оптимуму.
Известны несколько методов экспериментального поиска оптимума, различающихся способом определения направления движения и организацией самого движения. Рассмотрим наиболее широко применяемые экспериментальные методы.
Метод Гаусса-Зайделя
Этот метод базируется на принципе покоординатного восхождения, когда факторы изменяются поочередно и последовательно ищут локальные оптимумы на каждой из координат. Переход к новой (i +1) координате совершаются по достижении частного экстремума целевой функции у на предыдущем направлении, например, в точке Хh, в которой
 .
.
Найдя частные экстремумы по всем координатам  , снова переходят к варьированию первой (x 1), второй (x 2) и т.д. до (xk) координат.
, снова переходят к варьированию первой (x 1), второй (x 2) и т.д. до (xk) координат.
Характерной особенностью процесса является продолжительная стабилизация всех факторов, кроме одного, по которому происходит движение, на определенном уровне, т.е. фактически реализуется однофакторный эксперимент.
Направление движения вдоль (i +1)-й координатной оси выбирается по результатам двух пробных экспериментов  и
и 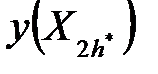 в окрестностях базовой точки частного экстремума
в окрестностях базовой точки частного экстремума  по предыдущей i-й переменной.
по предыдущей i-й переменной.
Рассмотрим процедуру (алгоритм) поиска оптимума методом Гаусса-Зайделя на примере 2-х факторного процесса (рис.19).
| Xk |
| x 2,1 |
| x 1,1 |

|
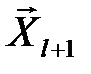
|

|

|

|
| X 2 |
| X 1 |

Рис.19. Метод Гаусса-Зайделя для 2-х факторного процесса
1) Определяются координаты начальной точки X 1 движения к оптимуму (на основании априорной информации).
2) Задается шаг варьирования  по каждой независимой переменной (фактору)
по каждой независимой переменной (фактору) 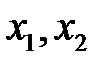 .
.
3) Для установления направления движения в первом цикле (вдоль оси X 1) выполняются пробные эксперименты, пробное движение с центром в начальной точке X 1(h *=1) вариацией параметра X 1 на  и
и  , т.е. выполняется два пробных шага в точке
, т.е. выполняется два пробных шага в точке
 ;
;
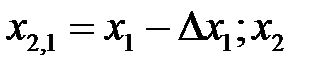 .
.
Производится измерение откликов  и
и  в этих точках.
в этих точках.
4) Отклики в пробных точках сравниваются и устанавливается характер изменения отклика.
5) Реализуется 1-й цикл рабочего движения с шагом  в направлении
в направлении
возрастания отклика  , т.к. ищется область максимума. Координаты последовательных точек этого движения будут
, т.к. ищется область максимума. Координаты последовательных точек этого движения будут
 ,
,
где  .
.
6) После каждого рабочего шага (эксперимента) проводится измерение значения отклика

7) 1-й цикл шагового движения прекращается по достижении в некоторой точке  частного экстремума целевой функции по соответствующей переменной.
частного экстремума целевой функции по соответствующей переменной.
 .
.
Критерием останова служит выполнение неравенства
 .
.
8) Точка  принимается за исходную для следующего цикла рабочего движения (по оси
принимается за исходную для следующего цикла рабочего движения (по оси  ) и базовой для новых пробных экспериментов в точках
) и базовой для новых пробных экспериментов в точках 
 ;
;
 .
.
Если в пробном движении по i -й переменной оба шага окажутся неудачными, т.е.  ; то переходят к варьированию следующим (i +1) параметром.
; то переходят к варьированию следующим (i +1) параметром.
9) Дальнейшая процедура выбора направления и организация II-го, III-го (вновь по оси  ) и дальнейших циклов движения аналогична описанному выше. Точка x в факторном пространстве занимает при этом последовательно следующие положения (координаты)
) и дальнейших циклов движения аналогична описанному выше. Точка x в факторном пространстве занимает при этом последовательно следующие положения (координаты)
 ,
,
 ,
,
…………………….
 ,
,
или
 .
.
10) После 2-го цикла рабочего движения переходят к третьему (вновь по  ) и т.д. Поиск прекращается в точке
) и т.д. Поиск прекращается в точке  , любое движение из которой приводит к уменьшению значения выходного параметра. Это будет точка экстремума целевой функции с точностью до максимального шага варьирования
, любое движение из которой приводит к уменьшению значения выходного параметра. Это будет точка экстремума целевой функции с точностью до максимального шага варьирования  .
.
Метод градиента
При оптимизации процесса градиентным методом рабочее движение совершается в направлении наиболее быстрого возрастания или убывания выходного параметра, т.е. в направлении максимального (по абсолютной величине) градиента целевой функции  . Направление движения корректируется после каждого рабочего шага (рис.20), т.е. каждый раз заново вычисляется значение вектора-градиента
. Направление движения корректируется после каждого рабочего шага (рис.20), т.е. каждый раз заново вычисляется значение вектора-градиента 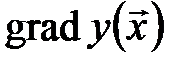 по результатам специально спланированных пробных экспериментов. Координатами вектора-градиента
по результатам специально спланированных пробных экспериментов. Координатами вектора-градиента  служат коэффициенты линейных членов разложения функции
служат коэффициенты линейных членов разложения функции  в ряд Тейлора по степеням
в ряд Тейлора по степеням  . Соответствующие компоненты вектора-градиента могут быть получены, как коэффициенты
. Соответствующие компоненты вектора-градиента могут быть получены, как коэффициенты  линейной аппроксимации поверхности отклика вблизи исходной точки
линейной аппроксимации поверхности отклика вблизи исходной точки 


|
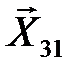
|
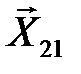
|
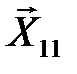
|
|
|
|


