Согласованный линейный фильтр

Лабораторная работа № 6

 

по дисциплине «Основы радиоэлектроники и связи»

 

 

Тема:

 

 

«Прохождение сигналов через согласованный фильтр»

 

 

Руководитель: проф. Трофимов А. Т.

Выполнил: студент гр. № 4141 Понкин Д. О.

 

 

Дубна, 2011

СОДЕРЖАНИЕ

ЦЕЛЬ РАБОТЫ.. 3

ЗАДАЧИ.. 3

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 4

2. ПРАКТИЧЕСКАЯ ЧАСТЬ. 8

2.1. Прохождение ЛЧМ сигнала через согласованный фильтр. 8

2.2. Прохождение гармонического сигнала через согласованный фильтр. 9

2.3. Прохождение прямоугольного импульса через согласованный фильтр. 10

ВЫВОДЫ.. 11

СПИСОК ЛИТЕРАТУРЫ.. 11

 

 

ЦЕЛЬ РАБОТЫ

Целью работы является закрепление знаний о согласованных фильтрах, используемых для обнаружения сигналов.

ЗАДАЧИ

В ходе выполнения лабораторной работы необходимо решить следующие задачи:

1. Получить модель прохождения ЛЧМ сигнала через согласованный фильтр.

2. Получить модель прохождения гармонического сигнала через согласованный фильтр.

3. Получить модель прохождения прямоугольного импульса через согласованный фильтр.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Прием радиосигналов всегда сопровождался помехами. Поэтому на протяжении всего развития радиотехники (в частности, приемных устройств) центральной проблемой была и остается борьба с помехами и шумами (далее просто шумами). В случаях, когда мощность полезного сигнала соизмерима со средней мощностью шума, трудно не только выделить, но и обнаружить сигнал.

Согласованный линейный фильтр

Основой большинства практических методов выделения сигнала из аддитивной смеси сигнала и шума в радиоприемных устройствах является оптимальная линейная фильтрация, использующая линейные частотные фильтры.

В теории приемных устройств установлено, что критерий качества линейной фильтрации зависит от одной из решаемых задач: обнаружение сигнала в шумах или разрешение сигналов. При обнаружении сигнала в шумах наиболее эффективен критерий максимума отношения сигнал/шум по мощности на выходе фильтра. Линейный фильтр, для которого это отношение максимально, называют оптимальным (подразумевая наилучшим). Следует ожидать, что при подаче на вход оптимального фильтра аддитивной суммы полезного сигнала и шума на его выходе можно получить заметное увеличение отношения сигнал/шум.

Одним из основных параметров фильтров приемника является коэффициент передачи. Коэффициент передачи оптимального фильтра приемника определим при условии, что сигнал принимается на фоне белого шума с двусторонней спектральной плотностью мощности W ₀ (хотя часто белый шум задается односторонней, т. е. в области физических частот спектральной плотностью мощности N ₀ = 2 W ₀).

Для удобства анализа представим коэффициент передачи оптимального фильтра в виде

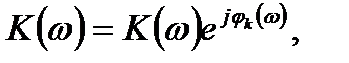(15.1)

где К (ω)— АЧХ; φ_k (ω) — ФЧХ фильтра.

Пусть входной сигнал u (t)имеет спектральную плотность

(15.2)

Здесь S (ω)и φ_c (ω) — соответственно амплитудный и фазовый спектры при­нимаемого сигнала.

Отметим некоторый, пока неизвестный, момент времени t = t ₀, при котором отношение сигнал/шум на выходе фильтра будет максимальным. Тогда сигнал на выходе фильтра (линейного четырехполюсника):

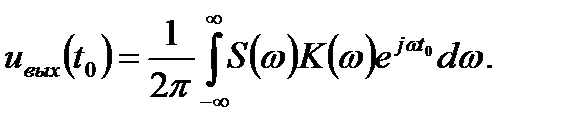(15.3)

Поскольку S _вых(ω) = S _вх(ω) K (ω), то средняя мощность (дисперсия) белого шума на выходе фильтра:

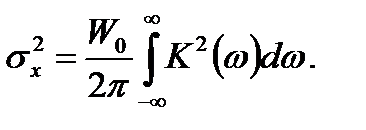(15.4)

Используя выражения (15.3) и (15.4), запишем отношение выходных мощностей сигнала и шума

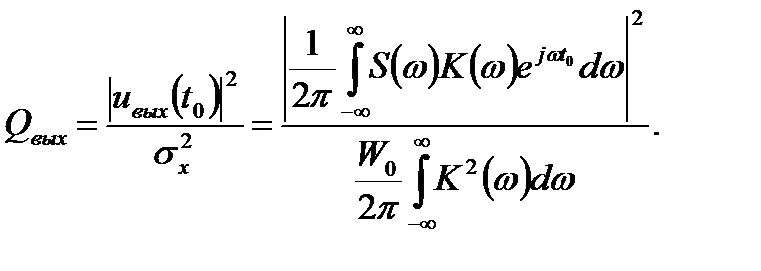(15.5)

Для удобства вычислений введем эквивалентный коэффициент передачи фильтра

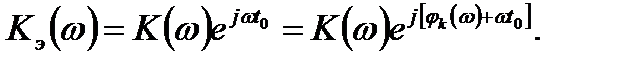(15.6)

Оптимальный коэффициент передачи анализируемого фильтра максимизирует правую часть выражения (15.5). Задача нахождения оптимального коэффициента передачи К (ω) решается на основе известного в математике неравенства Буняковского-Коши-Шварца, которое для данного случая имеет вид:

(15.7)

Прямая подстановка показывает, что неравенство обращается в равенство, если

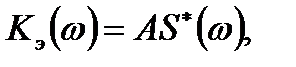(15.8)

где А — произвольный постоянный коэффициент; 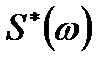— функция комплексно-сопряженная с S (ω).

Представим эквивалентный коэффициент передачи (15.8) в виде:

Отсюда находим коэффициент передачи фильтра

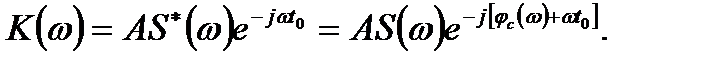(15.9)

Формула (15.9) полностью определяет коэффициент передачи оптимального фильтра, максимизирующего отношение сигнал/шум. Отсюда же следуют требования к АЧХ и ФЧХ оптимального фильтра:

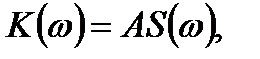(15.10)

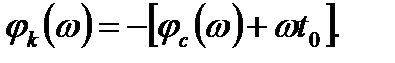(15.11)

По определению частотный коэффициент передачи — безразмерная величина, поэтому постоянный коэффициент А должен иметь размерность, обратную размерности амплитудного спектра входного сигнала S (ω).

Сущность метода обработки принимаемого сигнала оптимальным фильтром приемника иллюстрируется рисунке 1, где соответственно показаны и обозначены: спектры входных сигнала S (ω) и белого шума W ₀;спектр выходного сигнала S _вых(ω) и АЧХ фильтра K (ω); энергетический спектр выходного шума .

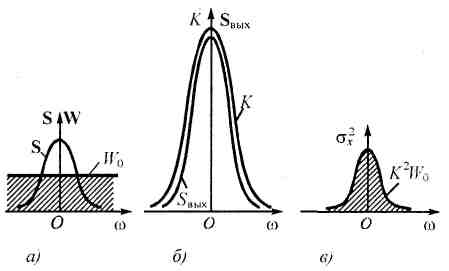
Рис. 1. Оптимальная фильтрация:

а — спектры входных сигнала и шума; б — спектр выходного сигнала и АЧХ фильтра; в — спектр выходного шума.

Эти результаты имеют глубокий физический смысл, формула (15.10) устанавлива­ет, что АЧХ фильтра K (ω)должна с точностью до масштабного множителя А совпа­дать по форме с амплитудным спектром S (ω) входного сигнала. Благодаря этому, подавляющая часть спектральных составляющих входного сигнала, имеющих наибольшие амплитуды, проходит на выход оптимального фильтра практически без ослабления и вносит основной вклад в образование его пикового значения. Из множества же спектральных компонентов входного белого шума, располагающихся в бесконечной полосе частот, на выход фильтра проходят и не ослабляются только те, которые находятся под кривой его АЧХ, т. е. в ограниченной полосе частот. Это приводит к ослаблению средней мощности шума на выходе фильтра по сравнению со спектральной плотностью мощности белого шума W ₀на входе. В результате этого отношение сигнал/шум на выходе оптимального фильтра увеличивается.

Соотношение (15.11), описывающее фазочастотную характеристику оптимального фильтра, можно трактовать как условие компенсации начальных фаз всех гармонических составляющих спектра сигнала. Согласно этому условию, оптимальный фильтр должен иметь такую ФЧХ, чтобы получаемый в нем фазовый сдвиг каждой гармоники – φ_с (ω) был равен по величине и противоположен по знаку начальной фазе соответствующей составляющей спектральной плотности S (ω) входного сигнала. Оптимальный фильтр проводит компенсацию («обнуление»)начальных фаз всех спектральных составляющих сигнала u (t), в результате чего образуется и пик выходного сигнала. Составляющая ФЧХ – ωt ₀ указывает на то, что пик (максимум) выходного сигнала задержан относительно начала действия входного сигнала на время t ₀. Связь между фазовой характеристикой φ_с (ω) входного сигнала, компенсирующей ее фазовой характеристикой - φ_с (ω) и ФЧХ фильтра поясняется рис. 2. Фазовая характеристика выходного сигнала, определяемая формулой:

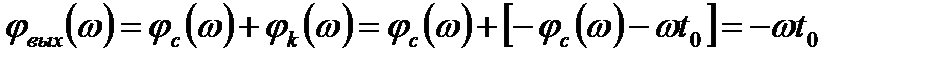. (15.12)

показана на этом рисунке прямой линией.

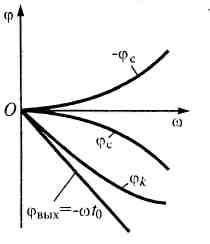
Рис. 2. Связь между фазочастотными характеристиками фильтра и сигнала.

Таким образом, коэффициент передачи фильтра, описываемый соотношением (15.1), согласован с амплитудным и фазовым (или фазовой характеристикой) спектрами входного сигнала. Поэтому анализируемый оптимальный фильтр часто называют согласованным.

Вернемся вновь к выражению (15.5) и рассмотрим энергетические соотношения между сигналом и шумом на выходе исследуемого оптимального фильтра. Поскольку квадрат модуля комплексного числа равен квадрату его действительной части, то, после несложных преобразований упомянутой формулы, получим:

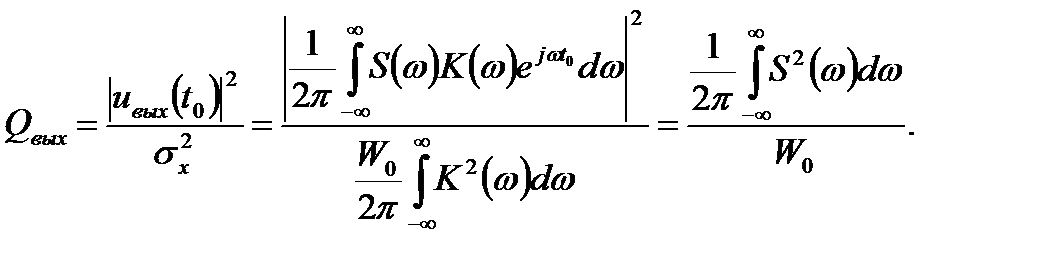(15.13)

Числитель в формуле (15.13) в соответствии с равенством Парсеваля представляет собой энергию входного сигнала Э. Тогда последнее соотношение примет вид:

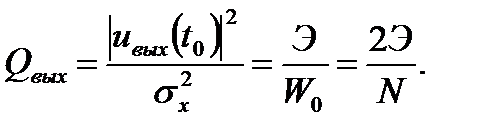(15.14)

 

ПРАКТИЧЕСКАЯ ЧАСТЬ

Поделиться:

Воспользуйтесь поиском по сайту: