Критерий Гурвица (оптимизма - пессимизма).

Игры с природой

Матричная игра, в которой игрок взаимодействует с окружающей средой, не заинтересованной в его проигрыше, и решает задачу определения наиболее выгодного варианта поведения с учетом неопределенности состояния окружающей среды называется статистической игрой или игрой с природой.

Игрок в этой игре называется лицом, принимающим решение.

В общем виде платежная матрица такой игры имеет вид:

	S1	S2	…	Sn
A1	а11	а12	...	а1n
A2	а21	а22	...	а2n
…	...	...	...	...
Am	am1	am2	...	amn

ЛПР определяет результат решения по критериям. Для того, чтобы прийти к однозначному и по возможности наиболее выгодному варианту решения, необходимо ввести оценочную функцию. При этом каждой стратегии ЛПР будет приписываться некоторый результат W_i, который характеризует все последствия этого решения. Из массива результатов принятия решения ЛПР выбирает элемент W_i, который наилучшим образом отражает мотивацию его поведения.

Для того чтобы можно сделать вывод о том какую именно стратегию выбирать игроку, необходимо использовать критерии Вальда, Гурвица, Сэвиджа, Лапласа, Байеса.

 

Критерий Вальда.

Рекомендуется применять максиминную стратегию, отражает принцип гарантированного результата.

Критерий олицетворяет позицию крайнего пессимизма: надо ориентироываться всегда на худшие условия, зная наверняка, что хуже этого уже не будет. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае, не меньший, чем нижняя цена игры с природой:

Правило выбора решения в соответствии с ММ-критерием:

1. матрица решений дополняется еще одним столбцом, каждый элемент которого представляет собой минимальное значение каждой стратегии ЛПР: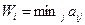

2. Оптимальной по данному критерию считается стратегия для которой минимальное значение выигрыша максимально:

Выбранные таким образом варианты полностью исключают риск. Это означает, что ЛПР не может столкнуться с результатом хуже, чем тот, на который он ориентируется. Поэтому ММ-критерий считается одним из фундаментальных, в технических задачах он применяется чаще всего. Однако нежелание рисковать приводит к различным потерям.

Применение ММ-критерия оправдано, если ситуация в которой принимается решение следующая:

1. о возможности появления внешних состояний окружающей среды ничего не известно;
2. приходится считаться с появлением различных внешних состояний окружающей среды;
3. решение реализуется один раз;
4. необходимо исключить какой бы то ни было риск.

 

Критерий максимума

Олицетворяет позицию крайнего оптемизма. Наиболее простой критерий, основывающийся на идее, что ЛПР, имея возможность в некоторой степени управлять ситуацией, рассчитывает, что произойдет такое развитие ситуации, которое для него является наиболее выгодным.

Правило выбора решения:

1. матрица решений дополняется еще одним столбцом, каждый элемент которого представляет собой максимальное значение каждой стратегии ЛПР:
2. Оптимальной по данному критерию считается стратегия для которой минимальное значение выигрыша максимально:

 

Критерий Гурвица (оптимизма - пессимизма).

Критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом (всегда рассчитывай на худшее), ни крайним легкомысленным оптимизмом (авось кривая выведет).

Стараясь занять наиболее уравновешенную позицию, ЛПР может ввести оценочный коэффициент, называемый коэффициентом пессимизма и отражает ситуацию промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. ().

При γ = 1 критерий превращается в критерий Вальда, при γ = 0 - в критерий максимума. На γ оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем γ ближе к единице.

Данный коэффициент определяется на основе статистических данных или на основе личного опыта ЛПР в схожих ситуациях. При отсутствии ярко выраженной склонности к оптимизму или пессимизму выбор γ = 0,5 представляется наиболее разумным.

Правило выбора решения:

1. 
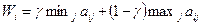
2. Оптимальной по данному критерию считается стратегия для которой минимальное значение выигрыша максимально:

Применение критерия оправдано, если:

1. Информация о состояниях окружающей среды отсутствует или недостоверна;
2. приходится считаться с появлением различных внешних состояний окружающей среды;
3. решение реализуется малое количество решений;
4. допускается некоторый риск.

 

Критерий Сэвиджа.

Это критерий относительного пессимизма, который оперирует понятием риска, или остатка.

Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

Для составления матрицы рисков каждый элемент матрицы решений вычитается из наибольшего результата соответствующего столбца:

Правило выбора решения:

1. матрица рисков дополняется столбцом наибольших значений коэффициентов
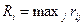
2. Оптимальной по данному критерию считается стратегия для которой минимальное значение выигрыша максимально:

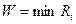
Требования, предъявляемые к ситуации, в которой принимается решение, совпадают с требованием к ММ-критерию, но наиболее существенным является учет степени воздействия фактора риска на величину выигрыша.

 

Критерий Лапласа.

Этот критерий основывается на принципе недостаточного обоснования. Поскольку вероятности состояния не известны, необходимая информация для вывода, что эти вероятности различны, отсутствует. Поэтому можно предположить, что они равны.

Правило выбора решения:

1. матрица решений дополняется столбцом, в котором определяется среднее значение выигрыша:
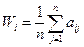
2. Оптимальной по данному критерию считается стратегия для которой:

Применение критерия оправдано, если:

1. ЛПР не имеет информации, либо имеет неполную информацию о вероятностях состояний окружающей среды;
2. вероятности состояний окружающей среды близки по своему значению
3. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.

 

Поделиться:

Воспользуйтесь поиском по сайту: