Спецификации числовых данных

Lesson 3

Приближенные вычисления

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы. Под численными методами подразумеваются методы решения задач, сводящиеся к действиям над числами, то есть к тем действиям, которые выполняет компьютер.

Решение, полученное численным методом, обычно является приближенным, то есть содержит некоторую погрешность. Это происходит потому, что численным методом обычно решается другая, более простая задача, приближающая исходную задачу. В ряде случаев численный метод строится на базе бесконечного процесса, который, прерванный на некотором шаге, дает приближенное решение.

Большинство численных методов основано на замене сложных объектов более простыми. Одно из главных понятий в математике – функция. Наиболее удобной для расчетов функцией является многочлен. Его значения просто вычисляются, поэтому алгебраические многочлены широко применяются для приближения функций.

Ряд Тейлора

Большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания.

Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Ряды Тейлора применяются для аппроксимации функции многочленами.Аппроксимация (приближение) – это научный метод, состоящий в замене одних формул другими, более простыми для расчета.

Запись бесконечного ряда Тейлора:

a_n называется общим членом ряда.

Сумму бесконечного ряда невозможно считать так же, как конечную сумму. Поэтому следует ввести несколько определений.

Частичной суммой ряда называется выражение вида

Можно составить бесконечную последовательность частичных сумм S₀, S₁,… S_n,…:

S₀ = a₀

S₁ = S₀ + a₁

S₂ = S₁ + a₂ и так далее

Сходящимся называется ряд 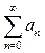, у которого последовательность частичных сумм имеет предел – число . Это число называется суммой сходящегося ряда. Если же последовательность частичных сумм стремится к бесконечности, ряд называется расходящимся.

Множество значений аргумента, при которых ряд сходится, называется областью сходимости этого ряда.

Необходимый признак сходимости ряда. Если ряд сходится, то предел общего члена ряда при бесконечном увеличении номера n равен нулю: .

Иллюстрацией к сказанному служат графики, построенные с помощью пакета AGrapher:

График зависимости членов ряда и частичных сумм от номера члена ряда для разложения функции sin(4.0)

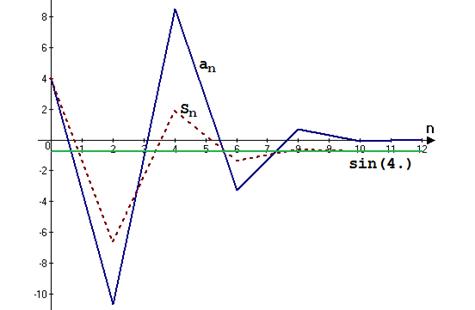
График зависимости членов ряда и частичных сумм от номера члена ряда для разложения функции CosH(3.0) (гиперболический косинус)

Точность вычислений

Чтобы получить приближенное значение функции, вычисляя сумму ряда, следует ограничить количество слагаемых. При замене бесконечной суммы частичной суммой ряда вносится методическая погрешность, которая количественно оценивается по первым отброшенным членам ряда.

Выбирая критерий (условие) прекращения суммирования ряда, воспользуемся необходимым признаком сходимости ряда . Это означает, что для любого положительного ε существует номер n, начиная с которого для всех членов ряда |a_n| < ε. Выбрав значение ε достаточно малым, можно прекратить суммирование ряда при условии
| a_n | < ε.

Значение ε будем называть заданной погрешностью вычислений. Точность вычислений тем выше, чем меньше погрешность. Очевидно, что заданная погрешность не может быть равна 0.

Выбирая точность вычислений, надо исходить из целей решаемой задачи. Например, для изображения графика на экране компьютера вполне достаточно погрешности
ε =10^-2.

Для переменных типа real достижима минимальная погрешность ε =10^-6 ÷ 10^-7; используя переменные типа double precision, можно выбрать погрешность
ε =10^-15 ÷ 10^-16.

Если задать слишком высокую степень точности, не согласовав ее с типами используемых переменных, например, ε =10^-15 для переменных типа real, программа может зациклиться, так как неравенство | a_n | < ε никогда не выполнится.

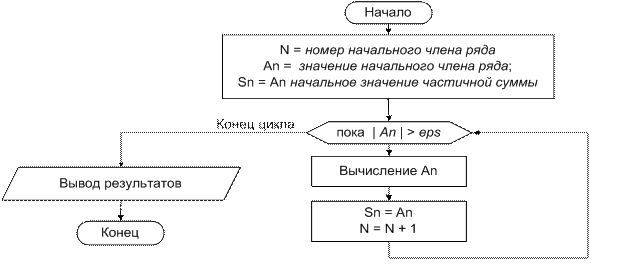
Общая идея решения поставленной задачи иллюстрируется блок-схемой.

1) Переменная An используется в программе для вычисления текущего члена ряда из последовательности a₀ , a₁ , … a_n, по очереди принимая перечисленные значения. Аналогично переменная Sn по очереди принимает значения частичных сумм. После выхода из цикла переменная Sn равна сумме ряда.

2) Суммирование членов ряда выполняется в цикле
do while «пока | An| > eps», выход из цикла при условии | a_n | < ε.

Кроме методической погрешности на общую погрешность вычислений, влияет постоянно накапливающаяся погрешность округления. Погрешность округления – это инструментальная погрешность, связанная с ошибками процессора при работе с вещественными числами. Уменьшение погрешности округления достигается применением рекуррентных формул.

Рекуррентная формула

При суммировании ряда необходимо решить следующие задачи:

a) свести вычисления к простейшим арифметическим операциям;

b) уменьшить число этих операций и время расчета;

c) уменьшить погрешность округления.

Рассмотрим вычисление функции sin x. Разложение этой функции в ряд Тейлора имеет следующий вид

.

Область сходимости ряда определяется неравенством , то есть ряд сходится при любом значении x.

Величина n! называется “ n - факториал” и вычисляется по формуле:

n! = 1 × 2 × 3 × … × (n – 1) × n = (n – 1)! × n или

Принято считать, что 0! = 1.

Суммирование ряда последовательным вычислением слагаемых и добавлением их к сумме, как на приведенной выше блок-схеме, сводит вычисления к простейшим арифметическим операциям, то есть первая задача при этом решается. Что касается второй задачи – уменьшения количества этих операций, – то многократное перемножение чисел в числителе (степени x) и в знаменателе (n!) вряд ли можно считать рациональным. При этом (третья задача) погрешность вычислений возрастает с увеличением номера члена ряда – слишком велики становятся и числитель, и знаменатель.

Задачи сокращения количества операций и уменьшения погрешности вычислений решает рекуррентная формула, позволяющая вычислить значение очередного члена ряда, используя уже найденное значение предыдущего. Рекуррентная формула имеет вид:

a_n+1 = a_n × T_n, где T_n – коэффициент рекурсии.

В нашем примере произвольный член ряда определяется формулой:

, где n = 0, 1, 2,...

Номер начального члена ряда n = 0, его значение a₀ = x.

Для расчета коэффициента рекурсии

определим значение следующего (n+1)-го члена ряда.

В формулу общего члена ряда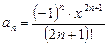

вместо n подставим (n+1), получим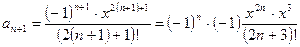

Вычисляя коэффициент рекурсии, сокращаем дробь:

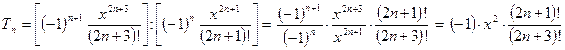
Чтобы сократить факториалы, рассмотрим числитель и знаменатель отдельно:

(2 n + 1)! = 1 × 2 × 3 × … × (2 n + 1)

(2 n + 3)! = 1 × 2 × 3 × … × (2 n + 1) × (2 n + 2) × (2 n + 3)

Окончательная формула коэффициента рекурсии

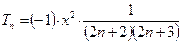
Отсюда получаем рекуррентную формулу для вычисления членов ряда

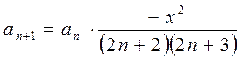
Проверка полученной формулы убережет Вас от ошибок в алгоритме и, возможно, сэкономит усилия при отладке программы.

Подставив n = 0 в формулу общего члена ряда , получаем a₀ = x.

Далее определим по рекуррентной формуле a₁ и a₂, сверяя результаты с соответствующими членами ряда:

при n = 0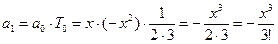

при n = 1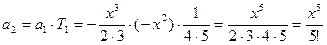

Совпадение полученных значений с членами ряда показывает, что коэффициент рекурсии рассчитан правильно.

Блок-схема алгоритма

В приведенную выше блок-схему подставим данные для расчета функции sin x, добавив вывод данных для графиков и защиту от зацикливания. Расчет текущего члена ряда на каждой итерации цикла осуществляется по полученной рекуррентной формуле.

Пояснения.

1) В переменной F хранится эталонное значение функции, вычисленное по стандартной программе, для последующего сравнения этого значения с полученной суммой ряда (|F–Sn|).

2) В процессе суммирования ряда формируются файлы с расширением .txt, содержащие таблицы зависимости значений членов ряда и частичных сумм от номера члена ряда (Блок вывода *). Таблицы состоят из строк, в которых через пробел записаны значения функции и аргумента.

! Открыть три файла

open (1, file=‘An.txt’); open (1, file=‘Sn.txt’)

open (1, file=‘F.txt’)

! Вывод данных для графика

write (1, *) N, An; write (2, *) N, Sn

write (3, *) N, F

Эталонное значение функции F не зависит от номера члена ряда N, на графике ему соответствует линия, параллельная горизонтальной оси.

Для построения графика воспользуйтесь пакетом AGrapher.

3) Для предотвращения зацикливания программы из-за возможных ошибок, количество членов ряда N ограничено значением Nmax (например, 100). При N > Nmax суммирование прекращается и выдается аварийное сообщение с дополнительной информацией.

4) Для вывода результатов суммирования и аварийного сообщения в отладке удобно использовать оператор namelist.

5) В цикле do while переменная N служит для хранения номера последнего члена ряда, вошедшего в сумму. Поскольку в нашем примере члены ряда в разложении функции нумеруются с 0, то количество просуммированных членов ряда равно N+1. Единица добавляется к N после выхода из цикла (Блок **).

Текст программы

Отладка программы

Если программа завершилась аварийно, или если полученные результаты не соответствуют ожидаемым результатам, рекомендуется провести анализ возможных причин этого.

Если вследствие ошибок в программе исследуемый ряд стал расходящимся, то программа обязательно закончится аварийно. Но это не значит, что аварийно завершается только суммирование расходящихся рядов.

Предположим, что выбранное значение Nmax=100, а для достижения заданной точности при выбранном аргументе требуется сумма из 120 слагаемых. Ряд сходится, но программа при этом завершится аварийно.

При аварийном завершении программы обычно рекомендуется выводить информацию, позволяющую анализировать создавшуюся ситуацию. Так и в нашей программе выводятся значения x, An, F, Sn, N, Nmax. Отличить расходящийся ряд от сходящегося можно, анализируя значение последнего просуммированного члена ряда An. Если значение его модуля приближается к значению заданной погрешности, то, возможно, ряд просто «не успел» сойтись, поэтому рекомендуется увеличить значение Nmax и повторить вычисления.

Если же значение | An | на порядки превышает значение погрешности, то бесполезно изменять Nmax, потому что ряд расходится. К этому могут привести следующие ошибки:

- Значение аргумента x не принадлежит области сходимости ряда.

- Заданная погрешность вычислений ε не согласована с типом используемых переменных; например, используя переменные типа real нельзя получить результат с точностью до 17-го десятичного знака (минимальная допустимая погрешность ε =10^-6 ÷ 10^-7).

- Допущены ошибки в рекуррентной формуле, алгоритме или программе.

Альтернативная блок-схема

У каждой задачи в программировании обычно имеется не одно решение. Покажем, как можно решить задачу суммирования ряда на примере разложения функции sin x. В этом алгоритме используется цикл по целой переменной N – номеру члена ряда. Все, сказанное об алгоритме, приведенном выше, относится и к этому варианту.

Bвод и вывод данных

При вводе или выводе данных происходит преобразование данных из текстового представления во внутреннее и обратно. Чаще всего, это обмен данными между программой и внешним носителем информации, обычно файлом или экраном компьютера.

Для ввода и вывода данных в Фортране служат операторы read и write.

Общая форма этих операторов имеет вид:

read (управляющая информация) список переменных

write (управляющая информация) список констант, переменных и выражений

Обмен данными происходит в порядке следования элементов списка.

В список управляющей информации входят:

1) На первом месте в списке – параметр, задающий номер устройства, который имеет вид:
n или символ «*»
где n – целая константа без знака, условный номер, связанный с устройством ввода-вывода (в частном случае с файлом), а символ «*» указывает, что номер устройства задан по умолчанию – клавиатура для ввода и экран для вывода.

2) На втором месте – параметр, определяющий формат ввода или вывода, который имеет вид:
n или ‘(символьное выражение)’ или «*»
где n – метка оператора format, соответствующая оператору ввода или вывода, символьное выражение – спецификация формата, а символ «*» указывает, что формат выбирается компилятором по умолчанию, при этом ввод и вывод производится под управлением списка.

Операторы open и close

Оператор open связывает условный номер устройства с файлом для ввода или вывода данных (“открывает” файл):

open( номер устройства, file= имя файла )

На номер устройства ссылаются операторы read и write. Можно открыть несколько файлов, но каждому из них должен быть сопоставлен уникальный номер устройства. Имя файла – символьная строка.

Если файл не существует, он создается, а если такой файл существует, то он обновляется при выводе. Другие возможности работы с файлами регулируются дополнительными параметрами.

Оператор close отсоединяет файлы от устройства (“закрывает” файлы):
close (список номеров устройств)

Не обязательно явно закрывать открытые файлы. При нормальном завершении программы каждый файл, открытый в ней, закрывается. Однако, следует закрыть файл, если необходимо открыть другой файл на этом же устройстве, не выходя из программы.

Пример.

open (1, file= ’in.txt’)

open (2, file= ’out.txt’)

read (1,*) a, b

write (2,*) "a =", a, " b =", b, " a+b =", a+b

close (1, 2)

Оператор read – ввод данных

При вводе данные, подготовленные в символьном виде, преобразуются в значения переменных списка в соответствии с форматом (форматный ввод) или с типами переменных (ввод под управлением списка).

Данные, подготовленные для ввода под управлением списка, разделяются между собой запятыми, пробелами или символами конца строки (клавиша <Enter>).

Данные для форматного ввода следует готовить строго в соответствии с выбранным форматом. Это не всегда удобно и используется редко.

Некоторые свойства оператора read:

1) Данные при вводе контролируются

Пример. Ввести число из файла 'data.txt':

1.23

Фрагмент для чтения:

integer m

open (7, file='data.txt')

read (7, *) m

Попытка ввести вещественное значение для целой переменной приведет к ошибке ввода, которая будет зафиксирована на экране монитора (ошибка выполнения): Run-time error F6101: READ(data.txt) – invalid INTEGER

2) В некоторых случаях данные конвертируются в соответствии с типом переменной. Например, если для ввода вещественных переменных подготовлены целые числа, в результате ввода переменным будут присвоены вещественные значения с нулевой дробной частью.

Пример. Ввести числа из файла 'data.txt':

123, 21, 17

Фрагмент для чтения:

real a, b, c

open (7, file='data.txt')

read (7, *) a, b, c! a= 123.0; b= 21.0; c= 17.0

3) Каждый оператор read начинает читать данные с новой строки, независимо от того, все ли данные предыдущей строки прочитаны.

Пример. Прочитать две строки из файла 'data.txt':

1.23, 4.56 77 55

11, 13

Фрагмент программы для чтения:

real x,y,z; integer m,n

open (7,file='data.txt')

read (7,*)x, y, z! x= 1.23; y= 4.56; z= 77.0

read (7,*)m, n! m= 11; n= 13

4) В списке управляющей информации оператора read может присутствовать необязательный параметр end вида
end = метка
Этот параметр указывает, что при достижении конца файла в случае отсутствия ошибок ввода, управление будет передано оператору с меткой метка. Использование этого параметра удобно, когда неизвестно, сколько данных подготовлено в файле.

Пример.

real x, y, z

do

read (*,*, end=99) x, y, z

write (*,*) x, y, z, sin(x) + sin(y) + sin(z)

Enddo

99 continue! продолжение программы

Цикл будет продолжаться до тех пор, пока не будут введены все числа, подготовленные в файле.

Примечание. Оператор continue – пустой оператор, по которому не производится действий, а выполнение программы продолжается со следующего оператора.

5) Чтобы избежать аварийного завершения программы вследствие ошибки ввода данных, можно запрограммировать переход на обработку ошибки ввода, указав метку в качестве значения дополнительного параметра err в операторе read, например:

Пример.

integer m,n

do

read (*,*, err=88) m, n

...

Exit

88 write (*,*) ‘ Re-enter the data’! Повторите ввод данных

Enddo

Цикл будет продолжаться до тех пор, пока не будут введены целые значения.

Оператор write – вывод данных

При выводе для данных, включенных в список, формируются строки символов в соответствии с форматом, выбранным программистом или назначенным компилятором по умолчанию.

Каждый оператор write начинает вывод данных с новой строки.

Вывод под управлением списка не всегда удобен по ряду причин. Далеко не всегда формат вывода, определенный компилятором, оптимален для оформления результатов. Вследствие своей простоты такой вывод удобен при отладке программ, но для создания привлекательного программного продукта лучше пользоваться форматным выводом.

Оператор format

Форматный вывод позволяет программисту самому определять расположение выводимых данных на устройстве вывода. Операторы format являются неисполняемыми операторами, но в отличие от других неисполняемых операторов, они могут находиться в любом месте программы.

Общая форма оператора format имеет вид:

метка format (список спецификаций)

Метка является обязательной частью оператора format. На нее ссылается хотя бы один оператор ввода или вывода в программе.

Список спецификаций (дескрипторов) состоит из ряда спецификаций (дескрипторов) формата, заключенных в скобки. Разделителями между ними служат запятые или символ «/» – признак перехода к новой строке при выводе.

Пример:

real radius = 1

open (2, file=’Out.txt’)

write (2,55) 2*3.14*radius

55 format ('длина окружности'/2x,'с=',F5.2)

Здесь оператор write, используя оператор format с меткой 55, выводит в файл Out.txt две строки (символ «_» означает пробел):

длина окружности

__c=_6.28

Спецификации, использованные в операторе format:

- 'длина окружности' и 'с=' – символьные константы, используемые как пояснительный текст;

- 2x – два пробела;

- F5.2 – формат для вывода вещественного числа; число занимает в строке вывода пять позиций, из которых две отводятся под дробную часть.

На один оператор format могут ссылаться несколько операторов вывода. Если список спецификаций используется однократно, то он может быть записан в виде символьного выражения в операторе write. Это выражение заключается в кавычки; кавычки в списке спецификаций должны отличаться от кавычек, обрамляющих выражение (простые и двойные или наоборот).

Пример:

write (2, "(1x,'c=',F5.2)") c

Внимание! Синтаксис символьного выражения в операторе вывода не контролируется компилятором, и ошибки в его написании будут выявлены только на этапе выполнения, в отличие от оператора format с меткой. Поэтому в операторе вывода write не рекомендуется писать длинные списки спецификаций.

Спецификации числовых данных

Спецификации числовых данных: rIw, rFw.d, rEw.d, rDw.d, rGw.d

Во всех спецификациях задается ширина поля вывода w – целое число без знака, задающее количество символьных позиций для вывода числа. Число «прижимается» к правому краю поля вывода и при необходимости дополняется слева пробелами. Если ширина поля вывода недостаточна для размещения числа, то выводятся символы «*», их количество равно ширине поля.

Для положительных чисел знак «+» обычно не выводится.

Целое число без знака r называется повторителем спецификации; оно указывает, сколько раз должна быть повторена спецификация. Если повторитель отсутствует, то по умолчанию спецификация повторяется один раз.

Необходимо строго согласовывать спецификации для выводимых данных с их типом. Например, попытка вывести значение вещественной переменной по I-спецификации для целых чисел приведет к ошибке вывода, которая будет зафиксирована на экране монитора (ошибка выполнения):
Run-time error F6102: WRITE(out.txt) – E, F, D or G edit descriptor expected for REAL
(Перевод: Ошибка выполнения в операторе WRITE(out.txt) – для вещественных значений ожидаются спецификации (дескрипторы) E, F, D или G)

I -спецификация формата.

Целые числа выводятся по I-спецификации формата. Общая форма этой спецификации имеет вид:

rIw

где r – повторитель, w – ширина поля вывода.

Пример. Вывод четырех чисел по формату I4

integer:: a= 7812, b=12, c=-32, d=-7812

12 format (I4, I4, I4, I4)

write (*, 12) a, b, c, d

Формат вывода чисел можно преобразовать, используя повторитель:

integer:: a= 7812, b=12, c=-32, d=-7812

12 format (4I4)

write (*, 12) a, b, c, d

В результате выполнения оператора write в обоих случаях выведется строка (символ «_» соответствует пробелу).

7812__12_-32****

Звездочки означают, что последнее число не поместилось в четыре позиции. Рассчитывая ширину поля вывода чисел, не забывайте о позиции для знака, если выводимое число может быть отрицательным. Кроме того, предпочтительно, чтобы выведенные числа разделялись между собой хотя бы одним пробелом, который можно включить в поле вывода.

Возможная форма записи I-спецификации

rIw.d

где r – повторитель, w –ширина поля вывода, а d определяет общее количество выводимых цифр числа (не только значащих). При необходимости каждое число дополняется слева нулями. В том же примере выведем числа, используя спецификацию I8.4:

integer:: a= 7812, b=12, c=-32, d=-7812

12 format (4I8.4)

write (*, 12) a, b, c, d

Результирующая строка:

____7812____0012___-0032___-7812

F -спецификация формата

Вещественные числа можно выводить с использованием F-спецификации формата. Общая форма этой спецификации имеет вид:

rFw.d

где r – повторитель, w определяет ширину поля вывода, а d задает количество цифр после десятичной точки. Выводимое значение при необходимости округляется по обычным правилам. Если число меньше единицы, то ноль перед десятичной точкой опускается, знак «+» у положительных чисел также не выводится.

Пример. Вывод пяти чисел по формату F6.2

real:: a=483.76, b=122.11, c=12.9, d=-0.076, e=-126.3

13 format (F6.2, F6.2, F6.2, F6.2, F6.2)

write (*, 13) a, b, c, d, e

Преобразуем формат, используя повторитель:

real:: a=483.76, b=122.11, c=12.9, d=-0.076, e=-126.3

13 format (5F6.2)

write (*, 13) a, b, c, d, e

Результирующая строка в обоих случаях («_» соответствует пробелу):

483.76122.11_12.90__-.08******

Первое и второе числа «склеились», так как ширина поля недостаточна и не позволяет отделить числа одно от другого.

Третье число дополнено справа нулем (должно быть два символа в дробной части).

Четвертое число округлено, ноль в целой части опущен.

Звездочки означают, что последнее число не поместилось в шесть позиций. В самом деле, из шести позиций поля вывода две отведены под дробную часть, одна – под десятичную точку, и для целой части вместе со знаком остается три позиции. Таким образом, по формату F6.2 можно вывести число, находящееся в интервале [-99; 999].

Поделиться:

Воспользуйтесь поиском по сайту: