 |
Метод Ньютона (метод касательных)
|
|
|
|
Lesson 6
Численные методы
На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы.
Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами. В зависимости от сложности задачи, заданной точности, применяемого метода может потребоваться огромное количество действий, и здесь без быстродействующего компьютера не обойтись.
Решение, полученное численным методом, обычно является приближенным, т. е. содержит некоторую погрешность. Источниками погрешности приближенного решения задачи являются:
- погрешность метода решения;
- погрешности округлений в действиях над числами.
Погрешность метода вызвана тем, что численным методом обычно решается другая, более простая задача, аппроксимирующая (приближающая) исходную задачу. В ряде случаев численный метод представляет собой бесконечный процесс, который в пределе приводит к искомому решению. Процесс, прерванный на некотором шаге, дает приближенное решение.
Погрешность округления зависит от количества арифметических действий, выполняемых в процессе решения задачи. Для решения одной и той же задачи могут применяться различные численные методы. Чувствительность к погрешностям округления существенно зависит от выбранного метода.
Решение нелинейных уравнений
Постановка задачи
Решение нелинейных уравнений с одним неизвестным является одной из важных математических задач, возникающих в различных разделах физики, химии, биологии и других областях науки и техники.
|
|
|
В общем случае нелинейное уравнение с одним неизвестным можно записать:
f (x) = 0,
где f (x) – некоторая непрерывная функция аргумента x.
Всякое число x0, при котором f (x0) ≡ 0, называется корнем уравнения f (x) = 0.
Методы решения нелинейных уравнений делятся на прямые (аналитические, точные) и итерационные. Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по этой формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.
Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для алгебраического уравнения выше четвертой степени не удается получить аналитического решения в виде формулы с конечным числом арифметических действий. Во всех таких случаях приходится обращаться к численным методам, позволяющим получить приближенные значения корней с любой заданной точностью.
При численном подходе задача о решении нелинейных уравнений разбивается на два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.
Локализация корней
Для отделения корней уравнения f (x) = 0 необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке [ a, b ] имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке.
Если функция f (x) непрерывна на отрезке [ a, b ], а на концах отрезка её значения имеют разные знаки, т. е.
f(a) × f(b) < 0,
то на этом отрезке расположен, по крайней мере, один корень.
|
|
|

Рис 1. Отделение корней. Функция f (x) не монотонна на отрезке [ a, b ].
Это условие, как видно из рисунка (1), не обеспечивает единственности корня. Достаточным дополнительным условием, обеспечивающем единственность корня на отрезке [ a, b ] является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием постоянства знака первой производной f ′(x).
Таким образом, если на отрезке [ a, b ] функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень.
Воспользовавшись этим критерием, можно отделить корни аналитическим способом, находя интервалы монотонности функции.
Отделение корней можно выполнить графически, если удается построить график функции y = f (x). Например, график функции на рисунке (1) показывает, что эта функция на интервале [a, b] может быть разбита на три интервала монотонности и на этом интервале у нее существуют три корня.
Отделение корней можно также выполнить табличным способом. Допустим, что все интересующие нас корни уравнения (2.1) находятся на отрезке [ A, B ]. Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи.

Рис. 2. Табличный способ локализации корней.
Будем вычислять значения f (x), начиная с точки x = A, двигаясь вправо с некоторым шагом h (рис. 2). Как только обнаруживается пара соседних значений f (x), имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.
Надежность табличного способа отделения корней уравнений зависит как от характера функции f (x), так и от выбранной величины шага h. Действительно, если при достаточно малом значении h (h <<| B − A |) на границах текущего отрезка [ x, x + h ] функция f (x) принимает значения одного знака, то естественно ожидать, что уравнение f (x) = 0 корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции f (x) на отрезке [ x, x + h ] могут оказаться корни уравнения (рис. 3а).

Рис 3а Рис 3б
Также несколько корней на отрезке [ x, x + h ] могут оказаться и при выполнении условия f(x) × f(x+h) < 0 (рис. 3б). Предвидя подобные ситуации, следует выбирать достаточно малые значения h.
|
|
|
Отделяя таким образом корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска (h /2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.
Уточнение корней
На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку [ a, b ], с заданной точностью (погрешностью) ε. Это означает, что вычисленное значение корня x~ должно отличаться от точного x0 не более чем на величину ε:
| x0 – x~| £ ε
Процедура численного определения приближенных значений корней нелинейных уравнений, как правило, состоит в выборе начального приближения к корню x0 Î[ a, b ] и вычислении по некоторой формуле последующих приближений, x1 x2 и т.д. Каждый такой шаг называется итерацией, а сами методы уточнения – итерационными методами. В результате итераций получается последовательность приближенных значений корня
x0, x1,..., xk,..., которая называется итерационной последовательностью. Если эти значения с ростом k стремятся к точному значению корня x0, то говорят, что итерационный процесс сходится:

Методы уточнения корней
Метод половинного деления
Считаем, что отделение корней уравнения f (x) = 0 проведено и на отрезке [ a, b ] расположен один корень, который необходимо уточнить с погрешностью ε. В качестве начального приближения корня принимаем середину этого отрезка: c0 = (a + b) / 2 (рис. 4):
|
|
|

Рис. 4. Метод половинного деления.
Затем исследуем значение функции f (x) на концах отрезков [ a, c0 ] и [ c0, b ]. Тот из отрезков, на концах которого f (x) принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового отрезка [ a1, b1 ] (на рис. 4 это отрезок [ a, c0 ]). Вторую половину отрезка [ a, b ], на которой f (x) не меняет знак, отбрасываем. В качестве следующего приближения корня принимаем середину нового отрезка
c1 = (a1 + b1) / 2 и т.д. Таким образом, k -е приближение вычисляется как
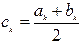
После каждой итерации отрезок, на котором расположен корень, уменьшается вдвое, а после k итераций в 2 k раз:
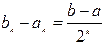
Прекратить итерационный процесс следует, когда будет достигнута заданная точность, т.е. при выполнении условия |x0 – ck| < ε
Поскольку корень x0 принадлежит отрезку [ ak, bk ], а ck – середина этого отрезка, то величина |x0 – ck| всегда будет меньше половины длины от резка [ ak, bk ] (см. рис. 4):

Следовательно, условие |x0 – ck| < ε будет выполнено, если
| bk – ak | < 2ε
Таким образом, итерационный процесс нужно продолжать до тех пор, пока не будет выполнено условие | bk – ak | < 2ε.
В отличие от большинства других методов уточнения, метод половинного деления сходится всегда, т.е. обладает безусловной сходимостью. Кроме этого он чрезвычайно прост, поскольку требует лишь вычисления значений функции f (x) и, поэтому применим для решения любых уравнений.
Однако метод половинного деления довольно медленный. С каждым шагом погрешность приближенного значения уменьшается в два раза, т.е.

поэтому данный метод является методом с линейной сходимостью.
З а м е ч а н и е. Метод половинного деления не требует знания дополнительной информации о функции на всем интервале [ a, b ]. Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных функций рассмотренный метод обладает гарантированной сходимостью. Если на этом интервале существует несколько корней уравнения, один из корней обязательно будет найден.
Метод хорд
Рассматриваемый метод так же, как и метод половинного деления, предназначен для уточнения корня на интервале [ a, b ], на концах которого функция f (x) принимает значения разных знаков. Очередное приближение в отличие от метода половинного деления берем не в середине отрезка, а в точке x, где пересекает ось абсцисс прямая линия (хорда), проведенная через точки А и В (рис. 5).

Рис. 5. Метод хорд.
Запишем уравнение прямой, проходящей через точки А и В:

Для точки пересечения прямой с осью абсцисс (x = x0, y = 0) получим уравнение
|
|
|

В качестве нового интервала для продолжения итерационного процесса выбираем тот из двух [ a, x0 ] и [ x0, b ], на концах которого функция f (x) принимает значения разных знаков. Для рассматриваемого случая (рис. 5) выбираем отрезок [ a, x0 ], так как
f(a) × f(x0) < 0. Следующая итерация состоит в определении нового приближения x1 как точки пересечения хорды AB1 с осью абсцисс и т.д.
Заканчиваем процесс уточнения корня, когда расстояние между очередными приближениями станет меньше заданной точности, т.е.
xk+1 – xk < ε
З а м е ч а н и е. Метод хорд и метод половинного деления очень похожи. При этом второй их них в ряде случаев дает более быструю сходимость итерационного процесса. Оба метода не требуют знания дополнительной информации о функции на всем интервале [ a, b ]. Например, не требуется, чтобы функция была дифференцируема. Даже для разрывных функций рассмотренные методы обладают гарантированной сходимостью.
Метод Ньютона (метод касательных)
Метод Ньютона также предназначен для уточнения корня на интервале [ a, b ], на концах которого функция f (x) принимает значения разных знаков. Но этот метод использует дополнительную информацию о функции f (x). Как результат он обладают более быстрой сходимостью, но в то же время, применим для более узкого класса функций, и его сходимость не всегда гарантирована.
Отделяя корни функции, следует учесть, что применение метода Ньютона требует, чтобы функция была монотонна и дважды дифференцируема, причем вторая производная f’’(x) на этом интервале не должна менять знак.
Cходимость итерационной последовательности, получаемой в методе Ньютона, зависит от выбора начального приближения x0. В общем случае, если задан интервал [ a, b ], содержащий корень, и известно, что функция f (x) монотонна на этом интервале, то в качестве начального приближения x0 можно выбрать ту границу отрезка [ a, b ], где совпадают знаки функции f (x) и второй производной f’’(x). Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.
Пусть нам известно начальное приближение к корню x0. Проведем в этой точке касательную к кривой y = f (x) (рис. 6). Эта касательная пересечет ось абсцисс в точке, которую будем рассматривать в качестве следующего приближения.

Рис. 6. Метод Ньютона
Значение x1 легко найти из рисунка:

выражая отсюда x1, получим

Аналогично могут быть найдены и следующие приближения. Формула для k+1 -го приближения имеет вид

Из этой формулы вытекает условие применимости метода: функция f (x) должна быть дифференцируемой и f ′ (x) в окрестности корня не должна менять знак.
Для окончания итерационного процесса могут быть использованы условия
f(xk) < ε или xk+1 – xk < ε
Численное интегрирование
Часто на практике не удается вычислить интеграл аналитическим путем. В этих случаях применяют приближенные методы численного интегрирования.
Постановка задачи
Часто на практике не удается вычислить интеграл аналитическим путем. В этих случаях применяют приближенные методы численного интегрирования.
Вычислить определенный интеграл
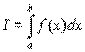
при условии, что границы интеграла а и b конечны и первообразная F (х) является непрерывной функцией х на всем интервале хÎ[a,b]. Во многих случаях, когда подынтегральная функция задана в аналитическом виде, интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница:

Однако этой формулой часто нельзя воспользоваться по следующим причинам:
- первообразная функция F(x) слишком сложна и ее нельзя выразить в элементарных функциях;
- функция f (x) задана в виде таблицы, что особенно часто встречается в задачах при обработке экспериментальных данных;
В этих случаях используются методы численного интегрирования. Задача численного интегрирования состоит в нахождении приближенного значения интеграла по заданным или вычисленным значениям.
Общий подход к решению задачи будет следующим. Определенный интеграл I представляет собой площадь, ограниченную кривой f (x), осью х и переменными х=а и х=b. Необходимо вычислить интеграл, разбивая интервал [ a,b ] на множество меньших интервалов, находя приблизительно площадь каждой полоски и суммируя их.
В зависимости от способа вычисления подынтегральной суммы существуют различные методы численного интегрирования (методы прямоугольников, трапеций, парабол, сплайнов и др.).
Метод прямоугольников
Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой:

Разобьём интервал интегрирования [ a, b ] на n равных частей. Обозначим D хi = h шаг разбиения. Формула прямоугольника применяется к каждому отрезку. В качестве точек xi выбираются левые(xi = хi – 1) или правые (xi = хi ) границы элементарных отрезков Соответственно, для этих двух случаев можно записать формулы метода прямоугольников:


Более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков: точка  . Таким образом, площадь криволинейной трапеции заменяется суммой прямоугольников с основанием h и высотами, равными значениям функции f (x) в середине оснований
. Таким образом, площадь криволинейной трапеции заменяется суммой прямоугольников с основанием h и высотами, равными значениям функции f (x) в середине оснований  . Получим формулу:
. Получим формулу:
 , где
, где  или
или 
Графическая интерпретация для левых, правых и центральных прямоугольников:



Метод трапеций
Метод трапеций использует линейную интерполяцию, т.е. график функции у = f (х) представляется в виде ломаной, соединяющей точки (хi, уi). В этом случае площадь всей криволинейной трапеции складывается из площадей элементарных прямоугольных трапеций

Площадь каждой трапеции определяется по формуле:
 ,
,  ,
,
где n - число интервалов разбиения., i=1,2,...,n.
Складывая площади элементарных трапеций, получим формулу трапеций для численного интегрирования:
 или
или 
Эти формулы можно представить в виде:
 или
или 
|
|
|


