Главная | Обратная связь | Поможем написать вашу работу!

Механизм долбежного станка.

Исходные данные:

Рис. 1 - Рычажный механизм перемещения долбяка

№ п/п	Параметр	Условное обозначение	Величина	Единицы измерения
	Размеры звеньев	l_OA	0,1	м
		l_OB	0,04	м
		l_BC	0,9	м
		l_CD	0,3	м
		=0.5 l_CD	0,15	м
	Параметры расположения звеньев	а	0,01	м
		b	0,02	м
		y₁	0,21	м
		y₂	0,39	м
	Частота вращения двигателя	n_дв		об/мин
	Частота вращения кривошипа 1	n₁		об/мин
	Масса звеньев рычажного механизма	m₃		кг
		m₄		кг
		m₅		кг
	Моменты инерции звеньев		0,20	кг м²
			0,18	кг м²
			0,04	кг м²
			0,10	кг м²
	Сила резания	Р_рез	1,9	кН
	Коэффициент неравномерности вращения кривошипа	δ	0,06	-
	Положение кривошипа при силовом расчете механизма	φ₁		град

I. Построение плана механизма для первого положения при φ=90⁰.

Для выполнения плана положения механизма примем масштабный коэффициент μ_l=l_CD/CD=0.005 м/мм, где l_CD=0.30 м - действительная длина звена CD; CD=60 мм - изображающий ее отрезок на чертеже.

Тогда чертежные размеры рычажного механизма будут равны:

ОА = l_OA/ μ_l=0.10/0.005=20мм;

ОВ = l_OB/μ_l=0.04/0.005=8 мм;

ВС = l_BC/ μ_l=0.09/0.005=18 мм;

CS₄= / μ_l=0.15/0.005=30 мм;

А = а/ μ_l=0.01/0.005=2 мм;

В = b/ μ_l=0.02/0.005=4 мм;

Y₁= y₁/ μ_l=0.21/0.005=42 мм;

Y₂= y₂/ μ_l=0.39/0.005=78 мм.

Сначала построим план 1 положения механизма, для определения положения опор 5 звена относительно точки D.

Для построения плана положения механизма:

1. Из точки О проводим отрезок ОА=20 мм под углом φ₁=240⁰, согласно схеме механизма.

2. На горизонтальной линии из точки О откладываем отрезок ОВ=8 мм, получим точку В.

3. Через точки А и В проводим линию, соответствующую отрезку АС.

4. Из точки В откладываем отрезок ВС=18 мм, получим точку С.

5. Из точки С до вертикальной линии, проходящей через точку В, откладываем отрезок CD=60мм.

6. Посередине отрезка CD откладываем точку S₄.

7. На расстояниях Y₁=60 мм, Y₂=100 мм, А=2 мм и В=4 мм достраиваем остальную часть рычажного механизма перемещения долбяка.

При построении плана механизма при φ=90⁰поступаем аналогичным образом, однако положения опор 5 звена относительно точки D берем из предыдущего построения.

II. Построение планов скоростей и ускорений

Для построения плана 2 положения механизма отрезок ОА откладываем под углом φ₁+30⁰=240+30=270⁰. Кривошип 1 вращается по часовой стрелке. Остальные построения выполняем аналогично, как для 1-го положения.

Для построения плана скоростей необходимо определить угловую скорость звена 1. Определим его по формуле

Кинематический анализ выполняется в последовательности определяемой формулой строения механизма I(0,1)→II(2,3)→III(4,5).

Скорость точки А разложим на две скорости, поскольку звено 2 взаимодействует как с первым звеном, так и с третьим.

Для механизма 1 класса:

скорость точки А₁, принадлежащей к 1 звену ;

примем масштабный коэффициент .

перпендикулярно ОА в направлении ω₁, тогда отрезок [ра₁] отложим перпендикулярно ОА в этом направлении.

Далее рассмотрим группу Ассура 2-3. Известными к началу рассмотрению являются и (поскольку принадлежит стойке). Первоначально определим скорость точки А₃.

Рассмотрим движение точки А₃ относительно точек А₁ и В₀, в векторном выражении запишем:

(параллельно отрезку АВ);

(перпендикулярно отрезку АВ).

Точку А₃ находим как пересечение решений этих 2-х уравнений.

Скорость точки С определим по теореме подобия:

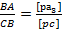; тогда [ . Размеры и ВА определяем из чертежа. Скорость точки С лежит по линии действия точки А₃.

Группа Ассура 4-5.

Известными к началу рассмотрению являются скорость точки C и (поскольку принадлежит стойке).

Скорость точки D рассмотрим относительно точек С и D₀, в векторном выражении запишем:

(перпендикулярно отрезку CD через С);

(параллельно у-у, вдоль направляющей).

Точка S₄ лежит посередине отрезка cd, поскольку =0.5 l_CD. Скорость точки S₄ определяем путем соединения полюса р с этой точкой.

Из плана скоростей находим линейные и угловые скорости:

;

Направление угловой скорости ω₃ звена 3 получим, поместив вектор относительной скорости в точку В и рассматривая поворот точки В относительно точки А₃. Аналогично определяется направление угловой скорости 4 звена.

Переходим к построению плана ускорений.

Ускорение точки А₁

;

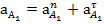где - нормальное ускорение точки А₁, направленное от точки А₁ к точке О.

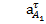- касательное (тангенциальное) ускорение точки А₁, направленное перпендикулярно ОА в сторону углового ускорения ε₁.

;

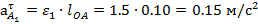Примем масштабный коэффициент ускорений 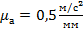и находим отрезки, изображающие и :

;

Из полюса плана ускорений π откладываем отрезок πn₁ в направлении . Поскольку 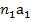равно нулю, то точки n₁ и а₁ совпадают. Значит данный отрезок будет полным ускорением точки А₁.

Далее на основании теоремы о сложении ускорений в плоском движении составляем векторные уравнения в порядке присоединения структурных групп.

Для определения ускорения точки А₃используем уравнения

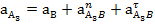
где - ускорение корриолиса, - релятивное ускорение кулисного механизма; (точка В неподвижна); 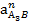и - нормальная и касательная составляющие ускорения точки А₃ при вращательном движении звена 2 относительно точки В. Вектор 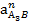направлен от точки В к точке А₃, - перпендикулярно АВ, вектор - параллельно АВ.

7,1 м/с².

Направление корриолисова ускорения получим, если повернуть вектор на 90⁰ в направлении

= 8.94 м/с².

Находим отрезки, изображающие эти ускорения

;

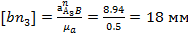Систему уравнений для ускорения 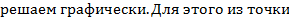а₁ откладываем отрезок в направлении через точку k проводим линию в направлении . Затем из точки b, совпадающей с полюсом π, откладываем отрезок [πn₃] в направлении 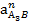и через точку n₃ - линию в направлении . В пересечении указанных линий получим точку а₃, которую соединяем с полюсом и получаем отрезок [πа₃], изображающий .

Точку с на плане ускорений находим по теореме подобия. Для этого вдоль отрезка πа₃ в противоположном направлении откладываем отрезок [πс], который находим из подобия

; .

Для определения ускорения точки D используем уравнения

;

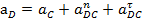где и - нормальная и касательная составляющие относительного ускорения точки D (по отношению к точке С), (так как точка D₀, принадлежащая стойке О и в данный момент совпадающая с точкой D, неподвижна), - относительное ускорение точки D по отношению к точке D₀ (направленное вдоль линии движения звена 5, то есть параллельно у).

м/с².

отрезок изображающий .

В соответствии с системой уравнений из точки с откладываем отрезок 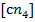в направлении , из точки n₄ проводим линию в направлении . Из точки d₀, расположенной в полюсе π, проводим линию в направлении . В пересечении указанных линий получим точку d, которую соединим с полюсом π и получим отрезок [πd], изображающий .

Точку S₄ находим по теореме подобия.

Поскольку , тогда .

Соединив точки π и получим отрезок [π ], соответствующий ускорению .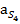

Из плана скоростей находим линейные и угловые ускорения

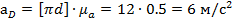
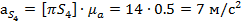
Направление углового ускорения звена 3 получим, поместив вектор тангенциального ускорения в точку В и рассмотрев поворот точки В относительно точки А. Аналогично определяем направление углового ускорения звена 4.

Воспользуйтесь поиском по сайту: