Главные нормальные напряжения

ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ

Основные определения. Тензор напряжения.

В однородном поле напряжение – это сила, которая приходится на единицу площади некоторого сечения, мысленно выделенного в теле. Причем эта сила показывает как действует отброшенная часть тела на оставшуюся.

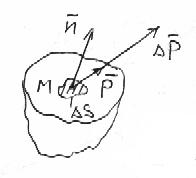На рисунке показана оставшаяся часть тела и вектор силы , которая действует от отброшенной части тела на элемент поверхности сечения , внешняя единичная нормаль к которому . Тогда более точно напряжение, действующее в точке М сечения запишется так

 

 

Рассмотрим в некоторой точке деформируемого тела бесконечно малый тетраэдр. По каждой грани выделенного из тела тетраэдра действуют свои векторы напряжений .

 

Подстрочные индексы показывают, как направлена нормаль к площадке, на которой они действуют (напряжение действует по площадке, нормаль к которой параллельна оси Х и т.д.). Напряжение на наклонной площадке .

 

Каждый из указанных векторов напряжений можно задать его проекциями на координатные оси

 

Здесь второй индекс у указывает координатную ось на которую проецируется напряжение . Величины s_xy, s_xz, s_yx, s_yz, s_zx, s_zy - компоненты векторов напряжений, лежащие в плоскостях граней тетраэдра соответственно ВОС, АОС, АОВ – называются касательными напряжениями. Величины s_xx, s_yy, s_zz – являются компонентами напряжений , перпендикулярными к граням тетраэдра и называются нормальными напряжениями.

Если заданы компоненты напряжений по трем взаимно перпендикулярным площадкам, проходящим через данную точку деформируемого тела, то напряжения на любой площадке, наклонной к координатным плоскостям можно подсчитать по формулам.

(1.1)

Здесь n_x, n_y, n_z – направляющие косинусы наклонной площадки по отношению к координатным плоскостям.

Коэффициенты (напряжения) при направляющих косинусах n_i в уравнениях (1.1.) образуют так называемый тензор напряжения

(1.2)

содержащий шесть существенных компонент, т.к. является симметричным (s_ij = s_ji, т.е. s_xy = s_yx и т.д.).

Главные нормальные напряжения

Инварианты тензора напряжения

Площадки, на которых отсутствуют касательные напряжения, называются площадками главных нормальных напряжений s₁₁, s₂₂, s₃₃. Индексы при последних назначаются по правилу

т.е. индекс "1" присваивается большему, а "3" – меньшему из значений.

Тензор напряжений, записанный в ортогональной системе координат, совпадающей с направлениями главных напряжений, имеет вид

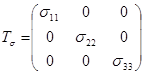(1.3)

Это означает, что напряженное состояние в любой точке деформируемого тела вызвано чистым растяжением или сжатием по трем взаимно перпендикулярным главным направлениям.

Главные напряжения являются корнями кубического уравнения

(1.4)

Коэффициенты 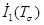, , этого уравнения называются инвариантами тензора напряжений. В произвольной ортогональной системе координат и ортогональной системе координат, совпадающей с направлениями главных нормальных напряжений они имеют вид

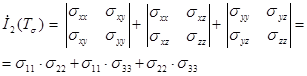(1.5)

Величина, составленная из первого инварианта

(1.6)

называется средним (или гидростатическим) давлением в точке и имеет большое значение в теории пластичности и теории ОМД. В тензорной форме она записывается так:

 

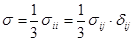
Девиатор тензора напряжения и его инварианты

Так как материалы обладают, как правило, различными механическими свойствами по отношению к сдвигу и равномерному всестороннему сжатию, целесообразно представить тензор напряжения в виде суммы двух тензоров

(1.7)

Здесь s × Е – так называемый шаровой тензор, соответствующий среднему давлению в некоторой точке деформируемого тела и отвечающий за изменение его объема.

, (Е - единичный тензор)

а 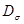– тензор, характеризующий касательные напряжения в той же точке, называется девиатором напряжения и отвечает за изменение формы. Он характеризует насколько заданное напряженное состояние отличается от всестороннего равного растяжения или сжатия с главными напряжениями равными s.

Главные направления девиатора напряжения 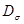и тензора напряжения Т_s совпадают, а главные значения S₁₁, S₂₂, S₃₃ отличаются от s₁₁, б₂₂, s₃₃ на величину среднего давления s.

Компоненты девиатора 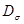будем обозначать через S_ij. Тогда компоненты тензора Т_s можно представить через компоненты девиатора 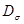и шарового тензора s × Е так:

(1.8)

Инварианты девиатора напряжения имеют вид:

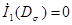
(1.9)

Большую роль в теории пластичности играет второй инвариант. Неотрицательную величину

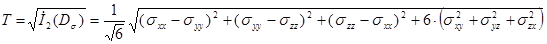(1.10)

называют интенсивностью касательных напряжений. В главных напряжениях она имеет вид

(1.11)

В тензорной форме она запишется так

(1.12)

Интенсивность касательных напряжений обращается в нуль, когда напряженное состояние является состоянием гидростатического давления

Для чистого сдвига

; ;

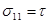Здесь t – напряжение чистого сдвига. Следовательно

В случае одноосного растяжения (сжатия) в направлении, например, оси Х

 

; ;

Тогда

(1.13)

 

 

Поделиться:

Воспользуйтесь поиском по сайту: