 |
Понятия об оптимизации. Целевая функция.
|
|
|
|
Вопрос №9.
Уравнение регрессии. Метод наименьших квадратов и его использование для нахождения коэффицентов для уравнения регрессии.
 (уравнение регрессии в общем виде).
(уравнение регрессии в общем виде).
Метод наименьших квадратов — математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных.
Коэфиценты уравнения определяется методом наименьших квадратов из условия:

Где N – объем выборки из всей совокупности значений исследуемых параметром. Разность между объемом выборки N и числом связей наложенных на эту выборку l, называется числом степеней свободной выборки f. f=N-l.
Вопрос №10.
Статистический анализ полученных математических моделей. Дисперсия воспроизводимости, Дисперсия остаточная, критерий Стьюдента, критерий Фишера.
Статистический анализ полученных математических моделей- Основу их состовляет отображение явлений и процессов с помощью случайных событий и их поведений, которые описываются соответствующими вероятностными характеристиками и статистическими закономерностями.
Дисперсия воспроизводимости необходимая для оценки значимости коэффицентов уравнения регрессии. Число степеней свободы этой дисперсии f равно f=N(m-1)

Остаточная дисперсия определяется разбросом точек корреляционного поля относительно линии регрессии.

Критерий Фишера
F - критерий Фишера является параметричесикм критерием и используется для сравнения дисперсий двух вариационных рядов. Эмпирическое значение критерия вычисляется по формуле:
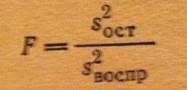
Критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
|
|
|

t-статистика строится обычно по следующему общему принципу: в числителе случайная величина с нулевым математическим ожиданием (при выполнении нулевой гипотезы), а в знаменателе — выборочное стандартное отклонение этой случайной величины, получаемое как квадратный корень из несмещенной оценки дисперсии.
Вопрос №11
Понятия об оптимизации. Целевая функция.
Оптимизация —задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Методы оптимизации классифицируют в соответствии с задачами оптимизации:
Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.
Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.
Целевая функция - Функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.
В широком смысле целевая функция есть математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим. Примером критерия в теории статистических решений является среднеквадратический критерий точности аппроксимации.
Цель – найти такие оценки, при которых целевая функция достигает минимума.Важно, что критерий всегда привносится извне, и только после этого ищется правило решения, минимизирующее или максимизирующее целевую функцию.
|
|
|
Вопрос № 12
|
|
|


