 |
Предметная интерпретация асинхронного процесса
|
|
|
|
Содержание
1. Постановка задачи
2. Описание процесса
3. Построение метамодели "асинхронный процесс"
4. Операции над процессами
4.1 Репозиция
4.2 Редукция
4.3 Композиция процессов
5. Предметная интерпретация асинхронного процесса
5.1 Сеть Петри (для процесса подготовки к вырезанию)
Заключение
Постановка задачи
1. Выбрать вычислительный процесс и на его примере:
- построить метамодель "асинхронный процесс" и определить свойства исходного процесса на основе анализа метамодели;
- выполнить операции над процессом: репозиция, редукция, композиция, и оценить полученные результаты с практической точки зрения;
- построить предметную интерпретацию метамодели на основе сети Петри и сделать вывод о динамических характеристиках исходного процесса.
2. Оформить отчет.
Описание процесса
Предлагается рассмотреть процессы и ситуации для плоттера. Существуют плоттеры двух видов: печатающие и режущие. В данной работе будет рассматриваться режущий плоттер. Режущий плоттер - это устройство, вырезающее/прорисовывающее векторный контур на специальном материале. Наиболее важные части устройства - это подвижный зажим для ножа/карандаша, двигающийся только горизонтально; нож/карандаш, двигающийся только вертикально; диодные датчики, фиксирующие наличие материала в устройстве; вращающиеся валики/ зажимы, позволяющие закреплять материал, а также передвигающие его в одном направлении.
3. Построение метамодели "асинхронный процесс"
Асинхронным процессом называется процесс 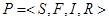 , где S - Множество ситуаций, возможных в процессе, F - Отношение непосредственного следования ситуаций, определенное на множестве этих ситуаций, I - Множество инициаторов - множество ситуаций из S, для которых имеет место:
, где S - Множество ситуаций, возможных в процессе, F - Отношение непосредственного следования ситуаций, определенное на множестве этих ситуаций, I - Множество инициаторов - множество ситуаций из S, для которых имеет место: 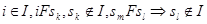 , R - множество результантов - таких ситуаций из S, что
, R - множество результантов - таких ситуаций из S, что 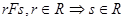 . Под ситуацией понимается сочетание условий и обстоятельств, создающих определенную обстановку или положение. Инициаторы - ситуации, являющиеся подмножествами множества ситуаций, которые активизируют процесс. Особенностью инициаторов является то что они не могут быть только следствием некоторого подмножества ситуаций, они обязательно должны быть причиной. Результанты - подмножество множества ситуаций, состоящее из финальных ситуаций. Особенностью результантов является то что они не могут быть только причиной некоторого подмножества ситуаций, они обязательно должны быть следствием какой-то причины.
. Под ситуацией понимается сочетание условий и обстоятельств, создающих определенную обстановку или положение. Инициаторы - ситуации, являющиеся подмножествами множества ситуаций, которые активизируют процесс. Особенностью инициаторов является то что они не могут быть только следствием некоторого подмножества ситуаций, они обязательно должны быть причиной. Результанты - подмножество множества ситуаций, состоящее из финальных ситуаций. Особенностью результантов является то что они не могут быть только причиной некоторого подмножества ситуаций, они обязательно должны быть следствием какой-то причины.
|
|
|
Плоттер.
1. A - микроконтроллер
+ - запущен
бездействует
. Z - Подвижный зажим ножа
+ - двигается
бездействует
. K - нож/карандаж
+ - опущен
поднят
. V - система подвижных зубчатых валиков
+ - двигаются
бездействуют
. D - диодные датчики
+ - активны
не активны
. M - память
+ - выделена
пуста
. L - материал для резки/ нанесения контура
+ - имеется
отсутствует
Все возможные ситуации:
1) Плоттер полностью готов к выполнению задания (находится в режиме ожидания):
A+ Z - K+ V - D+ M - L+
2) В буфер памяти поступила информация:
A+ Z - K+ V - D+ M+ L+
) Начинается прогонка материала для нахождения начальной точки прорезания:
A+ Z+ K - V+ D+ M+ L+
) Вылет материала из плоттера (error):
A+ Z+ K - V+ D - M+ L-
) Вырезание/прорисовка контура на материале:
A+ Z+ K+ V+ D+ M+ L+
 (1,0,1,0,1,0,1)
(1,0,1,0,1,0,1)
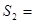 (1,0,1,0,1,1,1)
(1,0,1,0,1,1,1)
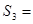 (1,1,0,1,1,1,1)
(1,1,0,1,1,1,1)
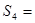 (1,1,0,1,0,1,0)
(1,1,0,1,0,1,0)
 (1,1,1,1,1,1,1)
(1,1,1,1,1,1,1)
Граф, отображающий процесс резки/прорисовки контура:
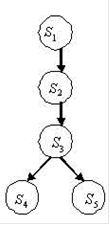

I={  ,
, 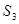 }-инициаторы;
}-инициаторы;
Ситуация  (готовность принтера) является инициатором ко всем дальнейшим ситуациям. Эта ситуация является своего рода стартом ко всему процессу.
(готовность принтера) является инициатором ко всем дальнейшим ситуациям. Эта ситуация является своего рода стартом ко всему процессу.
|
|
|
Ситуация 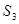 является инициатором к ситуациям, описывающим непосредственно финальную работу плоттера, т.е. резку контура, а также возможную ошибку. Две последние и являются результантами (
является инициатором к ситуациям, описывающим непосредственно финальную работу плоттера, т.е. резку контура, а также возможную ошибку. Две последние и являются результантами (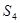 и
и  ).
).
R={ 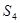 ,
, 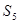 } - результанты;
} - результанты;
Классы эквивалентности:
Начальный класс - 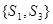 ;
;
Заключительные классы - 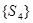 ,
, 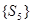 ;
;
Траектории - 
Первая траектория описывает полную подготовленность плоттера к резке, вывод данных в память плоттера, начало резки (прогонку материала) и ошибку при начале резки, т.е. вылет материала из плоттера.
Вторая траектория описывает вывод данных в память плоттера, начало резки и ее нормальное безошибочное продолжение.
Остальные две траектории описывают непосредственно начало процесса резки, с нормальным продолжением и с ошибкой.
Выводы:
После построения модели АП для данного процесса можно утверждать, что:
т.к. из инициаторов все траектории ведут в результанты, и каждая из траекторий, приводящая к результантам, начинается в каком-либо инициаторе, данный АП является эффективным;
вследствие того, что, траектории из инициаторов ведут в различные заключительные классы 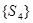 ,
, 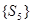 (существует неопределённость), данный АП не является управляемым;
(существует неопределённость), данный АП не является управляемым;
в результате того, что, из инициатора  можно попасть в другой инициатор
можно попасть в другой инициатор  (а это противоречит условию:
(а это противоречит условию: 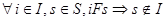 ), данный АП не является простым.
), данный АП не является простым.
Операции над процессами
Репозиция
Репозицией асинхронного процесса  называется эффективный асинхронный процесс
называется эффективный асинхронный процесс 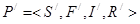 , такой что
, такой что 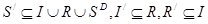 Ситуации
Ситуации 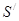 репозиции может содержать только те ситуации из исходного процесса, которые являются инициаторами или результантами некоторой дополнительной ситуации из множества
репозиции может содержать только те ситуации из исходного процесса, которые являются инициаторами или результантами некоторой дополнительной ситуации из множества 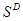 . Отношение
. Отношение 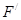 задает траектории перехода от элементов из
задает траектории перехода от элементов из  к элементам из R', возможно через дополнительные ситуации из
к элементам из R', возможно через дополнительные ситуации из  .
.
Иными словами репозиция - это не что иное как возобновление процесса, его повторение.
В случае с плоттером, репозицией будет являться прорезание/ прорисовывание нового контура на одном и том же материале.
Инициатором будет ситуация 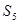 , а результантом
, а результантом 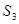 . Ввод дополнительных ситуаций не требуется.
. Ввод дополнительных ситуаций не требуется.
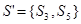
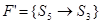
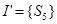 ,
, 
Граф репозиции данного процесса:

Вывод:
Отношение  задаёт траектории переходов от элементов из множества
задаёт траектории переходов от элементов из множества  к элементам множества
к элементам множества 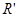 . Так как
. Так как 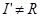 ,
, 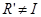 и
и 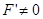 , то репозиция является частичной.
, то репозиция является частичной.
|
|
|
Редукция
Пусть дан асинхронный процесс P = (S, F, I, R), ситуации которого структурированы по второму способу, то есть по входным и выходным компонентам: s = (x, y, z). Образуем p-блочное разбиение множества ситуаций S процесса P, в ситуациях каждого блока которого входная компонента xj принимает фиксированное значение (1 £ j £ p). Выбираем r (r < p) различных значений входной компоненты и составим множество X* Ì X (X - множество входных компонент). Ситуации, входящие в блоки разбиения, которые соответствуют выбранным значениям входной компоненты, составят подмножество S*. Для каждого инициатора si Î I построим множество ситуаций S (si), встречающихся на траекториях, ведущих из si. Образуем множество S (X*) как объединение тех множеств S (si), для которых справедливо S (si) Í S*. На базе этого множества S (X*) выделяем инициаторы, результанты и отношения:
F (X*) = F Ç (S (X*) ´ S (X*));(X*) = I Ç S (X*); (X*) = R Ç S (X*).
Назовем построенный таким образом процесс P (X*) = (S (X*), F (X*), I (X*), R (X*)) редукцией асинхронного процесса P = (S, F, I, R) по выбранному множеству X* значений входной компоненты.
Редукция позволяет выделить отдельные ветви процесса, что характерно при рассмотрении отдельных ситуаций. Таким образом, редукция может быть полезна для изучения отдельных элементов процесса.
Постараемся выделить ветвь процесса, характеризующую непосредственно резку контура плоттером.
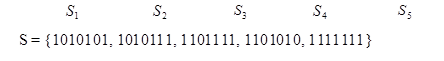
I={ 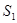 ,
, 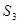 }
}
R={ 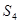 ,
, 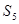 }
}

Выделим входную компоненту X={01,10,11} из второго и третьего элементов векторов ситуаций. Эти компоненты выбраны неслучайно. Именно по ним можно идентифицировать интересующий нас подпроцесс.
Выберем 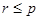 различных значений входной компоненты:
различных значений входной компоненты: 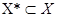 . X*={10,11}. В данном случае отбрасывается первый элемент вектора X потому что он идентифицирует не интересующие нас ситуации.
. X*={10,11}. В данном случае отбрасывается первый элемент вектора X потому что он идентифицирует не интересующие нас ситуации.
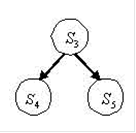
Тогда редукцией P (X*) будет являться:
S* = { 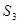 ,
, 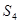 ,
, 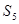 };
};
S (X*) ={ 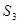 ,
, 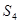 ,
, 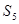 }; Ситуации, которые лежат внутри траекторий основного процесса и входят в S*.
}; Ситуации, которые лежат внутри траекторий основного процесса и входят в S*.
F (X*): 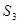 ->
-> 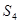 ;
; 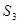 ->
-> 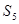 ;(X*) ={
;(X*) ={ 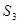 }; R (X*) ={
}; R (X*) ={ 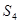 ,
,  };
};
|
|
|
Граф редукции:
Композиция процессов
Рассмотрим два асинхронных процесса 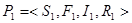 не обязательно приведенный процесс и
не обязательно приведенный процесс и 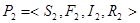 приведенный процесс. Ситуации, которых структурированы следующим образом:
приведенный процесс. Ситуации, которых структурированы следующим образом:
В  выделена выходная, а в
выделена выходная, а в 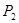 входная компоненты. Пусть все или некоторые значения выходной компоненты ситуации
входная компоненты. Пусть все или некоторые значения выходной компоненты ситуации  соответствуют всем или некоторым компонентам ситуации
соответствуют всем или некоторым компонентам ситуации 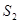 . Обозначим проекции множества пар соответствующих друг другу значений компоненты на множество
. Обозначим проекции множества пар соответствующих друг другу значений компоненты на множество  и множество
и множество  соответственно. По множествам
соответственно. По множествам  и
и  построим редукции
построим редукции 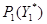 и
и 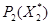 . Пусть
. Пусть 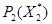 оказывается полностью приведенным, тогда множество ситуаций приведенного процесса совпадают с выделенными компонентами
оказывается полностью приведенным, тогда множество ситуаций приведенного процесса совпадают с выделенными компонентами 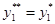 ,
,  . Множество, по которому производится редукция совпадает полностью с множеством выделенных компонент. Построим, если это возможно процесс
. Множество, по которому производится редукция совпадает полностью с множеством выделенных компонент. Построим, если это возможно процесс 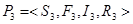 , ситуации которого представимы в виде пар:
, ситуации которого представимы в виде пар: 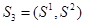 , такой, что:
, такой, что:
) 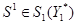 ,
,  :
: 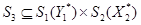 .
.
) выходная компонента 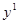 ситуации
ситуации  равна входной компоненте
равна входной компоненте 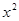 ситуации
ситуации  .
.
) если в  компонента
компонента  , то
, то 
) если некоторые ситуации из  :
:
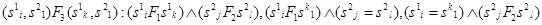
Назовем последовательной композицией асинхронных процессов  и
и 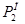 асинхронный процесс
асинхронный процесс 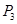 , образованный отождествлением значений входной и выходной компонент ситуаций редуцированных процессов
, образованный отождествлением значений входной и выходной компонент ситуаций редуцированных процессов 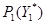 и
и 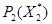 при выполнении перечисленных выше ограничений. Смысл первого ограничения состоит в том, чтобы при функционировании процесса
при выполнении перечисленных выше ограничений. Смысл первого ограничения состоит в том, чтобы при функционировании процесса 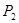 в составе
в составе 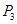 в его редукции не встретились ситуации не принадлежащие множеству
в его редукции не встретились ситуации не принадлежащие множеству 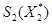 . Смысл второго ограничения состоит в том, чтобы для редукции
. Смысл второго ограничения состоит в том, чтобы для редукции 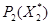 в составе процесса
в составе процесса 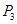 не может возникнуть новая траектория.
не может возникнуть новая траектория.
Возьмем рассматриваемый процесс резки/ прорисовки контура на плоттере (обозначим его за P1) и обьединим его с процессом к его подготовки (обозначим как P2). Тогда в P1 войдут ситуации 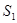 -
- 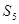 (переобозначим их на
(переобозначим их на 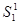 -
-  ), а в P2 ситуации
), а в P2 ситуации 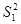 -
- 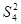 .
.
Рассмотрим подробнее процесс P2:
Компоненты:
1. A - микроконтроллер
+ - запущен
бездействует
. Z - Подвижный зажим ножа
+ - двигается
бездействует
. D - диодные датчики
+ - активны
не активны
. L - материал для резки/ нанесения контура
+ - имеется
отсутствует
Ситуации:
) Плоттер включен, память пуста, материала нет:
A+ Z - D - L-
) Материал не попадает на диодные датчики (error):
A+ Z - D - L+
) Плоттер включен с приготовленным материалом:
A+ Z - D+ L+
4) Плоттер фиксирует точку отсчета для готовности к работе:
A+ Z+D+ L+
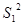 = (1,0,0,0)
= (1,0,0,0)
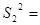 (1,0,0,1)
(1,0,0,1)
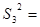 (1,0,1,1)
(1,0,1,1)
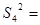 (1,1,1,1)={
(1,1,1,1)={ 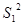 } R={
} R={  ,
, 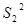 }
}
плоттер асинхронный процесс петри
Граф:

Редукция.
Постараемся выделить ветвь процесса, характеризующую непосредственно фиксирования начальной точки отсчета на приготовленном материале.
|
|
|
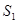
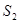
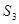
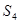
S = {1000, 1001, 1011, 1111}={ 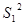 ,
,  ;={
;={  ,
, 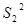 }
}

Выделим входную компоненту X={00,01,11} из второго и третьего элементов векторов ситуаций. Эти компоненты выбраны неслучайно. Именно по ним можно идентифицировать интересующий нас подпроцесс.
Выберем  различных значений входной компоненты:
различных значений входной компоненты: 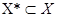 . X*={01,11}. В данном случае отбрасывается первый элемент вектора X потому что он идентифицирует не интересующие нас ситуации.
. X*={01,11}. В данном случае отбрасывается первый элемент вектора X потому что он идентифицирует не интересующие нас ситуации.
Тогда редукцией P (X*) будет являться:
S* =  ; S (X*) =
; S (X*) =  ;
;
Ситуации, которые лежат внутри траекторий основного процесса P2 и входят в S*.
F (X*):  ->
-> 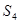 ;
;
I (X*) ={  };
};
R (X*) ={ 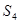 };
};
Граф редукции:
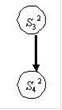
Выделим выходные компоненты процесса P2 и входные компоненты процесса P1, имеющие сходную семантику:
Y= {1} (по первому элементу векторов ситуаций)
X* = {1} (по первому элементу векторов ситуаций)
Построим по ним соответствующие редукции процессов:
S1* = S1 (X*) = S1 = {1010101, 1010111, 1101111, 1101010, 1111111};1 (X*) ={ 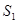 ,
, 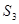 };1 (X*) ={
};1 (X*) ={ 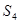 ,
, 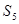 };1* = F1:
};1* = F1:  2* = S2 (Y*) = S2 = {1000, 1001, 1011, 1111};2 (Y*) ={
2* = S2 (Y*) = S2 = {1000, 1001, 1011, 1111};2 (Y*) ={ 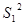 ,
,  ;2 (Y*) ={
;2 (Y*) ={ 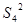 ,
, 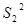 }2* = F2:
}2* = F2: 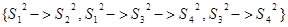
Ситуации процесса P3 представимы в виде пар s3 = (s1, s2) /
1) 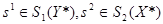
) y1 = x2
) 
) 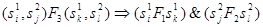 или
или 
или 
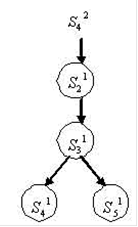
Таким образом, АП P3 = <S3, F3, I3, R3>
S3 = {1111010101, 1111010111, 1111101111, 1111101010, 1111111111}
F3: 1111010101->1111010111->1111101111->1111101010->1111111111
1111010101->1111010111->1111101111->1111101010->11111111113 = {1111010101}
R3 = {1111101010, 1111111111}
Результатом является граф:
Предметная интерпретация асинхронного процесса
|
|
|


