 |
Решение составных задач на дроби.
|
|
|
|
Методика изучения темы «Доли и дроби»
Д о л я – это одна из равных частей целого.
Историческая справка
- Посмотрите, как изображали дробь в Древнем Египте.
- В Древнем Китае вместо черты использовали точку. 
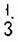
Дроби на Руси называли долями, позднее ломаными числами. В старых руководствах находим следующие названия дробей:
половина полтины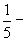 
пятина 
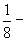полчеть 
полполчеть
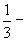треть 
полтреть 
десятина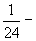 
полполполтреть 
четь 
седьмина 
полполтреть 
полполполчеть (малая четь)
Тема изучается в два этапа: в концентре «Сотня» и «Многозначные числа».
Основные задачи при изучении темы:
1. Создать яркое, конкретное представление о процессе получения долей и дробей.
2. Научить детей записывать, читать и сравнивать доли и дроби.
3. Научить решать задачи двух видов:
- нахождение доли (дроби) числа;
- нахождение числа по доле.
Н а г л я д но с т ь:
Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Как показал опыт, наиболее удобными пособиями являются геометрические фигуры, вырезанные из бумаги; можно использовать рисунки фигур, выполненные на бумаге или в диапозитивах (круги, прямоугольники, треугольники, отрезки и т.п.). Очень важно, чтобы пособия были не только у учителя, но и у каждого из учащихся. Правильные представления о долях, а позднее о дробях будут сформированы тогда, когда ученики будут своими руками получать, например, половину круга, квадрата, и т.п.
Э т а п ы и з у ч е н и я:
1. Образование долей, чтение и запись (М3, ч. 1, с. 80).
Образование долей
Рассмотрим на примере ½ доли. У каждого ученика на уроке по несколько одинаковых кругов, прямоугольников, квадратов, полосок.
|
|
|
- Возьмите 2 круга, один положите перед собой, а другой сложите пополам (учитель показывает, как надо перегнуть и как разрезать круг)
- Это целый круг, а это половина круга, иначе говоря, одна вторая доля круга. Сколько вторых долей в целом круге? (2). Покажите их.
- Возьмите квадрат. Как получить одну вторую долю или половину квадрата? (разделить его на две равные части и взять одну такую часть) Выполняйте.
Аналогично поступают с двумя полосками и делается о б о б щ е н и е:
- Как получали ½ долю круга (квадрата, полоски)? (Разрезали на две равные части и взяли одну такую часть).
Запись и чтение долей
Учительпоказывает готовую карточку.
- Доли записывают с помощью двух цифр. Сначала пишут в одной клеточке цифру 1, затем проводят черту и пишут под чертой цифру 2.
- Число под чертой показывает, на сколько равных частей разделили целое, а число над чертой 1 показывает, что взяли одну такую часть. (Обозначение доли записывают на половине круга (квадрата).
Далее учим читать. Аналогично вводятся 
и 
, 
и 
, 
и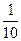 
.
Методические указания
1. При введении названия долей нужно установить связь между названием доли и тем, на сколько равных частей разделили целое.
2. Пособия должны быть индивидуальные и демонстрационные.
3. При делении нужно использовать различные пути деления на равные части (по форме разные, а доля одинаковая).
 |
4. При делении на части, особенно при введении, необходимо использовать образ целого.
Для закрепления этих знаний и умений учащимся предлагают различные упражнения.
Это прежде всего упражнения в назывании и записи долей.
Задание 2. Отметьте 
– квадрата.
Задание 3. Назовите и запишите, какая доля полоски, квадрата, круга закрашена.
 |
Можно предлагать самим детям изобразить к.л. долю отрезка и записать эту долю. В каждом случае надо спрашивать, сколько всего долей в целом. Например, сколько третьих долей отрезка во всем отрезке и т.п.
|
|
|
Практическая работа
Каждому ученику предлагается индивидуальная карточка для самостоятельной работы (один ученик выходит к доске и работает с таким же демонстрационным пособием, можно предложить индивидуальную доску).
 |
Обозначь каждую из закрашенных долей прямоугольника.
Сравнение долей
Эффективным упражнением для формирования представлений о долях является сравнение долей одной и той же величины, которое выполняется чисто практически, с помощью наглядных пособий.
Например, предлагается сравнить доли 
и и поставить знак “>”, ”<”.
Учащиеся изображают доли, например, с помощью отрезков. Сравнивают их и убеждаются, что 1/2больше, чем 1/4.
1/2
1/4
|
> , <
|
> , <
В результате многократного выполнения упражнений подводим детей к обобщению, что чем на большее число мы делим целое, тем меньшая доля у нас получается.
3. З а д а ч и (М3, ч. 1, с. 84):
1 вид. Нахождение доли числа
Решение задач на нахождение доли числа и числа по его доле также способствует формированию представлений о долях величины. В этом их основное назначение. Поэтому, решение задач на нахождение доли числа и числа по его доле выполняется на наглядной основе.
В 3 классе рассматривается только простые задачи, а в четвертом классе они включаются в составные.
Для ознакомления с решением задач лучше предлагать задачи, которые легко иллюстрировать.
| Задача | От полоски длиной 12 см отрезали ¼ ее длины. Чему равна длина ¼ полоски? | |||
| Способ решения | Сначала задачу можно решить графически (практически), а затем подводим к действию делению.
Выясняем сначала, как найти ¼ полоски (разделить ее на 4 равные части и взять одну такую часть). Делим 12 на 4 равные части: 12: 4 = 3 (см) Задача решается на основе конкретного смысла деления и сводится к задаче на нахождение частного в случае деления на равные части.
|
Первой рассматривается задача с непрерывной величиной – длиной, а последующие задачи берутся с дискретными множествами.
|
|
|
«В классе 35 учеников. Плаванием занимается всех учащихся. Сколько человек занимается плаванием?»
«В книге 60 страниц. Мальчик прочитал книги. Сколько страниц прочитал мальчик?»
2 вид. Нахождение числа по доле
| Задача | Длина полоски равна 4 см. Какова длина всей полоски?
| |||
| Способ решения |
По краткой записи повторяем условие задачи.
- Сколько таких долей в целой полоске? (3).
- Как изобразить всю полоску? (Нарисовать 3 раза по 4 см). Сколько таких долей надо причертить еще, чтобы получить всю полоску? Причертим.
- Как же узнать длину всей полоски? (По 4 см взять три раза).
4 × 3 = 12 (см)
 4 см
Т.к. задача является обратной к нахождению доли числа, то можно решить сначала прямую, а затем преобразовать в обратную.
12 см
Эти задачи сводятся к нахождению произведения как суммы одинаковых слагаемых. |
3 смПоследующие задачи решаются с дискретными множествами. Далее задачи двух видов включаются парами и предлагаются как для устного, так и для письменного решения.
1) «У Саши 20 марок. марок он подарил. Сколько марок он подарил?»
2) «У Саши 5 марок с портретами писателей. Они составляют всех его марок. Сколько всего марок у Саши?»
5. Образование дробей (М4, ч.2, с. 109).
Дробь – это одна или несколько равных частей целого.
Двоякий смысл дроби:
1) 
- три четвертых доли от целого
2) Дробь есть результат деления: 3: 4 =
В начальной школе у детей формируется только первый конкретный смысл дроби.
Образование дробей, как и образование долей рассматривается с помощью наглядных пособий.
- Разделите круг на 4 равные части. Как назвать каждую такую часть? Запишите.
- Покажите три четвертые доли. Вы получили дробь - три четвертых. Кто сможет записать эту дробь?
- Что показывает число 4 (на сколько равных частей разделили круг)? Что показывает число 3 (сколько таких частей взяли)?
Аналогичным образом учащиеся получают и записывают другие дроби, объясняя, что показывает каждое число.
|
|
|
Для закрепления полученных знаний выполняются такие же упражнения, как и при ознакомлении с долями: по данным иллюстрациям называют и записывают, какие дроби изображены, или же изображают дробь с помощью чертежа, рисунка.
6. Сравнение дробей (М4, ч.2, с. 109).
Уяснению конкретного смысла дроби помогают упражнения на сравнение дробей. Для сравнения дробей обычно используются иллюстрации с равными прямоугольниками
Здесь можно выделить группы дробей:
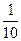1) ; ; 2) ; ; 3) ; ; 
.
Для каждой группы дробей следует изготовить индивидуальные и демонстрационные пособия. Например:
| 1/2 | 1/2 | ||||||
| 1/4 | 1/4 | 1/4 | 1/4 | ||||
| 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 |
Учащимся предлагают начертить в тетради прямоугольник, длина которого 16 см, а ширина 1 см.
- Это один прямоугольник. Запишем (в первом прямоугольнике записывают число 1).
- Начертите под первым прямоугольником такой же второй и разделите его на 2 равные части (выполняют).
- Какие доли получили (вторые, половины). Сколько вторых долей в целом прямоугольнике? Подпишите.
- Ниже начертите такой же прямоугольник и разделите его на 4 равные части. Как называется каждая часть? Сколько четвертых долей в целом прямоугольнике? Сколько четвертых долей в половине?
- Что больше: одна вторая или две четвертые? Начертите четвертый такой же прямоугольник и разделите его на 8 равных частей.
- Как называются полученные доли? Сколько восьмых долей в целом? Сколько восьмых долей в четверти, в половине прямоугольника?
- Что больше: три восьмых или одна четвертая? Какой дроби равна одна вторая?
Ответы на все перечисленные вопросы дети дают, глядя на рисунок.
Предлагаются специальные вопросы на сравнение дробей:
1. Вставьте пропущенный знак ” > “, “ < “ или “ = “
… 
… 1 
…
2. Подбираете такое число, чтобы равенство (неравенство) было верным:
= 
= 
=
Выполняя такие и подобные упражнения, учащиеся прибегают к соответствующим иллюстрациям с прямоугольниками, или заново изображают дроби с помощью, например отрезков.
3. М4, ч. 2, с. 37, № 181.
7. Введение задачи на нахождение дроби от числа (М4, ч.1, с. 47).
Конкретный смысл дроби очень ярко раскрывается при решении задач на нахождение дроби числа. Решение этих задач, как и задач на нахождение доли числа, выполняется с помощью соответствующих наглядных пособий.
|
этого отрезка?»
10 см
1) Найдем, сколько сантиметров в одной пятой доле отрезка: 10: 5 = 2 (см).
2) Найдем, сколько сантиметров в четырех пятых долях отрезка: 2 × 4 = 8 (см).
Два действия можно записать одним выражением: 10: 5 × 4 = 8 (см).
|
|
|
Далее включаются задачи с дискретными множествами. Задачи на нахождение дроби числа должны предлагаться для устного и письменного решения.
Решение составных задач на дроби.
1) М4, ч. 1, с. 82, № 415
«Рабочие должны были посадить 350 саженцев. В первый день они посадили одну седьмую часть всех саженцев, а во второй день – три седьмых всех саженцев».
Поставь вопрос и реши задачу.
2) М4, ч. 21, с. 14, № 77
«Молочный завод отправил в магазин 56 ящиков сливочного масла, по 20 кг в каждом. За день продали две пятые части этого масла. Сколько килограммов масла осталось?»
3) М4, ч. 2 с. 15, № 4
«Для ремонта квартиры купили 8 рулонов обоев, длиной по 10 м 50 см. Израсходовали три четвертых части купленных рулонов обоев. Сколько метров обоев осталось?
4) М4, ч. 2 с. 15, № 5
«Школьная библиотека получила 3420 новых учебников. Что составило одну десятую часть всех уже имевшихся в библиотеке учебников. Сколько учебников стало в школьной библиотеке?»
5) М4, ч. 2 с. 51, № 252
«Масса угля в железнодорожном вагоне 60 т. Самосвал может взять три десятые части этого угля. Сколько рейсов надо сделать на самосвале, чтобы разгрузить 6 таких вагонов?»
|
|
|
