 |
АРПСС позволяет анализировать временные ряды с сезонностью. В данном случае удобно взять модель со следующими параметрами.
|
|
|
|
Статистический анализ и прогнозирование авиаперевозок
Содержание
Постановка задачи
Разведочный анализ
Визуальный анализ
Выделение периодичности
Исследование свойств ряда
Прогноз АРПСС
Проверка качества прогноза
Прогноз моделью экспоненциального сглаживания
Выводы
Список литературы
Постановка задачи
Рассмотрим задачу построения прогноза авиаперевозок США по историческим данным. Данные взяты с ресурса www.bts.gov и представляют собой помесячное количество пассажиров в период с января 2003 года по декабрь 2009 года.
Количество пассажиров измеряется в миллионах человек.

Табл. 1. Фрагмент исходных данных
Цель исследования – спрогнозировать перелеты по месяцам на 2010 год.
Разведочный анализ
Визуальный анализ
Построим линейный график временного ряда (см. рис. 1).
Данные обладают ярко выраженной сезонной структурой.
Как видим, максимумы интенсивности авиаперевозок приходятся на июль.

Рис. 1. Линейный график количества пассажиров
Выделение периодичности
Для выявления периодичности применим спектральный анализ. Этот метод можно использовать для подтверждения нашей гипотезы о том, что ряд обладает сезонной структурой. Предполагаемый период сезонного цикла – 12 месяцев.
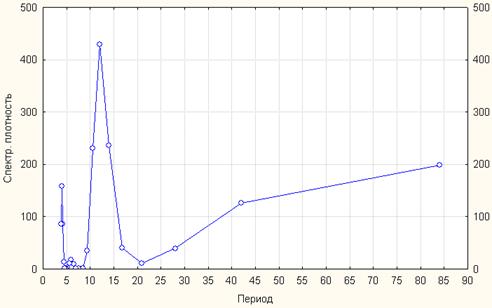
Рис. 2. График спектральной плотности
На графике спектральной плотности видим, что наибольшее значение плотности соответствует периоду 12 месяцев, из линейного графика видно, что повторяющиеся пики соответствуют месяцу июль, т.е. повторяются через 12 месяцев.
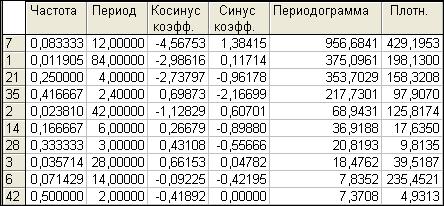
Табл. 2. Наибольшие значения перидиограммы
|
|
|
Исследование свойств ряда
Вид автокорреляционной функции позволяет нам определить, какие параметры прогностической модели АРПСС нужно взять.
Автокорреляционная функция для данного ряда будет иметь вид:
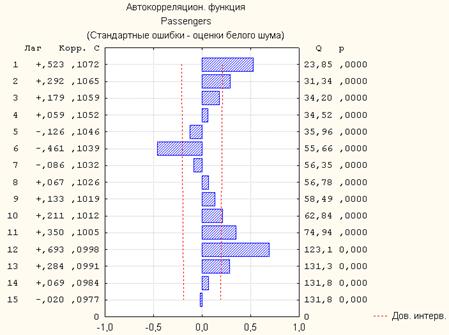
Рис. 3. Автокорреляционная функция для исходного ряда
График показывает сильную периодическую зависимость между компонентами ряда: автокорреляции на лагах 1, 12 имеют максимальные значения.
Прологарифмируем ряд, чтобы сгладить скачки амплитуды, для последующего анализа с помощью автокорреляционных функций.
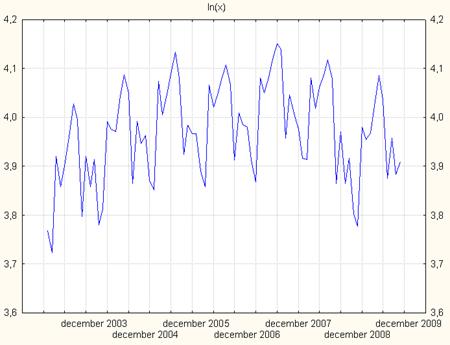
Рис. 4. Прологарифмированный временной ряд
Автокорреляционная функция преобразованного ряда поможет нам более чётко увидеть временные зависимости в нашем ряду:
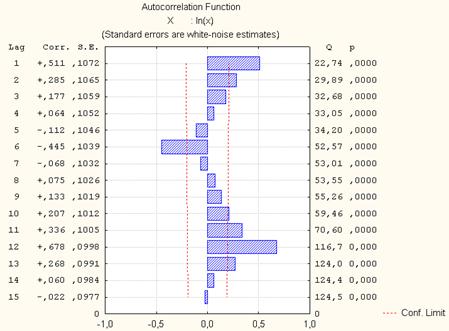
Рис. 5. Автокорреляционная функция для прологарифмированного ряда
Автокорреляция имеет ярко выраженный периодический характер. Причем автокорреляция на лагах 1,12 имеет максимальные значения.
От преобразованного ряда возьмём разности с лагом 1.
После логарифмирования ряда и взятия разностей с лагом 1 получаем такую автокорреляционную картину:

Рис. 6. Автокорреляционная функция после взятия разности с лагом 1
Теперь возьмём разность с лагом 12:
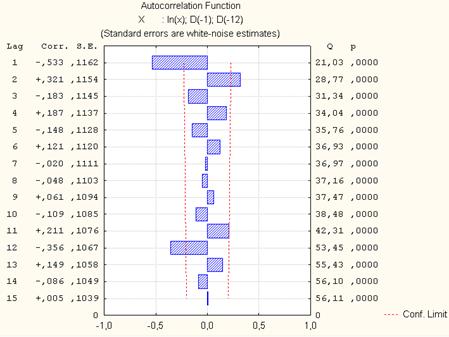
Рис. 7. Автокорреляционная функция после взятия разности с лагом 12
Большинство сильных автокорреляций теперь удалено.
Построим частную автокорреляционную функцию для нашего нового ряда.
В случае, когда лаги на ней будут независимы, можно говорить о том, что ряд поддается анализу АРПСС. Частная автокорреляционная функция будет иметь вид:

Рис. 8. Частичная автокорреляционная функция
Прогноз АРПСС
В этом разделе для построения прогноза мы будем использовать линейную математическую модель авторегрессии и проинтегрированного скользящего среднего (АРПСС).
Подобрать наилучшую модель АРПСС можно путем перебора моделей с различными параметрами, применяя для их сравнения метод кросс-проверки (cross-validation).
|
|
|
АРПСС позволяет анализировать временные ряды с сезонностью. В данном случае удобно взять модель со следующими параметрами.
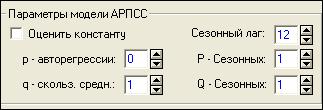
Рис. 9. Параметры модели АРПСС
|
|
|


