 |
Задачи по ООП для 333 группы
|
|
|
|
Раздел 1. Знакомство с основными конструкциями C++
1.1. Из заданного множества точек на плоскости выбрать две различные точки так, чтобы количества точек, лежащих по разные стороны прямой, проходящей через эти две точки, различались наименьшим образом.
1.2. Определить радиус и центр окружности, на которой лежит наибольшее число точек заданного на плоскости множества точек.
1.3. Задано множество М точек на плоскости. Определить, верно ли, что для каждой точки А 
М существует точка В М (А 
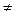В) такая, что не существует двух точек множества М, лежащих по разные стороны от прямой АВ.
1.4. Определить радиус и центр такой окружности, проходящей хотя бы через три различные точки заданного множества точек на плоскости, что минимальна разность количества точек, лежащих внутри и вне окружности.
1.5. Многоугольник (не обязательно выпуклый) задан на плоскости перечислением координат вершин в порядке обхода его границы. Определить площадь многоугольника.
1.6. Задано множество прямых на плоскости (коэффициентами своих уравнений). Подсчитать количество точек пересечения этих прямых.
1.7. Порядок на точках плоскости определим следующим образом: (x, y) 
(u, 
), если либо x<u, либо x= u и y . Перечислить точки заданного множества точек на плоскости в соответствии с этим порядком.
1.8. На плоскости заданно n множеств по m точек в каждом. Среди точек первого множества найти такую, которая принадлежит наибольшему количеству множеств.
1.9. Выбрать три разные точки заданного на плоскости множества точек, составляющие треугольник наибольшего периметра.
1.10. Из заданного на плоскости множества точек выбрать такие три точки, не лежащие на одной прямой, которые составляют треугольник наименьшей площади.
|
|
|
1.11. Заданно множество точек на плоскости. Выбрать из них четыре разные точки, которые являются вершинами квадрата наибольшего периметра.
1.12. Из заданного множества точек на плоскости выбрать три разные точки А, В, С так, чтобы внутри треугольника АВС содержалось максимальное количество точек этого множества.
1.13. Из заданного на плоскости множества точек выбрать три различные точки так, чтобы разность между площадью круга ограниченного окружностью, проходящей через эти три точки, и площадью треугольника с вершинами в этих точках была минимальной.
1.14. Определить радиус и центр окружности минимального радиуса, проходящей хотя бы через три различные точки заданного множества точек на плоскости.
1.15. Найти такую точку заданного на плоскости множества точек, сумма расстояний от которой до остальных минимальна.
Раздел 2. Обработка символьной информации
2.1. Перечислить все слова заданного предложения, которые состоят из тех же букв, что и первое слово предложения.
2.2. В заданном предложении найти пару слов, из которых одно является обращением другого.
2.3. Для каждого из слов заданного предложения указать, сколько раз оно встречается в предложении.
2.4. Из заданного текста выбрать и напечатать те символы, которые встречаются в нем ровно один раз (в том порядке, как они встречаются в тексте).
2.5. В предложении все слова начинаются с различных букв. Напечатать (если можно) слова предложения в таком порядке, чтобы последняя буква каждого слова совпадала с первой буквой следующего слова.
2.6. Найти множество всех слов, которые встречаются в каждом из двух заданных предложений.
2.7. Отредактировать заданное предложение, удаляя из него все слова с нечетными номерами и переворачивая слова с четными номерами.
2.8. Найти самое длинное общее слово двух заданных предложений.
|
|
|
2.9. Даны два предложения. Найти самое короткое из слов первого предложения, которого нет во втором предложении.
2.10. Напечатать заданное предложение таким образам, чтобы каждое его слово целиком находилось в одной и той же строке распечатки (т.е. избавиться от переносов).
2.11. В заданном предложении указать слово, в котором доля гласных (A, E, I, O, U) максимальна.
2.12. Переставить и распечатать слова заданного предложения в соответствии с ростом доли согласных (B, C, D, F, G, H, K, L, M, N, P, Q, R, S, T, V, W, X, Z) в этих словах.
2.13. Для каждого символа заданного текста указать, сколько раз он встречается в тексте. Сообщение об этом символе должно печататься не более одного раза.
2.14. Отредактировать заданное предложение, удаляя из него все слова, целиком составленные из вхождений не более чем двух букв.
2.15. Задан текст, в котором нет вхождений символов `(`и`)`. Выполнить его сжатие, то есть заменить всякую максимальную подпоследовательность, составленную из более чем трех вхождений одного и того же символа, на (k)s, где s – повторяемый символ, а k>3 – количество его повторений.
2.16. Отредактировать заданное предложение, заменяя всякое вхождение слова вида aba1 на b, где a, b – подслова, a1 - обращение слова a.
Раздел 3. Списки в C++
При решении задач этого раздела создать класс, описывающий элемент списка. Указатель на заглавное звено списка должен принадлежать классу!
Во всех приведенных ниже задачах используйте списки с заглавным звеном.
Построение
3.1. Пусть задан файл f, элементами которого являются целые числа. Написать программу построения из элементов файла f однонаправленного списка.
3.2. Пусть задан файл, элементами которого являются символы. Написать программу построения из элементов файла f однонаправленного списка.
3.3. Пусть задан массив, элементами которого являются целые числа. Написать программу построения из элементов массива X однонаправленного списка.
3.4. Пусть задан массив символов. Написать программу построения из элементов массива X однонаправленного списка.
3.5. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются вещественные числа. Написать программу, которая по списку P строит два новых списка: L1 - из положительных элементов списка P, L2 - из остальных элементов списка P.
|
|
|
3.6. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются вещественные числа. Написать программу, которая по списку P строит два новых списка: L1 - из положительных элементов списка P, L2 - из отрицательных элементов списка P.
3.7*. Написать программу, которая объединяет два упорядоченных по неубыванию списка L1 и L2 в один упорядоченный по неубыванию список путем построения нового списка.
3.8. Многочлен P(x) = an*xn + an-1*xn-1+...+ ao с целыми коэффициентами представьте в виде списка, причем, если ai=0, то соответствующее звено в список не включается.
3.9. Многочлен P(x) = an*xn + an-1*xn-1+...+ ao с целыми коэффициентами представьте в виде списка, причем, если ai=0, то соответствующее звено в список не включается. Описать функцию Dif(p,q), которая строит многочлен p - производную многочлена q.
3.10. Многочлен P(x) = an*xn + an-1*xn-1+...+ ao с целыми коэффициентами представьте в виде списка, причем, если ai=0, то соответствующее звено в список не включается. Описать функцию Add(p,q,r), которая строит многочлен p - сумму многочленов q и r.
3.11*. Задача состоит в чтении некоторого текста, выборе из него слов и подсчете частоты их появления, то есть в составлении частотного словаря. Очевидно, что для этого нужно составить список слов, найденных в тексте. Каждое очередное слово, прочитанное в тексте, ищется в списке. Если слово найдено, счетчик его частоты увеличивается, в противном случае слово добавляется к списку. Чтобы сосредоточить внимание на основной задаче обработки списка, мы предположим, что слова уже выделены из исследуемого текста, закодированы целыми числами и находятся во входном файле.
Модификация
3.12. Разработать функцию для включения данного линейного списка в начало другого линейного списка.
3.13. Разработать функцию для включения данного линейного списка в конец другого линейного списка.
3.14. Разработать функцию для включения данного линейного списка в "середину" другого линейного списка.
|
|
|
3.15. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются символы. Написать программу, которая заменяет в списке P все вхождения элемента Е1 на элемент Е2.
3.16. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются символы. Написать программу, которая меняет местами первый и последний элементы непустого списка P.
3.17. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая позволит вставить новый элемент в начало списка P.
3.18. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая в конец списка P вставляет новый элемент.
3.19. Предположим, что уже построены и заданы указателями L и E однонаправленные списки, элементами которых являются целые числа. Написать программу, которая в непустой список L, элементы которого упорядочены по неубыванию, вставляет новый элемент E так, чтобы сохранилась упорядоченность.
3.20. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая должна из непустого списка P удалить первый элемент, являющийся простым числом.
3.21. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая из списка P удаляет второй четный элемент, если такой есть.
3.22. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая из списка P удаляет первый отрицательный элемент, если он есть.
3.23. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая удаляет из списка P все отрицательные элементы.
3.24. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая должна перенести в конец непустого списка его первый элемент.
3.25. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая должна перенести в начало непустого списка его последний элемент.
3.26. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая из списка P удаляет все вхождения элемента E.
|
|
|
3.27*. Написать функцию поиска элемента с заданным информационным полем в упорядоченном однонаправленном линейном списке следующим образом. Для текста программ характерно частое скопление одного и того же идентификатора, то есть за одним вхождением часто следует одно или более повторных вхождений того же слова. Это наводит на мысль реорганизовать список после каждого обращения, переставляя найденное слово в начало списка, тем самым минимизируя длину прохода по списку при последующем поиске того же слова. Этот метод называется поиском по списку с переупорядочиванием.
3.28*. Рассмотрим пары целых чисел (i,j). Говорят, что пара (i,j) меньше, чем другая пара (h,k) (записывается (i,j)<(h,k)), если либо i<h, либо i=h и j<k. Например, (-1,5)<(5,1)<(5,2). Такой порядок называется лексикографическим упорядочением пар целых чисел. Дан линейный однонаправленный список, содержащий пары целых чисел. Упорядочить его лексикографически по возрастанию пар.
Предикаты
3.29. Предположим, что уже построен однонаправленный список, элементами которого являются символы. Написать программу, которая проверяет, упорядочен ли список по неубыванию (невозрастанию) кодов ASCII.
3.30. Предположим, что уже построен однонаправленный список, элементами которого являются символы. Написать программу, которая проверяет, встречается ли значение первого элемента еще раз в списке.
3.31. Предположим, что уже построены два однонаправленных списка, элементами которых являются целые числа. Написать функцию, которая определяет, является ли данный список "перевертышем" другого списка.
3.32. Предположим, что уже построены и заданы указателями P1 и P2 однонаправленные списки, элементами которых являются целые числа. Написать программу, которая проверяет эти списки на равенство.
3.33. Многочлен P(x) = an*xn + an-1*xn-1+...+ ao с целыми коэффициентами представьте в виде списка, причем, если ai =0, то соответствующее звено в список не включается. Описать функцию Equal(p,q), проверяющую на равенство многочлены p и q.
Подсчет
3.34. Разработать функцию для подсчета количества элементов в заданном линейном списке.
3.35. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются целые числа. Написать программу, которая находит минимальное значение элементов списка P и номер первого элемента с этим значением.
3.36. Предположим, что уже построен и задан указателем P однонаправленный список, элементами которого являются вещественные числа. Написать программу, которая находит среднее арифметическое элементов списка P.
3.37. Предположим, что уже построен однонаправленный список, элементами которого являются целые числа. Написать программу, которая находит сумму последнего и предпоследнего элементов списка L.
3.38. Предположим, что уже построен однонаправленный список, элементами которого являются строки. Написать программу, подсчитывающую количество строк в списке L, которые начинаются и оканчиваются одним и тем же символом.
3.39. Предположим, что уже построен однонаправленный список, элементами которого являются строки. Написать программу, подсчитывающую количество строк в списке L, которые начинаются с того же символа, что и следующая строка.
3.40. Предположим, что уже построен однонаправленный список, элементами которого являются строки. Написать программу, подсчитывающую количество строк в списке L, которые совпадают со строкой, находящейся в последнем звене списка.
3.41*. Составить программу для лексического анализа текста. Она должна для данного текстового файла T найти все различные слова и указать количество их повторений, а также номер первой строки, в которой они встречаются.
Указание. Различные слова хранить в списке из записей следующего вида:
· слово длиной не более 15 символов;
· число повторений данного слова;
· указатель на номер строки;
· указатель на следующее слово.
3.42. Многочлен P(x) = an*xn + an-1*xn-1+...+ ao с целыми коэффициентами представьте в виде списка, причем, если ai=0, то соответствующее звено в список не включается. Опишите функцию Value(p,x), вычисляющую значение многочлена p в целочисленной точке x.
Раздел 4. Перегрузка операций
4.1. Перегрузить бинарную операцию “+” для матриц, используя дружественную функцию.
4.2. Перегрузить бинарную операцию “*” для матриц, используя метод класса.
4.3. Перегрузить бинарную операцию “-“ для матриц, используя глобальную функцию.
4.4. Перегрузить бинарную операцию “/“ для матриц, используя дружественную функцию.
4.5. Перегрузить операцию “++“ для матриц, реализовав префиксную и инфиксную формы, используя метод класса.
4.6. Перегрузить бинарную операцию “%=“ для матриц, используя глобальную функцию.
4.7. Перегрузить операцию “++“ для строк: код каждого символа строки должен увеличиться на 1 (в префиксной форме) и на 2 (в инфиксной форме), используя дружественную функцию.
4.8. Перегрузить бинарную операцию “+=“ для строк, используя метод класса: код каждого символа строки должен увеличиться на заданное в операции число.
4.9. Перегрузить бинарную операцию “%” для матриц, используя глобальную функцию: в результате должна получаться матрица, на соответствующих местах которой находятся остатки от деления соответствующих значений.
4.10. Перегрузить бинарную логическую операцию “&&“ для матриц, используя метод класса: в результате должна получаться матрица, на соответствующих местах которой находятся результаты выполнения этой операции над соответствующими элементами матрицы.
4.11. Перегрузить бинарную операцию “+” для строк, используя дружественную функцию: коды соответствующих символов складываются.
4.12. Перегрузить бинарную операцию “+” для строк, содержащих двоичные числа, используя глобальную функцию.
4.13. Перегрузить бинарную логическую операцию “==” для матриц, используя метод класса.
4.14. Перегрузить бинарную логическую операцию “>=” для матриц, используя метод класса. Одна матрица считается больше другой, если больше сумма всех ее элементов.
4.15. Перегрузить унарную логическую операцию “!” для матриц, используя дружественную функцию.
Раздел 5. Шаблоны функций
Реализовать программу, содержащую шаблон следующей функции.
5.1. Дано число a. Вычислить f(a), где f - периодическая функция с периодом 1.5, совпадающая на отрезке [0,1.5] с функцией x3 - 2.25x.
5.2. Дано число n. а) Сколько цифр в числе n? б) Найти знакочередующюся сумму цифр числа n (пусть запись n в десятичной системе есть abcd...; найти a-b+c-d...).
5.3. Даны число n и натуральное число m. Получить сумму m последних цифр числа n.
5.4. В матрице Z(l,l) каждый элемент столбца разделить на диагональный, стоящий в том же столбце.
5.5. Дана матрица A(k,l). Найти вектор B(l), каждый элемент которого равен сумме элементов соответствующего столбца матрицы А.
5.6. В матрице K(n,n) все элементы главной диагонали равны нулю. Присвоить каждому диагональному элементу разность между суммами элементов соответствующих строки и столбца.
5.7. Если в матрице P(m,n) есть отрицательные элементы, найти наибольший из них.
5.8. В массиве A(n) каждый элемент, кроме первого, заменить суммой всех предыдущих элементов исходного массива.
5.9. В массиве А(N) определить максимальное количество подряд идущих положительных элементов, не прерываемых ни нулями, ни отрицательными элементами.
5.10. Дана квадратная матрица порядка t. Для каждого столбца матрицы найти наибольший элемент. Вычислить и напечатать сумму найденных наибольших элементов.
5.11. Найти сумму элементов квадратной таблицы, лежащих ниже обеих диагоналей.
5.12. Даны два массива целых чисел А и В, упорядоченные по возрастанию. Поместить все элементы этих массивов в массив С, который также должен быть упорядочен по возрастанию.
5.13. Составить программу определения номера строки и столбца матрицы размером n*n, на пересечении которых находится наибольший элемент.
5.14. Написать программу, которая меняет значение каждого элемента двумерной таблицы на сумму окружающих его восьми членов, оставляя границу массива неизменной.
5.15. Написать программу, которая меняет местами значения элементов таблицы чисел А(N,N), симметричных относительно главной диагонали.
Распределение задач по вариантам
| Вариант 1: | 1.13; | 2.2; | 3.1; 3.28; | 4.1 | 5.1 |
| Вариант 2: | 1.15; | 2.3; | 3.2; 3.29; | 4.2 | 5.2 |
| Вариант 3: | 1.14; | 2.4; | 3.3; 3.30; | 4.3 | 5.3 |
| Вариант 4: | 1.12; | 2.5; | 3.4; 3.31; | 4.4 | 5.4 |
| Вариант 5: | 1.11; | 2.6; | 3.5; 3.32; | 4.5 | 5.6 |
| Вариант 6: | 1.10; | 2.7; | 3.6; 3.33; | 4.6 | 5.5 |
| Вариант 7: | 1.9; | 2.8; | 3.7; 3.34; | 4.7 | 5.8 |
| Вариант 8: | 1.8; | 2.9; | 3.8; 3.35; | 4.8 | 5.7 |
| Вариант 9: | 1.7; | 2.10; | 3.9; 3.36; | 4.9 | 5.10 |
| Вариант 10: | 1.6; | 2.11; | 3.10; 3.37; | 4.10 | 5.12 |
| Вариант 11: | 1.4; | 2.12; | 3.16; 3.38; | 4.11 | 5.9 |
| Вариант 12: | 1.3; | 2.13; | 3.17; 3.39; | 4.12 | 5.13 |
| Вариант 13: | 1.5; | 2.16; | 3.18; 3.40; | 4.13 | 5.12 |
| Вариант 14: | 1.2; | 2.15; | 3.14; 3.41; | 4.14 | 5.14 |
| Вариант 15: | 1.1; | 2.14; | 3.11; 3.42; | 4.15 | 5.15 |
|
|
|
