 |
Геометрические преобразования
|
|
|
|
Введение
Машинная графика — это сложная и многосторонняя дисциплина. Основное принципиальное требование к разработке систем машинной графики состоит в необходимости глубокого понимания связи ее практических аспектов со спецификой конкретного приложения. Фундаментом большинства приложений машинной графики являются математические методы, особенно геометрия и способы преобразования.
В настоящее время графика представляет собой важнейшую дисциплину для специалистов из многих областей знания, и в частности, для проектировщиков электронных устройств, инженеров, математиков, физиков и художников. Сегодня в совершенстве разработаны прежние концепции машинной графики, а также предложены новые идеи. Однако основополагающие математические понятия остались неизменными. Глубокое овладение базовыми математическими концепциями до сих пор остается главным ключом к пониманию и дальнейшему развитию машинной графики.
Поэтому для изучения ее необходимо разделить на более простые обозримые части, учитывая при этом, что конечным результатом машинной графики является изображение. Его, разумеется, можно использовать для самых различных целей: технического чертежа, деталировки в справочном руководстве, изображения архитектурной конструкции, как одного из возможных вариантов, так и эскиза проекта, рекламной иллюстрации либо отдельного кадра из мультфильма.
Основной целью данной курсовой работы является изучение математических и алгоритмических основ геометрического моделирования. Понять такие основы невозможно, просто ознакомившись с теоретическими сведениями по этой области. Поэтому задачей работы является именно практическая разработка “с нуля” трехмерной модели, в моем случае цилиндра с конусным отверстием.
|
|
|
Создание модели можно разбить на следующие основные этапы:
1. Расчет геометрии объекта
1.1 Выбор модели представления
1.2 Расчет вершин объекта
1.3 Построение полигонов объекта и нормалей к ним
2. Реализация механизмов перемещения и поворота объекта в пространстве
3. Реализация механизмов перемещения и поворота камеры в пространстве (проекции)
4. Реализация алгоритма удаления невидимых граней объекта
5. Моделирование освещения
Каждый этап можно разбить на ряд подзадач. Все задачи решаются исходя из специфики моделируемого объекта.
1. Описание объекта и получение геометрической модели
Целью курсового проекта является разработка приложения, позволяющего получать реалистичное изображения 3-х мерного объекта, представляющего собой полигональную сетку, его преобразование и его проецирование. Объект представляет собой трехмерную модель цилиндра с конусным отверстием. Язык исполняемого приложения – С#.
Исходные данные к проекту: Цилиндр + конусное отверстие (соосно).
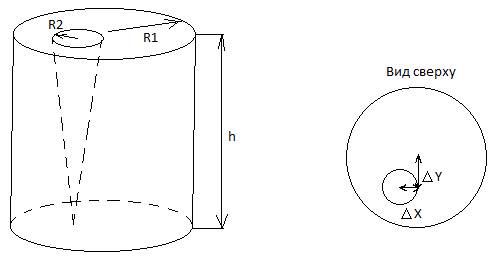
Рис. 1.1. Исходные данные 3-х мерного объекта
R1 - радиус цилиндра;
R2 - радиус основания конусного отверстия;
h - высота цилиндра и конусного отверстия;
∆x и ∆y - смещение центра конусного отверстия относительно центра цилиндра по x и у соответственно;
appr - степень аппроксимации (одинакова для цилиндра и конусного отверстия).
Объект представляет собой набор граней. Грань в свою очередь это набор рёбер, ребро - состоит их двух точек (начальная и конечная), точка описывается тремя координатами (х, у, z). Указав необходимые параметры (размеры) фигур, происходит расчёт координат вершин.

Рис.1.2 Значение параметров модели
В зависимости от значения аппроксимации, количество точек будет изменяться. С помощью геометрических формул получим X, Y и Z -координаты узлов для исходного положения объектов. За исходное положение примем нулевые смещения по всем осям и нулевые значения углов поворота объекта вокруг каждой из координатных осей.
|
|
|
for (int i = 0; i < 2 * appr; i++)
{
cylinderP[i].x = R1 * Math.Cos(angle * Math.PI / 180);
cylinderP[i].y = R1 * Math.Sin(angle * Math.PI / 180);
if (i < appr)
cylinderP[i].z = 0;
else
cylinderP[i].z = h;
angle += 360 / appr;//делим окружность на равные части
}
coneP[0].x = 0+dx;
coneP[0].y = 0+dy;
coneP[0].z = 0;
for (int i = 1; i < appr_cone + 1; i++)
{
coneP[i].x = R2 * Math.Cos(angle * Math.PI / 180) + dx;
coneP[i].y = R2 * Math.Sin(angle * Math.PI / 180) + dy;
coneP[i].z = h;
angle += 360 / appr_cone;
}
Объект разбивается на грани следующим образом. Боковые грани цилиндра будут состоять из 4х рёбер, нижнее основание (сплошное) - число ребер равно значению аппроксимации, а верхнее (с отверстием) - удвоенному значению аппроксимации. Боковые грани конусного отверстия будут состоять из 3х рёбер, а число рёбер основания будет равно значению аппроксимации.
Каждая грань задается своим цветом.

Рис. 1.3. Вид 3-х мерного объекта
Геометрические преобразования
Координаты хранятся неизменными, а для получения координат после пространственных преобразований для новых положений применяется умножение на матрицы преобразований.
Вращение
Преобразование может состоять из любых комбинаций вращения, перемещения и масштабирования. Матрица вращения или циклического сдвига позволяет вращать точку вокруг любой из осей координат. По оси X матрица вращения выглядит следующим образом:

RX[1, 1] = Math.Cos(int.Parse(povorot_RX.Value.ToString()) * Math.PI * 2 / 360);
RX[1, 2] = Math.Sin(int.Parse(povorot_RX.Value.ToString()) * Math.PI * 2 / 360);
RX[2, 1] = -Math.Sin(int.Parse(povorot_RX.Value.ToString()) * Math.PI * 2 / 360);
RX[2, 2] = Math.Cos(int.Parse(povorot_RX.Value.ToString()) * Math.PI * 2 / 360);
где Ө - угол вращения относительно оси Х.
Вращение вокруг оси Y:
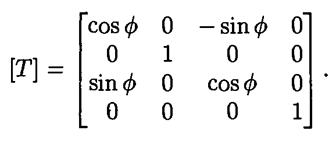
RY[0, 0] = Math.Cos(int.Parse(povorot_RY.Value.ToString()) * Math.PI * 2 / 360);
RY[0, 2] = -Math.Sin(int.Parse(povorot_RY.Value.ToString()) * Math.PI * 2 / 360);
RY[2, 0] = Math.Sin(int.Parse(povorot_RY.Value.ToString()) * Math.PI * 2 / 360);
RY[2, 2] = Math.Cos(int.Parse(povorot_RY.Value.ToString()) * Math.PI * 2 / 360);
где Фи - угол вращения относительно оси У.
Вращение вокруг оси Z:
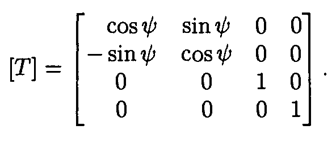
RZ[0, 0] = Math.Cos(int.Parse(povorot_RZ.Value.ToString()) * Math.PI * 2 / 360);
RZ[0, 1] = Math.Sin(int.Parse(povorot_RZ.Value.ToString()) * Math.PI * 2 / 360);
RZ[1, 0] = -Math.Sin(int.Parse(povorot_RZ.Value.ToString()) * Math.PI * 2 / 360);
RZ[1, 1] = Math.Cos(int.Parse(povorot_RZ.Value.ToString()) * Math.PI * 2 / 360);
где Пси - угол вращения относительно оси Z.
Перемещение
|
|
|
Матрица перемещения перемещает точку с координатами (x, y, z) в новую точку (x1, y1, z1). Данная матрица имеет вид:

T[3, 0] = int.Parse(perenos_dX.Value.ToString());
T[3, 1] = int.Parse(perenos_dY.Value.ToString());
T[3, 2] = int.Parse(perenos_dZ.Value.ToString());
где l – смещение объекта по оси X, m – смещение объекта по оси Y, n – смещение объекта по оси Z.
Масштабирование
Масштабирование объекта производится с помощью матрицы масштабирования. Sx - масштабирование относительно оси OX, Sy - масштабирование относительно OY, Sz - масштабирование относительно OZ.

S[0, 0] = int.Parse(mashtab_SX.Value.ToString());
S[1, 1] = int.Parse(mashtab_SY.Value.ToString());
S[2, 2] = int.Parse(mashtab_SZ.Value.ToString());
Как уже упоминалось ранее, в памяти мы постоянно храним только координаты объектов сцены для исходного состояния. При изменении положения тела мы рассчитываем новые координаты, исходя из текущих углов поворота и смещений. Поэтому кроме исходных координат также сохраняются суммарные повороты и смещения.
При изменении положения объекта, смещения и углы прибавляются к текущим. На основании полученных значений формируются все матрицы преобразований, после чего, путем перемножения этих матриц получаем общую матрицу преобразования для текущего положения и состояния сцены.
R = umnozhen(umnozhen(RX, RY), RZ);// получение результирующей матрицы для поворота
Q = umnozhen(umnozhen(T, S), R);// получение результирующей матрицы
Теперь мы можем получить координаты вершин объекта, произвольно расположенного в пространстве и с произвольным коэффициентом масштабирования, путем матричного перемножения вектора их координат на общую матрицу преобразования.
Проецирование
Описанные выше преобразования координат объекта трехмерны, т. е. являются преобразованиями одного трехмерного пространства в другое. Однако для наблюдения результатов на двумерной поверхности требуется проецирование из трехмерного пространства в двумерное. Результат этого проецирования называется плоской геометрической проекцией. Ниже изображена иерархия плоских геометрических проекций. 
Для получения координат объекта в какой-либо плоской проекции, кроме матрицы преобразования, необходимо исходные координаты вершин умножить на соответствующую матрицу проекции. Матрица проецирования из трехмерного пространства в двумерное всегда содержит столбец из нулей.
|
|
|
В данной работе реализованы четыре проекции: ортографическая, аксонометрическая, косоугольная и перспективная. Рассмотрим эти проекции более подробно.
Ортографическая проекция
Эта проекция является самой простой из параллельных проекций. Она используется обычно в инженерных чертежах. В этом случае точно изображается правильные или «истинные» размер и форма одной плоской грани объекта.
Ортографические проекции — это проекции на одну из координатных плоскостей x = 0, у = 0 или z = 0. Матрица проекции на плоскость z = 0 имеет вид




Рис. 3.1. Прямоугольные проекции
|
|
|


