Главная | Обратная связь | Поможем написать вашу работу!

Интерференция волн от двух когерентных источников

ИНТЕРФЕРЕНЦИЯ СВЕТА

Основные формулы

• Скорость света в среде

v = c/n,

где с — скорость света в вакууме; п — абсолютный показатель преломления среды.

• Оптическая длина пути световой волны

L=nl,

где l — геометрическая длина пути световой волны в среде с показателем преломления п.

3. Оптическая разность хода двух световых волн

Δ= L₁—L₂.

• Оптическая разность хода световых волн, отраженных от верхней и нижней поверхностей тонкой плоскопараллельной пластинки или пленки, находящейся в воздухе (рис. 30.1, а),

Δ= , или Δ= 2dn cos ε₂’ + λ/2, где d — толщина пластинки (пленки); ε₁— угол падения; ε₂’ -— угол преломления.

Второе слагаемое в этих формулах учитывает изменение оптической длины пути световой волны на λ/2 при отражении ее от среды оптически более плотной.

В проходящем свете (рис. 30.1, б) отражение световой волны происходит от среды оптически менее плотной и дополнительной разности хода световых лучей не возникает.

• Связь разности фаз Δφ колебаний с оптической разностью хода волн

Δφ=2 πΔ/λ..

• Условие максимумов интенсивности света при интерференции

Δ= ±kλ (k = 0,l,2, 3, …).

• Условие минимумов интенсивности света при интерференции

Δ= ± (2k+1) (λ/2).

• Радиусы светлых колец Ньютона в отраженном свете (или темных в проходящем)

r_k = .

где k — номер кольца (k =1, 2, 3, …); R — радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.

Радиусы темных колец в отраженном свете (или светлых в проходящем)

Примеры решения задач

Пример 1. В точку А экрана от источника S₁ монохроматического света длиной волны λ =0,5мкм приходят два луча: непосредственно от источника луч S₁A, перпендикулярный экрану, и луч S₁BA, отраженный в точке В от зеркала, параллельного лучу S₁A (рис. 30.2). Расстояние l₁ экрана от источника равно 1 м, расстояние h от луча S₁A до плоскости зеркала равно 2 мм. Определить: 1) что будет наблюдаться в точке А экрана — усиление или ослабление интенсивности; 2) как изменится интенсивность в точке А, если на пути луча S₁A перпендикулярно ему поместить плоскопараллельную пластинку стекла (n =1,55) толщиной d =6 мкм.

Решение. Построим мнимое изображение S₂ источника S₁ в зеркале (рис. 30.3). Источники S₁ и S₂ являются когерентными, поэтому при сложении волн, приходящих от этих источников на экран, возникает интерференционная картина. Усиление или ослабление интенсивности в той или иной точке экрана зависит от оптической разности хода Δ интерферирующих лучей, другими словами, от числа т полуволн, укладывающихся на оптической разности хода:

(1)

Если т — целое четное, то интенсивность будет максимальной; если т — целое нечетное, то интенсивность минимальна. При дробном т происходит или частичное усиление (если т ближе к четному числу), или частичное ослабление (если т ближе к нечетному числу).

1. Оптическая разность хода Δ₁ будет складываться из геометрической разности l₂ — l₁ (оба луча идут в воздухе) и дополнительной разности хода λ/2, обусловленной изменением фазы колебаний на π при отражении от среды оптически более плотной. Таким образом,

Δ₁= l₂—l₁+ λ/2. (2)

Так как l₂ = (рис. 30.3), то

l₂—l₁ = .

Величина H/l₁<<1, поэтому для вычисления корня можно воспользоваться приближенной формулой (см. табл. 3)

при а <<1. Применив ее, получим

Подставив полученное выражение l₂—l₁ в формулу (2), найдем

. Зная Δ₁, по формуле (1) найдем m₁:

Так как Н = 2h, то окончательно получим

После вычисления найдем

m₁ =33.

Так как на разности хода укладывается нечетное число длин полуволн, то в точке А наблюдается минимум интенсивности.

2. Стеклянная пластина толщиной d, поставленная на пути луча S₁A (рис. 30.3), изменит оптическую длину пути. Теперь оптическая длина пути L будет складываться из геометрической длины пути l₁—d и оптической длины пути nd луча в самой пластине, т. е.

L= (l₁—d)+nd==l₁+ (n— 1 )d.

Оптическая разность хода лучей

Δ₂= l₂—L+λ/2 = l₂— [ l₁+ (n— l )d ] +λ/2, или

Δ₂= Δ₁—(n —1) d.

Пользуясь формулой (1), найдем

Произведя вычисления, получим m₂ =19,8.

Число длин полуволн оказалось дробным. Так как 19,8 ближе к целому четному числу 20, чем к целому нечетному числу 19, то в точке А будет частичное усиление.

Пример 2. На толстую стеклянную пластинку, покрытую очень тонкой пленкой, показатель преломления n₂ вещества которой равен 1,4, падает нормально параллельный пучок монохроматического света (λ=0,6 мкм). Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину d пленки.

Решение. Из световой волны, падающей на пленку, выделим узкий пучок SA. Ход этого пучка в случае, когда угол падения ε₁ 0, показан на рис. 30.4. В точках A и В падающий пучок частично отражается и частично преломляется. Отраженные пучки света AS₁ и BCS₁ падают на собирающую линзу L, пересекаются в ее фокусе F и интерферируют между собой.

Так как показатель преломления воздуха (n₁= 1,00029) меньше показателя преломления вещества пленки (n₂ =1,4), который, в свою очередь, меньше показателя преломления стекла (n₃ =1,5), то в обоих случаях отражение происходит от среды оптически более плотной, чем та среда, в которой идет падающая волна. Поэтому фаза колебания пучка света AS₁ при отражении в точке A изменяется на π рад и точно так же на π рад изменяется фаза колебаний пучка света BCS₂ при отражении в точке В. Следовательно, результат интерференции этих пучков света при пересечении в фокусе F линзы будет такой же, как если бы никакого изменения фазы колебаний ни у того, ни у другого пучка не было.

Как известно, условие максимального ослабления света при интерференции в тонких пленках состоит в том, что оптическая разность хода Δ интерферирующих волн должна быть равна нечетному числу полуволн; Δ=(2 k +1)(λ /2).

Как видно из рис. 30.4, оптическая разность хода

Δ= l₂n₂— l₁n₁ =(| АВ | +| ВС |) п₂—|AD | n₁.

Следовательно, условие минимума интенсивность света примет вид

(| АВ | +| ВС |) п₂—|AD | n₁ =(2 k +1)(λ /2).

Если угол падения ε₁ будет уменьшаться, стремясь к нулю, то AD 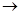0 и (| АВ|+|ВС| 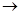2d, где d— толщина пленки. В пределе при ε₁=0 будем иметь

Δ=2 dn₂ =(2 k +1)(λ /2),

откуда искомая толщина пленки

Полагая k =0,1,2,3,…, получим ряд возможных значений толщины пленки:

и т.д.

Пример 3. На стеклянный клин нормально к его грани падает монохроматический свет с длиной волны λ =0,6 мкм. В возникшей при этом интерференционной картине на отрезке длиной l =1 см наблюдается 10 полос. Определить преломляющий угол θ клина.

Решение. Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти пучки когерентны, и поэтому наблюдается устойчивая картина интерференции. Так как интерференционные полосы наблюдаются при малых углах клина, то отраженные пучки света 1 и 2 (рис. 30.5) будут практически параллельны.

Темные полосы видны на тех участках клина, для которых разность хода кратна нечетному числу половины длины волны;

Δ=(2k+1) (λ/2), где k =0,1,2,…. (1)

Разность хода Δ двух волн складывается из разности оптических длин путей этих волн (2dn cosε₂’) и половины длины волны (λ/2).

Величина λ/2 представляет собой добавочную разность хода, возникающую при отражении волны от оптически более плотной среды. Подставляя в формулу (1) значение разности хода Δ, получим

2d_kn cos ε ₂’ + λ/2 = (2k + 1) (λ/2), (2)

где п — коэффициент преломления стекла (n =l,5); d_k— толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k; ε₂’—угол преломления.

Согласно условию, угол падения равен нулю, следовательно, и угол преломления ε₂’ равен нулю, a cos ε₂’ =1. Раскрыв скобки в правой части равенства (2), после упрощения получим

2d_kn = kλ (3)

Пусть произвольной темной полосе номера k соответствует определенная толщина клина в этом месте d_k а темной полосе номера k+10 соответствует толщина клина d_k₊₁₀. Согласно условию задачи, 10 полос укладываются на отрезке длиной l =1 см. Тогда искомый угол (рис. 30.5) будет равен

θ=(d_k+10 – d_k)/ l, (4)

где из-за малости преломляющего угла sin θ = θ (угол θ выражен в радианах).

Вычислив d_k и d_k+10 из формулы (3), подставив их в формулу (4) и произведя преобразования, найдем

θ=5 λ/(nl).

После вычисления получим

θ=2*10^-4paд.

Выразим θ в градусах. Для этого воспользуемся соотношением между радианом и секундой (см. табл. 6); 1 рад=2,06"*10⁵, т. е.

θ=2*10^-4*2,06''*10⁵=41,2'',

или в соответствии с общим правилом перевода из радиан в градусы

θ_град = θ_рад, θ = .

Искомый угол равен 41,2".

Задачи

Интерференция волн от двух когерентных источников

30.1. Сколько длин волн монохроматического света с частотой колебаний υ =5*10¹⁴ Гц уложится на пути длиной l =1,2 мм: 1) в вакууме; 2) в стекле?

30.2. Определить длину l₁ отрезка, на котором укладывается столько же длин волн в вакууме, сколько их укладывается на отрезке l₂ =3 мм в воде.

30.3. Какой длины l₁ путь пройдет фронт волны монохроматического света в вакууме за то же время, за какое он проходит путь длиной l₂ =1 м в воде?

30.4. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной h =1 мм. На сколько изменится оптическая длина пути, если волна падает на пластинку: 1) нормально; 2) под углом ε=30°?

30.5. На пути монохроматического света с длиной волны λ =0,6 мкм находится плоскопараллельная стеклянная пластина толщиной d =0,l мм. Свет падает на пластину нормально. На какой угол φ следует повернуть пластину, чтобы оптическая длина пути L изменилась на λ /2?

30.6. Два параллельных пучка световых волн I и II падают на стеклянную призму с преломляющим углом θ=30° и после преломления выходят из нее (рис. 30.6). Найти оптическую разность хода Δ световых волн после преломления их призмой.

30.7. Оптическая разность хода Δ двух интерферирующих волн монохроматического света равна 0,3λ. Определить разность фаз Δφ.

30.8. Найти все длины волн видимого света (от 0,76 до 0,38 мкм), которые будут: 1) максимально усилены; 2) максимально ослаблены при оптической разности хода Δ интерферирующих волн, равной 1,8 мкм.

30.9. Расстояние d между двумя когерентными источниками света (λ=0,5 мкм) равно 0,1 мм. Расстояние b между интерференционными полосами на экране в средней части интерференционной картины равно 1 см. Определить расстояние l от источников до экрана.

30,10. Расстояние d между двумя щелями в опыте Юнга равно 1мм, расстояние l от щелей до экрана равно 3 м. Определить длину

волны λ, испускаемой источником монохроматического света, если ширина b полос интерференции на экране равна 1,5 мм.

30.11. В опыте Юнга расстояние d между щелями равно 0,8 мм. На каком расстоянии l от щелей следует расположить экран, чтобы ширина b интерференционной полосы оказалась равной 2 мм?

30.12. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние l от них до экрана равно 3 м. Длина волны λ=0,6 мкм. Определить ширину b полос интерференции на экране.

30.13. Источник S света (λ=0,6 мкм) и плоское зеркало М расположены, как показано на рис. 30.7 (зеркало Ллойда). Что будет наблюдаться в точке Р экрана, где сходятся лучи SP и SMP,— свет или темнота, если | SP|=r=2 м, a =0,55 мм, | SM| =| MP|?

Интерференция света в тонких пленках

30.14. При некотором расположении зеркала Ллойда ширина b интерференционной полосы на экране оказалась равной 1 мм. После того как зеркало сместили параллельно самому себе на расстояние Δ d =0,3 мм, ширина интерференционной полосы изменилась. В каком направлении и на какое расстояние Δ l следует переместить экран, чтобы ширина интерференционной полосы осталась прежней? Длина волны λ монохроматического света равна 0,6 мкм.

30.15. Плоскопараллельная стеклянная пластинка толщиной d =1,2 мкм и показателем преломления n =1,5 помещена между двумя средами с показателями преломления n₁ и n₂ (рис. 30.8). Свет с длиной волны λ=0,6 мкм падает нормально на пластинку. Определить оптическую разность хода Δ волн 1 и 2, отраженных от верхней и нижней поверхностей пластинки, и указать, усиление или ослабление интенсивности света происходит при интерференции в следующих случаях: 1) n₁<.п<n₂; 2) n₁>n>n₂; 3) п₁<п>п₂; 4) n₁>n<n₂.

30.16. На мыльную пленку (n =1,3), находящуюся в воздухе, падает нормально пучок лучей белого света. При какой наименьшей толщине d пленки отраженный свет с длиной волны λ=0,55 мкм окажется максимально усиленным в результате интерференции?

30.17. Пучок монохроматических (λ=0,6 мкм) световых волн падает под углом ε₁=30° на находящуюся в воздухе мыльную пленку (n =1,3). При какой наименьшей толщине d пленки отраженные световые волны будут максимально ослаблены интерференцией? максимально усилены?

30.18. На тонкий стеклянный клин (n =1,55) падает нормально монохроматический свет. Двугранный угол α между поверхностями клина равен 2'. Определить длину световой волны λ, если расстояние b между смежными интерференционными максимумами в отраженном свете равно 0,3 мм.

30.19. Поверхности стеклянного клина образуют между собой угол θ=0,2'. На клин нормально к его поверхности падает пучок лучей монохроматического света с длиной волны λ=0,55 мкм. Определить ширину b интерференционной полосы.

30.20. На тонкий стеклянный клин в направлении нормали к его поверхности падает монохроматический свет (λ=600 нм). Определить угол θ между поверхностями клина, если расстояние b между смежными интерференционными минимумами в отраженном свете равно 4 мм.

30.21. Между двумя плоскопараллельными стеклянными пластинками положили очень тонкую проволочку, расположенную параллельно линии соприкосновения пластинок и находящуюся на расстоянии l =75 мм от нее. В отраженном свете (λ=0,5 мкм) на верхней пластинке видны интерференционные полосы. Определить диаметр d поперечного сечения проволочки, если на протяжении а =30 мм насчитывается m =16 светлых полос.

30.22. Две плоскопараллельные стеклянные пластинки приложены одна к другой так, что между ними образовался воздушный клин с углом θ, равным 30". На одну из пластинок падает нормально монохроматический свет (λ=0,6 мкм). На каких расстояниях l₁ и l₂ от линии соприкосновения пластинок будут наблюдаться в отраженном свете первая и вторая светлые полосы (интерференционные максимумы)?

30.23. Две плоскопараллельные стеклянные пластинки образуют клин с углом θ=30'. Пространство между пластинками заполнено глицерином. На клин нормально к его поверхности падает пучок монохроматического света с длиной волны λ=500 нм. В отраженном свете наблюдается интерференционная картина. Какое число N темных интерференционных полос приходится на 1 см длины клина?

30.24. Расстояние Δ r_2,1 между вторым и первым темным кольцами Ньютона в отраженном свете равно 1 мм. Определить расстояние Δ r_10,9 между десятым и девятым кольцами.

30.25. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Определить толщину d слоя воздуха там, где в отраженном свете (λ=0,6 мкм) видно первое светлое кольцо Ньютона.

30.26. Диаметр d₂ второго светлого кольца Ньютона при наблюдении в отраженном свете (λ=0,6 мкм) равен 1,2 мм. Определить оптическую силу D плосковыпуклой линзы, взятой для опыта.

30.27. Плосковыпуклая линза с оптической силой Ф=2 дптр выпуклой стороной лежит на стеклянной пластинке. Радиус r, четвертого темного кольца Ньютона в проходящем свете равен 0,7 мм. Определить длину световой волны.

30.28. Диаметры d_i и d_k двух светлых колец Ньютона соответственно равны 4,0 и 4,8 мм. Порядковые номера колец не определялись, но известно, что между двумя измеренными кольцами расположено три светлых кольца. Кольца наблюдались в отраженном свете (λ=500 нм). Найти радиус кривизны плосковыпуклой линзы, взятой для опыта.

30.29. Между стеклянной пластинкой и лежащей на ней плосковыпуклой стеклянной линзой налита жидкость, показатель преломления которой меньше показателя преломления стекла. Радиус r₈ восьмого темного кольца Ньютона при наблюдении в отраженном свете (λ=700 нм) равен 2 мм. Радиус R кривизны выпуклой поверхности линзы равен 1 м. Найти показатель преломления n жидкости.

30.30. На установке для наблюдения колец Ньютона был измерен в отраженном свете радиус третьего темного кольца (k =3). Когда пространство между плоскопараллельной пластиной и линзой заполнили жидкостью, то тот же радиус стало иметь кольцо с номером, на единицу большим. Определить показатель преломления п жидкости.

30.31. В установке для наблюдения колец Ньютона свет с длиной волны λ=0,5мкм падает нормально на плосковыпуклую линзу с радиусом кривизны R₁ =1 м, положенную выпуклой стороной на вогнутую поверхность плосковогнутой линзы с радиусом кривизны R₂ =2 м. Определить радиус r₃ третьего темного кольца Ньютона, наблюдаемого в отраженном свете.

30.32. Кольца Ньютона наблюдаются с помощью двух одинаковых плосковыпуклых линз радиусом R кривизны равным 1м, сложенных вплотную выпуклыми поверхностями (плоские поверхности линз параллельны). Определить радиус r₂ второго светлого кольца, наблюдаемого в отраженном свете (λ=660 нм) при нормальном падении света на поверхность верхней линзы.

Интерференционные приборы

30.33. На экране наблюдается интерференционная картина от двух когерентных источников света с длиной волны λ=480 нм. Когда на пути одного из пучков поместили тонкую пластинку из плавленого кварца с показателем преломления n =1,46, то интерференционная картина сместилась на m =69 полос. Определить толщину d кварцевой пластинки.

30.34. В оба пучка света интерферометра Жамена были помещены цилиндрические трубки длиной l =10 см, закрытые с обоих концов плоскопараллельными прозрачными пластинками; воздух из трубок был откачан. При этом наблюдалась интерференционная картина в виде светлых и темных полос. В одну из трубок был впущен водород, после чего интерференционная картина сместилась на m =23,7 полосы. Найти показатель преломления п водорода. Длина волны λ света равна 590 нм.

30.35. В интерферометре Жамена две одинаковые трубки длиной l =15 см были заполнены воздухом. Показатель преломления n₁ воздуха равен 1,000292. Когда в одной из трубок воздух заменили ацетиленом, то интерференционная картина сместилась на m =80 полос. Определить показатель преломления n₂ ацетилена, если в интерферометре использовался источник монохроматического света с длиной волны λ=0,590 мкм.

30.36. Определить перемещение зеркала в интерферометре Майкельсона, если интерференционная картина сместилась на т =100 полос. Опыт проводился со светом с длиной волны λ=546 нм.

30.37. Для измерения показателя преломления аргона в одно из плеч интерферометра Майкельсона поместили пустую стеклянную трубку длиной l =12 см с плоскопараллельными торцовыми поверхностями. При заполнении трубки аргоном (при нормальные условиях) интерференционная картина сместилась на m =106 полос. Определить показатель преломления п аргона, если длина волны λ света равна 639 нм.

30.38. В интерферометре Майкельсона на пути одного из интерферирующих пучков света (λ=590 нм) поместили закрытую с обеих сторон стеклянную трубку длиной l =10 см, откачанную до высокого вакуума. При заполнении трубки хлористым водородом произошло смещение интерференционной картины. Когда хлористый водород был заменен бромистым водородом, смещение интерференционной картины возросло на Δ m =42 полосы. Определить разность Δ n показателей преломления бромистого и хлористого водорода.

Поделиться:

Воспользуйтесь поиском по сайту: