Способы получения когерентных источников

Работа № 2. ИНТЕРФЕРЕНЦИЯ СВЕТА

Цель работы: получение интерференционной картины разными способами, определение длины волны по интерференционной картине.

Вопросы, знание которых обязательно

для допуска к выполнению работы:

1. В чем заключается явление интерференции?

2. Какие источники называются когерентными?

3. Способы получения когерентных источников, методом деления волнового фронта.

4. Способы получения когерентных источников, методом деления амплитуд.

5. Условия наблюдения интерференционной картины.

6. Оптическая разность хода

7. Условия максимума и минимума интерференционной картины

ВВЕДЕНИЕ

При наложении световых волн происходит перераспределение светового потока в пространстве, в результате чего наблюдается явление интерференции, заключающееся в том, что в одних местах происходит усиление света, в других – ослабление. Если две световые волны придут в одну точку пространства в одинаковой фазе, они будут усиливать друг друга. В этой точке образуется светлый участок интерференционной картины. В тех же точках пространства, в которые волны приходят в противоположных фазах, они будут ослаблять друг друга и там будет темный участок.

Таким образом, результат интерференции зависит от разности фаз интерферирующих волн. Чтобы картина интерференции в каждой точке пространства не менялась со временем, необходимо, чтобы разность фаз была постоянной. В противном случае в каждой точке пространства волны будут то усиливать, то ослаблять друг друга, а глаз, воспринимая усредненную картину, не обнаружит интерференционных полос. Следовательно, наблюдать интерференционную картину можно лишь в том случае, если интерферирующие волны имеют строго одинаковую частоту и постоянную разность фаз в пространстве и во времени.

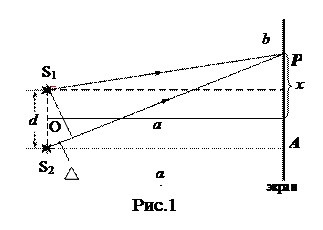Источники света, излучающие волны одинаковой частоты и с постоянной разностью фаз, называются когерентными.Для образования картины интерференции необходимо, чтобы пучки электромагнитных волн при своем движении набрали разность хода. Рассмотрим интерференцию света от двух точечных когерентных источников S ₁ и S ₂, расстояние между которыми равно d (рис.1).

Проведем перпендикулярно отрезку S ₁ S ₂ через его середину прямую OA. Возьмем точку P на прямой параллельной S ₁ S ₂, и обозначим OA через а, а АР – через х.

Тогда по теореме Пифагора:

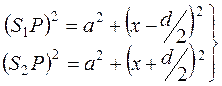, (1)

где и – пути, которые пройдут лучи света от источников S ₁ и S ₂ до точки P, в которой наблюдается интерференция. Из уравнений (1) следует, что оптическая разность хода между двумя лучами

. (2)

Тогда

, (3)

Если х и d малы по сравнению с а, то приближенно и

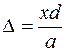. (4)

Если величина D равна нечетному числу полуволн, то световые волны придут в точку P в противофазе и погасят друг друга, интенсивность в этой точке будет минимальной: , где; k = 0,1,2…; λ – длина волны.

Если же равна четному числу полуволн, то световые волны придут в точку P в одинаковых фазах и усилят друг друга – интенсивность будет максимальной: , где ; λ – длина волны.

Таким образом, в точках будут светлые участки интерференционной картины, а в точках – темные участки интерференционной картины. В результате в плоскости РА будут наблюдаться светлые и темные полосы. Расстояние b между центрами соседних k -й и (k + 1 ) -й светлых полос составит:

. (5)

Такое же расстояние будет и между центрами темных полос.

Способы получения когерентных источников

Найти два точечных когерентных источника практически невозможно. Значительно проще поделить волновой фронт или амплитуду излученной волны. Наиболее распространенными методами получения когерентных источников являются: опыт Юнга, бипризма Френеля, билинза Бийе, «кольца» Ньютона, опыт Поля (с помощью плоскопараллельной пластины).

1. Бипризма Френеля (рис.2) состоит из двух остроугольных призм (с малыми преломляющими углами), сложенных основаниями. Обычно обе призмы имеют очень малые преломляющие углы B и C. В сечении бипризма Френеля представляет собой два равнобедренных треугольника с углом A, близким к 180º, тогда угол при вершине очень мал.

Свет от монохроматического источника S (например, от узкой освещенной щели, перпендикулярной плоскости чертежа) падает на бипризму и преломляется в ней. Угол падения лучей на бипризму мал, вследствие чего все лучи отклоняются бипризмой на одинаковый угол. В результате образуются две когерентные волны, исходящие из мнимых источников S₁ и S₂. В заштрихованной области за бипризмой преломленные пучки интерферируют, в результате чего образуется интерференционная картина, состоящая из светлых и темных полос.

2. Воздушный клин (кольца Ньютона). «Кольца Ньютона» представляют собой один из видов интерференции в тонкой пленке, а именно, полосы равной толщины в виде окружностей. Они получаются при наложении линзы радиуса R выпуклой поверхностью на отражающую стеклянную поверхность меньшей кривизны (например, плоскую). Вблизи места соприкосновения получается слой воздуха, толщина которого сравнима с длиной световой волны. Интерференция возникает в результате наложения лучей 1 и 2, после отражения от пластины и линзы (1¢ и 2¢) (рис.4). Полная разность хода между «усиливающими» друг друга лучами 1 и 2 определяется как ∆» 2d∙λ/2 (величина разности хода увеличена на λ /2вследствие потери полуволны лучом 2 при отражении от оптически более плотной поверхности на границе раздела воздух – стекло). Толщина воздушного зазора d зависит (рис.4) от расстояния r до точки соприкосновения линзы с пластинкой. Из треугольника АОС (рис. 4) имеем при R >> d. Для точек, в которых выполняется условие , будет наблюдаться максимум интенсивности. Отсюда радиус k - того светлого кольца . Аналогично радиус темного кольца .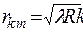

На практике кольца Ньютона наблюдают либо невооруженным глазом, помещая его на пути лучей 1 и 2 (рис.4), либо в фокальной плоскости окуляра микроскопа при использовании микроскопа. В отраженном свете в центре интерференционной картины наблюдается темное пятно, которое объясняется тем, что геометрическая разность хода между лучами 1 и 2 в области точки С равна нулю, а полуволна теряется при отражении от оптически более плотной поверхности на границе воздух – стекло.

Измеряя радиусы колец и зная длину волны λ, можно было бы найти по вышеприведенным формулам радиус кривизны линзы и обратно – по известному радиусу кривизны найти длину волны. Однако эти формулы неприменимы для опытной проверки. На поверхности даже очищенного стекла всегда присутствуют пылинки, и линза не примыкает плотно к плоскопараллельной пластинке, между ними имеется незначительный зазор величиной h. Вследствие зазора возникает дополнительная разность хода в 2 h. Тогда условие образования темных колец примет вид или , а радиус k -того темного кольца . На опыте измеряют радиусы темных колец r_k и строят зависимость r ² _kт (k), где k = 2, 3.... и использую следующее соотношение

, (13)

при известной величине λ находят R (или, наоборот, при известном R определяется λ).

В случае, если рассматриваем «кольца» Ньютона в проходящем свете, тогда не будет дополнительной разности хода в 2 h и, следовательно, там где в отраженном свете наблюдались темные кольца в походящем будут белыми и наоборот.

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: