 |
Анализ тенденция развития, колеблемости и цикличности рынка
|
|
|
|
Центральным моментом оценки и анализа рыночной конъюнктуры является изучение тенденций и особенностей его развития, его устойчивости. Для определения вектора и скорости его развития строятся динамические ряды показателей-индикаторов рынка и показателей деловой активности. Исчисляются базисные, цепные и средние за период темпы роста. Целесообразно также рассчитывать компаративные темпы роста для взаимообусловленных показателей, особенно в тех случаях, когда один показатель изменяется быстрее или медленнее другого.
Анализ основной тенденции развития
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Для обнаружения основной тенденции развития могут использоваться следующие основные методы:
укрупнение интервала динамического ряда;
метод скользящей средней;
аналитическое выравнивание ряда динамики.
Рассмотрим эти методы более подробно.
Укрупнение интервала динамического ряда
Смысл приема заключается в переходе от менее крупных интервалов к более крупным: от месячных - к квартальным, от квартальных - к годовым и т.д. Уровни укрупненных рядов вычисляются путем суммирования уровней за периоды, вошедшие в новый интервал, или путем вычисления среднего уровня по укрупненному интервалу. Пример выравнивания ряда путем укрупнения интервалов приведен в табл.2. Из нее следует, что при анализе месячной динамики объема продаж не ясна основная тенденция развития, а при переходе к более крупным интервалам она становится очевидной.
Таблица 2. Динамика объема продаж холодильников в 1997 году (тыс.шт.)
| Месяцы | 1 | 2 | 3
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||||
| Объем продаж в месяц | 2,3 | 2,4 | 2,2 | 2,1 | 3,2 | 2,9 | 2,8 | 3,0 | 3,0 | 2,8 | 3,2 | 3,3 | |||||
| Объем продаж в квартал | 6,9 | 8,2 | 8,8 | 9,3 | |||||||||||||
| Средний объем продаж в квартал | 2,3 | 2,73 | 2,93 | 3,1 | |||||||||||||
Метод скользящей средней
Для определения скользящей средней формируем укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получаем, постепенно сдвигаясь от начального уровня динамического ряда на один уровень. Тогда первый интервал будет включать уровни y1, y2,.... ym; второй - уровни y2, y3,.... ym+1 и т.д. Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяется сумма значений уровней, на основании которых рассчитываются скользящие средние. Полученная средняя относится к середине укрупненного интервала. В случае наличия четного числа уровней необходима дополнительная процедура центрирования. Скользящие средние можно рассчитывать по укрупненным интервалам разной продолжительности. Размер интервала необходимо выбирать таким образом, чтобы получить наглядную тенденцию развития процесса.
Пример расчета приведен в табл.3.
Когда скользящая средняя рассчитывается по четному числу уровней, необходимо провести дополнительное центрирование средней. Первая скользящая средняя относится не к конкретному уровню, а попадает в промежуток между двумя средними уровнями выравнивания (если выравнивание проводится по 6 месячным интервалам, то первая скользящая попадет в промежуток между 3 и 4 уровнем). Для отнесения скользящей средней к определенному уровню находится средняя из двух смежных скользящих средних, т.е. производится центрирование средних (см. табл.3).
Таблица 3. Динамика выпуска продукции предприятия в 1991-1995 гг.
| Год | Квартал | Фактический объем выпуска продукции, тыс. р. | Скользящая за четыре квартала, тыс. р. | Центрированная скользящая средняя, тыс. р. |
| 1 | 16 | - | - | |
| 1991 | 2 | 21 | 16,00 | - |
| . | 3 | 9 | 15,75 | 15,875 |
| . | 4 | 18 | 15,70 | 15,625 |
| . | 1 | 15 | 15,75 | 15,625 |
| 1992 | 2 | 20 | 15,75 | 15,750 |
| . | 3 | 10 | 16,25 | 16,000 |
| . | 4 | 18 | 17,25 | 16,750 |
| . | 1 | 17 | 18,00 | 17,625 |
| 1993 | 2 | 24 | 19,00 | 18,500 |
| . | 3 | 13 | 19,00 | 19,000 |
| . | 4 | 22 | 19,25 | 19,125 |
| . | 1 | 17 | 18,75 | 19,000 |
| 1994 | 2 | 25 | 18,50 | 18,625 |
| . | 3 | 11 | - | - |
| . | 4 | 21 | - | - |
Изучение основной тенденции развития методами укрупнения интервалов и скользящей средней является эмпирическим приемом предварительного анализа. Для того чтобы представить количественную модель, выражающую общую тенденцию развития динамического ряда, используют аналитическое выравнивание ряда динамики.
|
|
|

Аналитическое выравнивание ряда динамики
Основным содержанием метода аналитического выравнивания рядов динамики является расчет общей тенденции развития как функции времени:
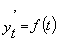 , ,
|
где
 - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
- уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней
 производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает основную тенденцию развития ряда динамики.
производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает основную тенденцию развития ряда динамики.
Простейшими моделями (формулами), выражающими тенденцию развития, являются следующие:
линейная функция - прямая
 ; ;
|
показательная функция
 ; ;
|
степенная функция - кривая второго порядка (парабола)
 . .
|
Расчет параметров функции обычно производится методом наименьших квадратов (МНК), в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическим и эмпирическим уровнями:
 , ,
|
где
 - выровненные (расчетные) уровни;
- выровненные (расчетные) уровни;
 - фактические уровни.
- фактические уровни.
Параметры уравнения
 , удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни.
, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни.
Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней).
Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. цепные коэффициенты роста практически постоянны.
|
|
|
Выравнивание по степенной функции (параболе второго порядка) используется в случае, если ряды динамики изменяются с постоянными цепными темпами прироста.
Нормальные уравнения МНК имеют вид:
для линейного тренда:
 , ,
 ; ;
|
для параболы второго порядка:
 , ,
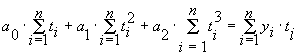 , ,
 , ,
|
где
 - уровни исходного ряда динамики;
- уровни исходного ряда динамики;
 - номера периодов или моментов времени (1,2,3:n);
- номера периодов или моментов времени (1,2,3:n);
n - число уровней ряда;
а0, а1, а2 - константы уравнений.
Для решения систем уравнений обычно применяется способ определителей или способ отсчета от условного начала.
Для упрощения расчетов удобнее воспользоваться способом отсчета от условного начала. При этом сумма показателей времени изучаемого ряда динамики должна быть равна нулю:
 . .
|
При нечетном числе уровней ряда динамики уровень, находящийся в середине ряда, принимается за условное начало отсчета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие выше этого уровня, обозначаются натуральными числами со знаком минус (-1, -2, -3 и т.д.), а ниже - натуральными числами со знаком плюс (+1, +2, +3 и т.д.).
Если число уровней динамического ряда четное, периоды времени верхней половины ряда (до середины) нумеруются -1, -2,
-3 и т.д., а нижней - +1, +2, +3 и т.д.. При этом условие (8) будет равно нулю и системы нормальных уравнений (6) и (7) преобразуются следующим образом:
для линейного тренда:
 , ,
 ; ;
|
для параболы второго порядка:
 , ,
 , ,
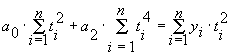 . .
|
По вычисленным параметрам производятся синтезирование трендовой модели функции, то есть полученных значений а0, а1, а2, и их подстановка в искомое уравнение.
Правильность расчетов аналитических уровней можно проверить по следующему условию - сумма значений эмпирического ряда должна совпадать с суммой вычисленных уровней выровненного ряда. При этом может возникнуть небольшая погрешность в расчетах из-за округлений вычисляемых величин.
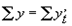 . .
|
Для анализа адекватности полученной зависимости используются различные критерии. Один из них - стандартизированная ошибка аппроксимации -
|
|
|
 :
:
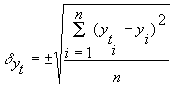 , ,
|
где
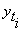 - теоретические уровни;
- теоретические уровни;
 - экспериментальные уровни;
- экспериментальные уровни;
n - число уровней ряда.
За наиболее адекватную принимается та функция (модель), у которой
 минимальная.
минимальная.
После выбора наиболее адекватной модели можно сделать прогноз на любой из периодов. При составлении прогнозов оперируют не точечной, а интервальной оценкой, определяя так называемые доверительные интервалы прогноза. Величина доверительного интервала определяется в общем виде следующим образом:
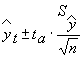 , ,
|
где
 - среднее квадратическое отклонение от тренда;
- среднее квадратическое отклонение от тренда;
 - табличное значение t-критерия Стьюдента при уровне значимости .Зависит от уровня значимости (%) и числа степеней свободы k=n-m.
- табличное значение t-критерия Стьюдента при уровне значимости .Зависит от уровня значимости (%) и числа степеней свободы k=n-m.
Величина
 определяется по формуле
определяется по формуле
 , ,
|
где yi и
 - соответственно фактические и расчетные значения уровней динамического ряда;
- соответственно фактические и расчетные значения уровней динамического ряда;
n - число уровней ряда;
m - количество параметров в уравнении тренда (для уравнения прямой m=2, для уравнения параболы 2-го порядка m=3).
После проведения необходимых расчетов определяется интервал, в котором с определенной вероятностью будет находиться прогнозируемая величина.
|
|
|


