Принцип включения и исключения

1.1. Вывод формулы. Пусть имеем N объектов и некоторый набор свойств а₁, …, а_n, которыми могут обладать эти объекты. Обозначим N(i) – число объектов, обладающих свойством а_i, и вообще N(i₁, …, i_k) – число объектов, обладающих одновременно всеми свойствами . Пусть N(0) – число объектов, не обладающих ни одним из свойств а_i. Справедлива формула включения и исключения:

N(0) = N – + + …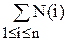

+ (– 1)^k + … + (–1)ⁿ N(1, 2, …, n). (3.1)

Символ 1 £ i₁ < i₂ <…< i_k £ n под знаком суммы означает, что суммирование ведется по всем комбинациям i₁, i₂,…, i_k так, чтобы выполнялось указанное соотношений. Доказательство проведем с помощью индукции по n – число свойств.

1⁰. n = 1. N(0) = N – N(1). Всего существует одно свойство. От общего числа объектов отнимем количество объектов, обладающих этим свойством – узнаем, сколько объектов этим свойством не обладают.

2⁰. Пусть для n – 1 свойств справедлива формула

N(0) = N – + + …

+ (– 1)^k + … + (–1)ⁿ N(1, 2, …, n – 1). (3.2)

Пусть теперь имеем множество, все элементы которого обладают свойством а_n, и, возможно, обладают свойствами а₁, …, а_n–1. Очевидно, для этого множества формула (3.2) также верна и имеет вид:

N(0, n) = N(n) – + … +

+(–1)^n–2 + (–1)^n–1N(1, 2, …, n – 1, n). (3.3)

В (3.3) везде в скобках дописано n, т.к. все элементы множества свойством а_n обладают. Вычтем (3.3) из (3.2):

N(0) – N(0, n) = N – + + … – (–1)^n–1 N(1, 2, …, n – 1, n).

Отсюда

N(0) – N(0, n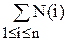) = N – + +… + (–1)ⁿ N(1, 2,…,n).

Справа мы получили требуемую формулу. А что слева? N(0) – число элементов, не обладающих свойствами а₁, …, а_n–1, но, возможно, обладающих свойством а_n. N(0, n) – число элементов, не обладающих свойствами а₁, …, а_n–1, но обязательно обладающих свойством а_n. Следовательно, N(0) – N(0, n) – число элементов, не обладающих ни одним из свойств а₁, …, а_n, т.е. требуемая величина. Формула доказана.

Пример 3.1. Староста класса подал следующие сведения о классе. Всего в классе 45 учеников, из них 25 мальчиков. 30 человек учится без троек, из них – 16 мальчиков; 28 человек занимаются спортом, из них – 18 мальчиков и 17 хорошистов и отличников; 15 мальчиков учатся без троек и одновременно занимаются спортом. Классный руководитель внимательно посмотрел список и сказал, что в сведениях есть ошибка. Как он это узнал?

Решение. Обозначим a₁ – свойство принадлежности к мужскому полу; a₂ – хорошая успеваемость; a₃ – занятие спортом. Тогда N = 45, N(1) = 25, N(2) = 30, N(3) = 28, N(1, 2) = 16, N(1, 3) = 18, N(2, 3) = 17, N(1, 2, 3) = 15. Итого N(0) = 45 – 25 – 28 + 16 + 18 + 17 – 15 = – 2 – ошибка.

1.2. Модификации формулы включения и исключения

2.а. Формулу (2.1) можно обобщить для определения числа элементов, обладающих в точности k свойствами (0 £ k £ n):

N(k) = + …+ (– 1)^s–k + …

+ (–1)^n–k ×N(1, 2, …, n). (3.4)

Пример 3.2. В отделе НИИ каждый сотрудник владеет хотя бы одним иностранным языком. Известно, что английским языком владеют 6 человек, немецким – 6, французским – 7, английским и немецким – 4, немецким и французским – 3, английским и французским – 2, все три языка знает 1 человек. Определить, сколько всего человек в отделе, сколько человек владеют только английским, только немецким, только французским, и сколько человек знает только 1 иностранный язык.

Решение. Согласно условиям задачи N(0) = 0, т.к. в отделе нет сотрудников, не владеющих иностранными языками. Следовательно, по формуле (3.1) получаем:

N = 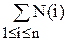– + N(1, 2, 3) (3.5)

N = 6 + 6 + 7 – 4 – 3 – 2 + 1 = 11 человек всего в отделе.

Для вычисления остальных показателей также воспользуемся формулой (3.5). Найдем, например N(только А) – число человек, не владеющих никаким другим языком, кроме английского. Для этого формулу (3.5) надо применить только к множеству людей, владеющих английским языком. В этом случае n = 2. Тогда N = N(A), N(1) и N(2) – число людей, владеющих помимо английского еще немецким и французским, соответственно, N(1, 2) – число людей, владеющих помимо английского еще одновременно немецким и французским. Отсюда

N(только A) = N(A) – N(А и Н) – N(А и Ф) + N(А и Н и Ф) =

6 – 4 – 2 + 1 = 1.

Аналогично

N(только Н) = N(Н) – N(А и Н) – N(Н и Ф) + N(А и Н и Ф) =

6 – 4 – 3 + 1 = 0.

N(только Ф) = N(Ф) – N(Ф и А) – N(Ф и Н) + N(А и Н и Ф) =

7 –2 – 3 + 1 = 3.

Вычислим теперь N(1) – число людей, владеющих только 1 языком. Воспользуемся формулой (3.4) при k = 1.

N(1) = N(А) + N(Н) + N(Ф) + (–1)^2–1× × [N(А и Н) + N(Н и Ф) + N(А и Ф)] + (–1)^3–1× × N(А и Н и Ф) = 6 + 6 + 7 – 2×(4 + 3 + 2) + 3×1 = 4.

Такой же результат получим, если сложим N(только A) + N(только Н) + N(только Ф).

2.б. Формулу (3.1) можно также интерпретировать, как подсчет мощностей пересечений различных множеств, т.е. дать теоретико-множественное представление принципа включения и исключения. Пусть имеем некоторое конечное множество А и его подмножества А_j, j = 1,…, n. Тогда теоретико-множественный аналог формулы (3.1) будет иметь вид:

= |A| – + + …

+ (– 1)^k + …+ (–1)ⁿ .

 

Формулы обращения

2.1. Теорема обращения. Пусть имеем два семейства комбинаторных чисел {a_n,k} и {b_n,k}, зависящих от целочисленных параметров n, k, причем 0 £ k £ n.

Теорема 3.1. Пусть для любых n и k, 0 £ k £ n справедливы зависимости и пусть существуют такие числа m_n,k,i, что для любых k £ n и m £ n выполняются равенства

Тогда для всех k £ n имеет место формула обращения:

.

Доказательство.

= = = b_n,k,

что и требовалось доказать.

2.2. Примеры использования формулы обращения. Зависимость между числами l_n,k,i и m_n,k,i, фигурирующая в условиях теоремы 3.1, по сути означает, что эти числа образуют систему взаимно обратных матриц, т.е. смысл теоремы весьма прост, если не сказать – тривиален. Для произвольных чисел a_n,k и b_n,k она не дает никакой ценной информации, поскольку найти требуемые числа m_n,k,i в общем случае столь же трудно, как и решить исходную систему уравнений относительно b_n,k. Однако, для многих специальных случаев, в частности, комбинаторных чисел, удается найти m_n,k,i в явном виде. В этом особенность данной формулы. Рассмотрим ее применение для обращения биномиальных коэффициентов.

Лемма 3.1.

Доказательство. Имеем:

= =

= = .

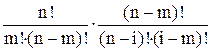Следовательно,

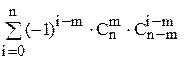= = В.

Так как при k < 0 и при k > n , то в полученном выражении можно суммировать не от i = 0, i = m. То есть

В = = .

Но при m < n имеем:

= = 0.

Последнее равенство следует из свойства 5 чисел сочетания.

А при m = n имеем:

= = 1,

что и требовалось доказать.

Теорема 3.2. Если , то .

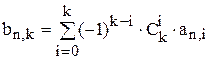Доказательство. Здесь и . При k £ n, m £ n имеем:

= = = =

Это означает, что выполнены условия теоремы 3.1, а, следовательно, теорема доказана.

Теорема 3.3. Если , то .

Доказательство аналогично.

 

Рекуррентные соотношения

В комбинаторных задачах искомым решением часто является числовая последовательность u₁, u₂, …, u_n, … Например, если мы ищем число подмножеств m-элементного множества, то . В данном разделе рассмотрим ситуацию, при которой свойства членов искомой последовательности определяются некоторым рекуррентным соотношением, которому удовлетворяют числа u_n:

u_{n + k} + b₁ u_{n + k – 1} + b₂ u_{n + k – 2} +…+ b_k u_n = 0, (3.6)

где b₁, b₂, …, b_k – некоторые коэффициенты. Выражение (3.6) называется еще разностным линейным уравнением k-го порядка с постоянными коэффициентами.

Одной из наиболее известных последовательностей, задаваемых линейным рекуррентным соотношением, является последовательность Фибоначчи {F_n}, определяемая следующими условиями: F₀ = 0; F₁ = 1; F_n+2 = F_n+1 + F_n. Отсюда получаем F₂ = 1; F₃ = 2; F₄ = 3; F₅ = 5; F₆ = 8 и т.д.

Воспользовавшись уравнением (2.8) всегда можно вычислить значения u_n для любых n, если знать первые k членов последовательности. Однако, часто необходимо знать явную формулу для вычисления u_n.

Теорема 3.4. Пусть l₁, l₂,…, l_s – корни соответствующих кратностей m₁, m₂,…, m_s характеристического уравнения для выражения (3.6):

l^k + b₁ l^k–1 + b₂ l^k–2 +…+ b_k = 0 (3.7)

Тогда общее решение уравнения (3.6) определяется по формуле:

u_n = (C₁₁ + C₁₂ ×n + C₁₃×n² + … + ) +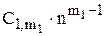

(C₂₁ + C₂₂ ×n + C₂₃×n² + … + 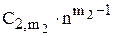) + … (3.8)

(C_s,1 + C_s,2 ×n + C_s,3×n² + … + ) ,

где C₁₁,…, – константы (их число равно k), определяемые начальными условиями.

Пример 3.3. Решим уравнение Фибоначчи F_n+2 – F_n+1 – F_n = 0. Его характеристическое уравнение имеет вид: l² – l – 1 = 0. Корни равны – некратные. Обозначим Ф₁ = l₁ » 1.618; Ф₂ = l₂ » – 0.618. Общее решение равно:

.

Из начальных условий F₀ = 0; F₁ = 1 получаем систему уравнений для вычисления С₁ и С₂ = 1:

.

Отсюда С₁ = – С₂ = .

Использование рекуррентных соотношений дает эффективный метод решения многих комбинаторных задач.

Пример 3.4. Найти число бинарных n-последовательностей, в которых никакие две единицы не стоят рядом.

Решение. Обозначим:

z_n – число искомых последовательностей;

х_n – число последовательностей, заканчивающихся 0;

у_n – число последовательностей, заканчивающихся 1.

Назовем для краткости последовательность, заканчивающуюся 0 – х-последовательностью, а заканчивающихся 1 – у-последовательностью.

Очевидны следующие их свойства.

1) х-последовательность длиной n можно получить, приписав 0 в конец либо у-последовательности либо х-последовательности длиной n – 1.

2) у-последовательность длиной n можно получить, приписав 1 только в конец х-последовательности длиной n – 1.

Отсюда имеем следующую систему уравнений:

.

Уравнение (a) отражает свойство 1), уравнение (b) – свойство 2), а уравнение (а) соответствует очевидному равенству.

Из уравнения (b) при замене n на n – 1 имеем: у_n–1 = х_n–2.

Подставим это равенство в (a), получим: х_n = х_n–1 + х_n–2, т.е. числа х_n образуют последовательность Фибоначчи. Вычтем (b) из (a), получим:

х_n – у_n = у_n–1 Þ х_n = у_n + у_n–1 Þ у_n+1 = у_n + у_n–1

– тоже последовательность Фибоначчи. В соответствие с формулой общего решения и уравнением (c) получим:

.

Для нахождения констант запишем начальные условия. z₁ = 2, т.к. существует 2 последовательности длиной 1: 0 и 1. z₂ = 3, т.к. существует 3 последовательности длиной 2: (0 0), (0 1), (1 0). Отсюда ; . Следовательно

_.

Например, z₉ = 89, z₁₉ = 10946.

 

Производящие функции

4.1. Определение производящих функций. Последовательности {u_n}, фигурирующей в какой-либо задаче, например, комбинаторной, удобно поставить в соответствие формальный степенной ряд

u(x) = ,

который называется производящей функцией данной последовательности. Слова “формальный ряд” означает, что эту формулу мы трактуем только как удобную запись последовательности. Для нас сейчас несущественно, при каких значениях х ряд сходится и сходится ли вообще, т.к. вычислять значение u(x) мы никогда не будем.

Пример 3.5. Известно, что = 1 + х + х² + … + хⁿ + … Следовательно, функция является производящей для последовательности 1,…, 1.

Пример 3.6. Согласно формуле бинома Ньютона (1 + х)ⁿ = . Следовательно, функция (1 + х)ⁿ является производящей для конечной последовательности .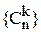

4.2. Операции с производящими функциями. Рассмотрим основные технические приемы, применяемые в работе с производящими функциями.

4.2.а. Линейная комбинация. Если функция u(x) соответствует последовательности {u_n}, а v(x) – последовательности {v_n}, то функция a×u(x) + b×v(x) (a и b – константы) является производящей для последовательности { a×u_n + b×v_n}.

4.2.б. Сдвиг. Если функция u(x) соответствует последовательности {u_n}, то функции х^m×u(x) соответствует последовательность … – сдвиг вправо.

Аналогично, функция является производящей для последовательности u_m, u_m+1, … – сдвиг влево.

4.2.в. Умножение. Если функция u(x) соответствует последовательности {u_n}, а v(x) – последовательности {v_n}, то функции u(x)×v(x) соответствует последовательность {w_n}, где

– формула Коши. Например, w₀ = u₀×v₀; w₁ = u₀ ×v₁ + u₁ ×v₀; w₂ = u₀ ×v₂ + u₁ ×v₁ + u₂ ×v₀.

Пример 3.7. Пусть u(x) соответствует последовательности {u_n}, а v(x) = – производящая функция для последовательности 1,…, 1 (см. пример 3.5). Тогда функция

= u₀ + (u₀ + u₁) x + (u₀ + u₁ + u₂) x² +… (3.9)

является производящей для последовательности частичных сумм.

4.2.г. Дифференцирование и интегрирование. Если u(x) соответствует последовательности {u_n}, то по правилу дифференцирования рядов

u¢(x) = 0 + u₁ + 2 u₂ x + 3 u₃ x² + ….

То есть u¢(x) является производящей функцией для последовательности {k u_k}.

Аналогично 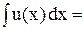. То есть является производящей функцией для последовательности .

Пример 3.8. = 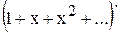. Следовательно, функция является производящей для последовательности {k}.

Далее,

(3.10)

Следовательно, является производящей функцией для последовательности .

Сопоставляя (3.10) с (3.9) получаем

,

где 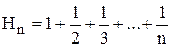– гармонические числа.

4.3. Пример использования производящих функций

Решим с помощью производящих функций следующую комбинаторную задачу.

Пример 3.9. На окружности находится 2n точек. Сколькими способами можно их попарно соединить так, чтобы полученные отрезки не соединялись друг с другом?

Решение. Обозначим u_n – число способов соединить 2n точек. Построим рекуррентное соотношение.

Формально положим u₀ = 1 (нет точек, нет пересечений, следовательно, способ единственный). u₁ = 1 – очевидно, т.к. две точки соединяются единственным способом, и пересечений нет. u₂ = 2. Способы соединения изображены на рис. 3.1.

		Рис. 3.1. Способы соединения 4-х точек

 

 

Пусть n > 1. Выберем одну из 2(n + 1) точек, обозначим ее А. Соединим А с вершиной В, выбрав ее так, чтобы с обеих сторон от соединяющей их линии находилось четное число точек. Пусть слева будет 2k точек, справа – 2(n – k). 2k точек можно соединить между собой u_k способами, 2(n – k) точек – u_n–k способами. При этом линии не пересекутся, т.к. 2k и 2(n – k) точек расположены по разные сторона от АВ.

Следовательно, при фиксированном k получим u_k×u_n–k способов соединения. Но k меняется от 0 до n. Следовательно,

u_{n +1} = u₀×u_n + u₁×u_n–1 + … + u_n×u₀. (3.11)

Получили искомое нелинейное рекуррентное соотношение, формула общего решения которого нам, к сожалению, неизвестна.

Чтобы получить явную формулу для u_n, построим для этой последовательности производящую функцию.

u(x) = u₀ + u₁х + u₂ x² + u₃ x³ + …. (3.12)

 

Имеем, согласно формуле Коши:

[ u(x) ]² = (u₀)² + (u₀×u₁ + u₁×u₀) х + (u₀×u₂ + u₁×u₁ + u₂×u₀)х² + …

Видно, что коэффициенты для разложения [ u(x) ]² можно получить с помощью формулы (3.11).

Из (3.12) имеем: = u₁ + u₂ x + u₃ x² + ….

Подставим в эту формулу выражение u_k согласно (3.11). С учетом того, что u₁ = (u₀)² получим: . Следовательно, имеем квадратное уравнение относительно u(х). Решив его, получим .

По формуле бинома имеем:

+ +…= 1 – .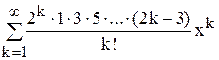

 

Умножим каждое k-е слагаемое на 1 = . Тогда коэффициент k-го члена ряда равен:

= = = .

Отсюда

.

Для того, чтобы коэффициенты ряда были положительными, надо перед корнем в формуле u(x) брать знак “–”. Заменим индекс суммирования k на k +1. В результате получим:

u(x) = = = .

Окончательно – это так называемые, числа Каталана.

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: