Определение напряжений и деформации при кручении круглого стрежня.

СДВИГ (СРЕЗ).

Понятие о сдвиге.

Если на стержень приложить две силы, равные по величине и близко расположенные друг к другу в противоположном направлении (как это бывает при перерезывании ножницами) то возникает сдвиг или срез.

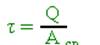- касательные напряжения. - проверка прочности

где Q-перерезывающая сила равна P; A_ср-площадь среза; R_ср- расчетное сопротивление материала на срез.

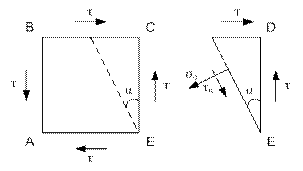
Если по граням элемента, выделенного из тела, действуют только касательные напряжения, то такой сдвиг называется чистым.

Деформация при чистом сдвиге. Анализ напряженного состояния.

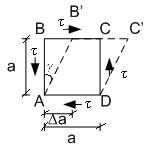
Если грань AD закреплена, то под действием касательного напряжения элемент получит деформации и примет форму AB'C'D

– абсолютный сдвиг,

tg γ=∆а/а ≈ γ, т.е. очень маленький угол.

tg γ – относительный сдвиг.

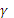– угол сдвига

Установлено, что между напряжением τ и углом γ существует линейная зависимость, называемая законом Гука при сдвиге: τ=G∙ γ

G – модуль сдвига (модуль упругости второго рода)

- закон Гука при растяжении.

G=0,4Е - соотношение между G и Е.

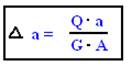– закон Гука при сдвиге в другом виде.

G∙A – жесткость при сдвиге.

Анализ напряженного состояния при чистом сдвиге.

 

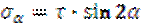
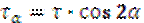
Рассмотрим чистый сдвиг: Вывод: если внутри элемента, по граням которого действуют касательные напряжения (чистый сдвиг) выделить другой элемент, то по граням этого элемента, повернутого на угол 45° относительно исходных граней возникают только нормальные напряжения, причем в одном направлении они будут растягивающими, а в другом сжимающими. Эти нормальные напряжение σ равны касательным τ.

 

Зависимость между 3-мя упругими постоянными G, Е, μ.

Между упругими постоянными существует следующая зависимость: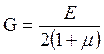

КРУЧЕНИЕ.

Построение эпюр крутящих элементов методом сечений.

Крутящий момент Mк в сечении равен сумме моментов слева или справа от сечения.

Правило знаков: Крутящий момент (M_к) считается положительным если окажется, что при взгляде на сечение со стороны нормали момент направлен против часовой стрелки.

 

Пример 1. Дано: М₁ =1кН∙м; М₂=2кН∙м; М₃= 3кН∙м

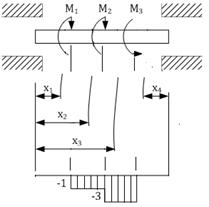
сеч. 1: Мк=0 сеч. 2: Мк= - М1 = - 1 кН·м сеч. 3: Мк= - М1 - М2 = - 1 – 2 = - 3 кН·м сеч. 4: Мк= - 1 – 2 + 3 = 0

Связь между крутящим моментом, мощностью и числом оборотов

W=Мк∙ω=Мк ∙π∙n/30 (кГ∙м/сек),

где ω – угловая скорость, n – число оборотов в сек..

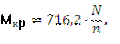
–мощность, л/с

(кГс∙м).

–мощность, кВт (киловатт)

М кр=9,736∙N/n, (кН∙м)

где – число оборотов в минуту.

1л/с=0,736кВт.

Определение напряжений и деформации при кручении круглого стрежня.

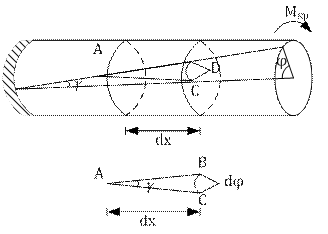
При кручении круглого стержня замечаем:

1) При деформации поперечные сечения не искривляются, а остаются плоскими.

2) Расстояние между поперечными сечениями не изменяются.

3) Радиусы при деформации не искривляются.

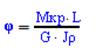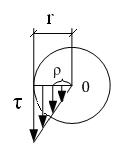
-угол поворота в радианах. -угол поворота в градусах. Jρ –полярный момент инерции. - касательное напряжение на расстоянии ρ от центра τmax = Мкр ∙r/ Jρ

– полярный момент инерции круга

Wρ= Jρ/ r – полярный момент сопротивления

Wρ= π∙d⁴/ 16 - полярный момент сопротивления круга.

Mк/ Wρ ≤[τ ] – проверка прочности при кручении.

 

Mк/ Wρ ≤ R_s проверка прочности при срезе,

где - расчетное сопротивление на срез.

Жесткость при кручении проверяется:

где 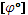- допускаемый угол поворота на длине равной единице.

Рассмотрим напряжения в круглом стержне:

1) На основании закона парности касательных напряжений в стержне при кручении появляются касательные напряжения, направленные вдоль оси сечения. 2) Под углом 45°в стержне возникают нормальные напряжения, при чем: σ = τ

 

 

Кручение стержня прямоугольного сечения.

 

Для наглядности берем призматический стержень прямоугольного сечения из резины, на боковых поверхностях которого нанесена сетка.

 

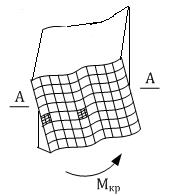
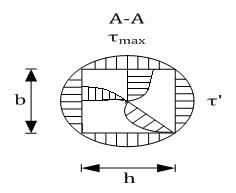
При деформации замечаем:

1) Плоские сечения при деформации не остаются плоскими, а в круглом – остаются.

2) В углах стержня прямоугольники не искажаются → здесь касательное напряжение отсутствуют.

3) Наибольшее искажение получает прямоугольник сетки, расположенный в середине широкой стороны прямоугольника, здесь возникает максимальное касательное напряжение.

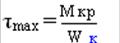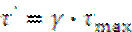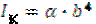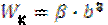, , , – формулы для прямоугольного сечения.

– зависят от соотношения сторон и приводятся в специальных таблицах.

 

Поделиться:

Воспользуйтесь поиском по сайту: