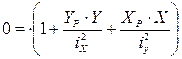|
Нулевая линия делит сечение на две части: на одной стороне, возникают сжимающие напряжения, а на другой растягивающие.
|
|
|
|
Косой изгиб.
Деформация косого изгиба возникает при действии нагрузок не проходящих через главные оси инерции поперечного сечения.
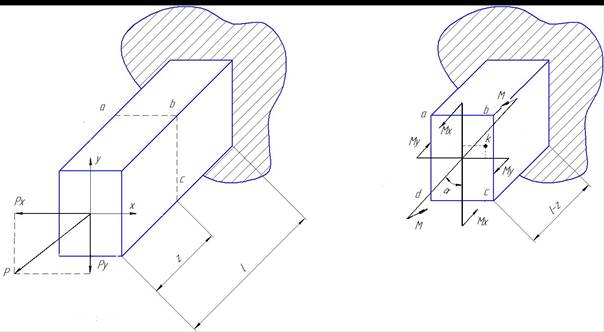
Силу Р раскладываем на составляющие Рх и Ру: 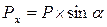 . Изгибающий момент в сечении авсd будет
. Изгибающий момент в сечении авсd будет 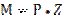 ;
;  ; Му=Рх*Z;
; Му=Рх*Z; 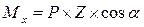 ;
; 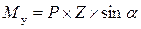 .
.
Нормальные напряжения в любой точке К с координатами (Хк;YK). Получим на основе принципа независимости действия сил, как сумму напряжений от Мх и Му, действующих по главным осям инерции:

| (1) |
| Напряжения в угловых точках будут определяться по формулам: | 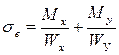 ; ; 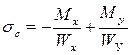 ; ; 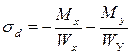 ; ; 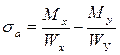 . .
|
В формулу (1) представим в другом виде: 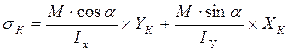 (2). Что касается стержнем произвольного поперечного сечения, то отыскания наиболее опасных точек производится следующим образом:
(2). Что касается стержнем произвольного поперечного сечения, то отыскания наиболее опасных точек производится следующим образом:
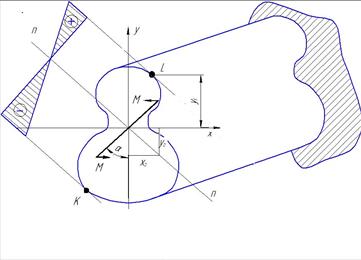
| В начале находится положение нулевой линии, т.е. геометрического места точек, где нормальные напряжения равны нулю. 1)Предположим, что нулевая линия проходит через (nn). 2)Затем, учитывая, что по мере удаления от нулевой линии напряжения возрастают, заключаем, что наиболее опасными точками являются точки L и K. 3)Проводим через L и K линии, параллельные линии (nn) и строим эпюру σ. |
Для определения положения нулевой линии (nn) правую часть формулы (2) приравняем к нулю: 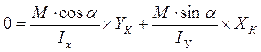 поделим на
поделим на 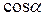 :
: 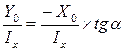 ; поделим это выражение на Х0 :
; поделим это выражение на Х0 : 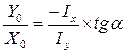 . Из чертежа:
. Из чертежа: 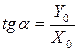
| (3)По формуле (3) находится положение нулевой линии.
Вывод: если 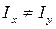 , то , то 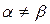 , это означает, что угол наклона нулевой линии не перпендикулярен к линии действия нагрузки. , это означает, что угол наклона нулевой линии не перпендикулярен к линии действия нагрузки.
| |||||
| Наибольшие напряжения будут в точках L и K. Прочность стержня проверяется по формулам: |
| |||||
 Для симметричного сечения условие прочности можно записать так:
Прогиб при косом изгибе находится как геометрическая сумма двух прогибов: Для симметричного сечения условие прочности можно записать так:
Прогиб при косом изгибе находится как геометрическая сумма двух прогибов:
|
где
| |||||
Внецентренное сжатие (растяжение).
Если сжимающая сила не проходит через центр тяжести поперечного сечения стержня, то стержень будет испытывать внецентренное сжатие (растяжение).
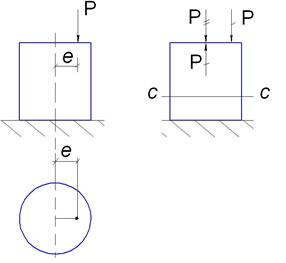
| Для расчета стержня приложим в центре тяжести поперечного сечения две силы Р противоположно направленные. Тогда сила Р зачеркнутая дважды вызывает осевое сжатие, а пара сил зачеркнутых однажды создают момент равный Р×е=М(чистый изгиб). Как нам известно при осевом сжатии и при чистом изгибе напряжения во всех сечениях будет одинаковые, поэтому рассмотрим произвольное сечение (сс). Отбросим верхнюю часть и рассмотрим оставшуюся нижнюю. | |
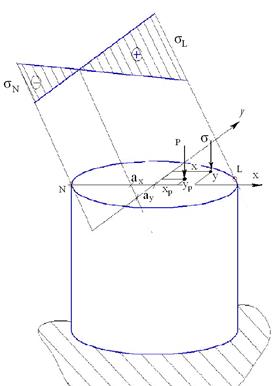
| Найдем напряжение σ в точке К (X;Y). Эти напряжения складываются из напряжений от осевого сжатия и от напряжений чистого изгиба. При осевом сжатии напряжения будут равны (-Р/A). Что касается чистого изгиба, мы его разложим на два изгиба, действующих по главным осям инерции.
От изгибающего момента 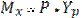 напряжения будут напряжения будут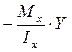 .От момента .От момента 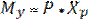 имеем напряжение имеем напряжение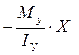 . Суммарное напряжение равно: . Суммарное напряжение равно:

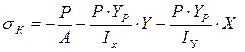
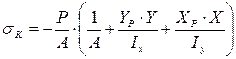
| |
 (1) (1)
| ||
По формуле (1) можно найти напряжение в любой точке поперечного сечения для этого следует координаты X и У подставить с учетом их знака.
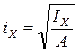 ; ; 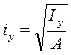
|
Формула (1) справедлива также и при растяжении. В этом случае вместо (-) имели бы (+) перед формулой, где:
– радиусы инерции.
Найдем положение нулевой линии. Для этого приравняем правую часть формулы (1) к нулю.
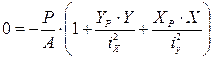 ;
; 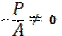 ; значит
; значит
| - уравнение нулевой линии, которая является прямой линией. |
Поэтому для нахождения положения нулевой линии найдем отрезки, отсекаемые ею на осях Х и У. Для чего принимаем у=0; х=ах. подставив в уравнение получим 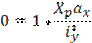
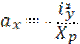 - отрезок отсекаемый нулевой линией на оси Х. - отрезок отсекаемый нулевой линией на оси Х.
|
Примем 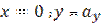 , получим
, получим
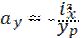 - отрезок отсекаемый нулевой линией на оси У. - отрезок отсекаемый нулевой линией на оси У.
|
Нулевая линия делит сечение на две части: на одной стороне, возникают сжимающие напряжения, а на другой растягивающие.
|
|
|
Прочность при внецентренном сжатии (растяжении) проверяется по формулам:
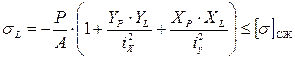 (или ≤Rcж). (или ≤Rcж). 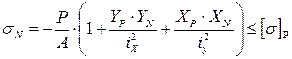 (или ≤Rр), где ХL и YL - координаты точки L; ХN и УN - координаты точки N. (или ≤Rр), где ХL и YL - координаты точки L; ХN и УN - координаты точки N.
|
Ядро сечения
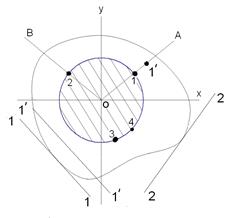
| Как видно положение нулевой линии зависит от координат 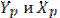 . Если сила приложена в точке 1/; то нулевая линия пройдет по (1/;1/). Если точку приложения силы перемещать вдоль луча ОА, то нулевая линия будет также перемещаться, оставаясь параллельно самой себе. Таким образом можно найти такую точку 1 для которой нулевая линия коснётся контура сечения будет (1;1). Таким же образом можно на луче ОВ найти точку 2, для которой нулевая линия пройдет по (2;2). В итоге приняв несколько точек 1;2;3;4… и соединив их получим ядро сечения. . Если сила приложена в точке 1/; то нулевая линия пройдет по (1/;1/). Если точку приложения силы перемещать вдоль луча ОА, то нулевая линия будет также перемещаться, оставаясь параллельно самой себе. Таким образом можно найти такую точку 1 для которой нулевая линия коснётся контура сечения будет (1;1). Таким же образом можно на луче ОВ найти точку 2, для которой нулевая линия пройдет по (2;2). В итоге приняв несколько точек 1;2;3;4… и соединив их получим ядро сечения.
|
Ядро сечения – это область, очерченная вокруг центра тяжести и обладающая теми свойствами, что если приложить внутри этой области силу, то все поперечное сечение стержня будет иметь напряжение одинакового знака.
Для построения ядра сечения следует провести несколько линий касающихся контура сечения, вычислить для этих линий aх и aу, а затем найти значения 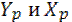 по формулам:
по формулам: 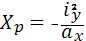 ;
; 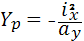
Пример1. Найти ядро сечения для прямоугольника.

| 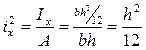 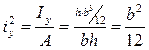 Проведем линию (1-1):
Проведем линию (1-1): 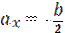 ; ; 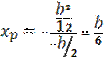 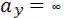 ; ; 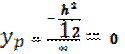 Линия (2-2): Линия (2-2): 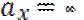 ; ; 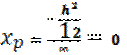 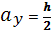 ; ; 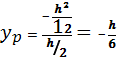 Аналогично получаем 3 и 4 точки.
Аналогично получаем 3 и 4 точки.
|
|
|
|



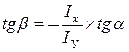
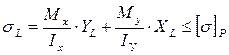 (или ≤ Rр)
(или ≤ Rр)
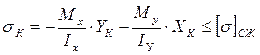 (или ≤ Rсж)
(или ≤ Rсж)
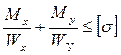 (или ≤R)
(или ≤R)
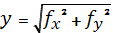
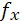 – прогиб в плоскости оси Х от силы Р х ;
– прогиб в плоскости оси Х от силы Р х ; 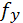 – прогиб в плоскости оси У от силы Р у.
– прогиб в плоскости оси У от силы Р у.