 |
Практическая формула для расчета на устойчивость.
|
|
|
|
ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ.
Раньше при сжатии стержня прочность проверяли по формуле:
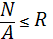 ; или
; или 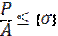 – по допускаемым напряжение.
– по допускаемым напряжение.
Эти формулы предполагают, что все время вплоть до разрушения стержень работает на осевое сжатие. Однако, если имеем дело с длинным стержнем, то разрушение произойдет при напряжениях значительно меньших, чем при сжатии короткого стержня (от потери устойчивости). Записанные выше формулы справедливы только для коротких стержней. Рассмотрим поведение длинного стержня под нагрузкой.
Здесь различают 3 состояния:
1) устойчивое состояние, когда стержень под действием нагрузки сохраняет первоначальную форму. Если этот стержень незначительно отклонить какой-либо поперечной силой, а затем убрать эту силу, то он примет первоначальное положение.
2) безразличное состояние – это такое состояние, когда стержень может находиться в любом положении: а) в первоначальном; б)если отклонить незначительно, то остается в отклоненном положении. Нагрузка соответствующая этому состоянию называется критической.
3) неустойчивое состояние – это такое состояние, когда нагрузка больше критической - происходит разрушение
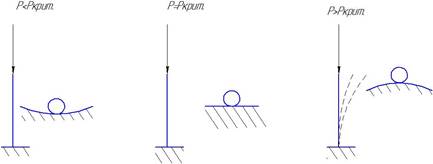
Для инженера интерес представляет безразличное состояние, т.е. ytj,[jlbvj научиться находить силу Р при которой стержень начинает разрушаться.
Критическая сила при осевом сжатии. (формула Эйлера)
: Критическая сила может иметь бесчисленное множество значений.
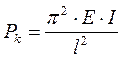 – формула Леонардо-Эйлера – формула Леонардо-Эйлера
|
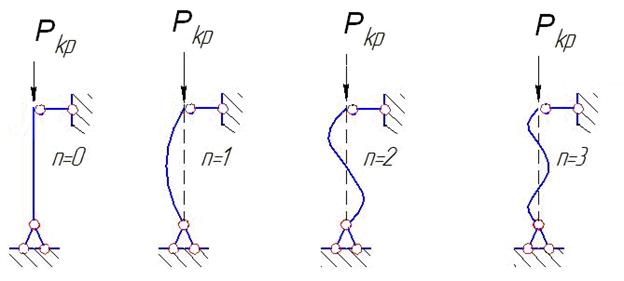
Инженера интересует наименьшее значение критической силы, когда n=1
Влияние способа закрепления концов стержня на величину критической силы.
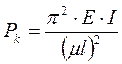
|
При других способах закрепления концов стержня критическая сила определяется по формуле:
|
|
|
где 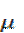 - коэффициент приведения длины, зависящий от способа закрепления концов стержня. Значения
- коэффициент приведения длины, зависящий от способа закрепления концов стержня. Значения 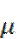 приведены на рисунках.
приведены на рисунках.
 Критические напряжения и пределы применения формулы Эйлера.
Критические напряжения и пределы применения формулы Эйлера.
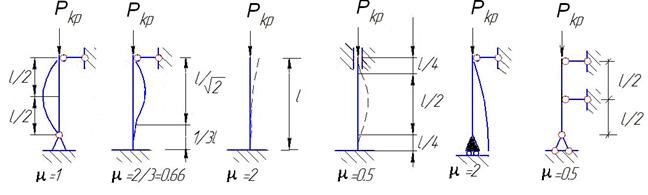
σкр = Ркр /А - критическое напряжение, где А – площадь поперечного сечения стержня.
обозначим 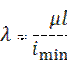 , где λ - гибкость стержня,
, где λ - гибкость стержня, 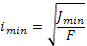 - наименьший радиус инерции.
- наименьший радиус инерции.
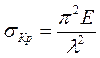
|
После подстановки получим критическое напряжение:
Формулой Эйлера не всегда можно воспользоваться.
Вывод формулы Эйлера исходит из уравнения ЕI y//=M, где Е- модуль упругости материала. 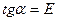 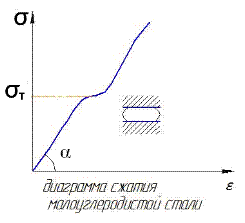
| Как видно из диаграммы за пределом пропорциональности модуль упругости меняет свою величину, поэтому формулу Эйлера нельзя применять при напряжениях превышающих предел пропорциональности. |
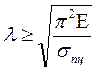
|
 – пределы применимости формулы Эйлера.
– пределы применимости формулы Эйлера.
Пояснение: когда λ найденная по формуле 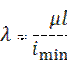 окажется больше чем
окажется больше чем 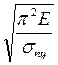 можно использовать формулу Эйлера для определения σкр..
можно использовать формулу Эйлера для определения σкр..
Например, для стержня, изготовленного из стали с пределом пропорциональности
σпц = 200 МПа = 20кн/см2, Е =2,1∙106 кг/см2 =2,1 ∙ 104 кн/см 2 можно пользоваться формулой Эйлера при гибкости: 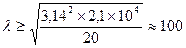 т.е. для стали 3 при
т.е. для стали 3 при 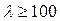 справедлива формула Эйлера.
справедлива формула Эйлера.
Аналогичным образом получим условия применимости формулы Эйлера для чугуна: 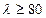 .
.
Для стержней малой и средней гибкости в результате экспериментальных исследований Ф. Ясинский получил формулы:
σкр= σО. – для стержней малой гибкости при λ=(0÷100)
σкр= σтек – для пластичных материалов
σкр= σпч – для хрупких материалов
σкр= а-в∙λ – формула Ясинского, где а и b - коэффициенты, зависящие от материала;
где а=3100кг/см2 b =11,4кг/см2. - для стержней из стали 3.
(или а=2400кг/см2 b =4кг/см2- по новым результатам исследований для мягко пластичных сталей).
Формула Ясинского применима для стержней средней гибкости λ=60÷100 для стали 3.
Имея формулы Эйлера и формулы Ясинского можно построить график зависимости λ от σкр..
|
|
|
Практическая формула для расчета на устойчивость.
Вместо двух формул Эйлера и Ясинского удобно иметь одну. Выведем эту практическую формулу. Известно, что прочность стержня, нагруженного осевой силой Р, можно проверить по формуле 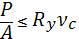 , где
, где 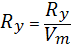 .
.
На устойчивость проверим по формуле 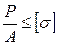 . Обозначим
. Обозначим 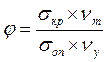 получим
получим 
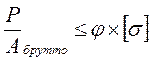 (3) (3)
|
- проверка устойчивости при расчете по допускаемым напряжениям.
| - проверка устойчивости при расчете по расчетным сопротивлениям, где Rу – предел текучести (расчетное сопротивление). Абрутто – площадь поперечного сечения брутто (без учета ослаблений). |
По формулам 3 и 4 проверяется стержень на устойчивость, кроме этого не следует забывать, что стержень необходимо проверить еще на прочность по формуле:
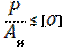 (по допускаемым напряжениям) или
(по допускаемым напряжениям) или 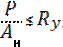 (по расчетным сопротивлениям).
(по расчетным сопротивлениям).
Ан – площадь поперечного сечения нетто (с учетом ослаблений, отверстий и т.д.)
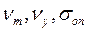 – постоянные величины для данного материала. Поэтому
– постоянные величины для данного материала. Поэтому  будет зависеть от σкр. Учитывая, что между σкр. и λ существует зависимость следующего вида
будет зависеть от σкр. Учитывая, что между σкр. и λ существует зависимость следующего вида 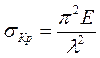 , то можно составить график зависимости
, то можно составить график зависимости  .
.
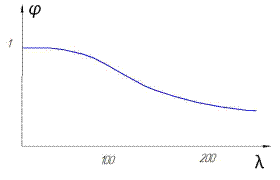
| Графики зависимости  построены для многих строительных материалов. Иногда они приводятся в виде таблиц. построены для многих строительных материалов. Иногда они приводятся в виде таблиц.
|
По формулам (3 и 4) можно подобрать сечение стержня. Для этого поступают следующим образом:
Алгоритм подбора сечения.
1) задаемся значением φ =0,6÷0,7
2) по формуле 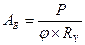 определяютАБ
определяютАБ
3) принимают по значениямАБ размеры поперечного сечения (для прокатных профилей по сортаменту)
4) определить минимальный радиус инерции поперечного сечения imin
5) определить гибкость 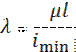
6) по таблице (или по графику зависимости 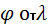 находят значение
находят значение 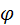 )
)
7) после этого осуществляют проверку по формуле 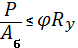 или
или 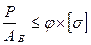
8) если это условие не удовлетворяется, то задаются другим значением 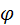 и расчет повторяют, при этом не допускается большой запас устойчивости.
и расчет повторяют, при этом не допускается большой запас устойчивости.
Пример: Подобрать двутавровое сечение из стали 3, центрально сжатой колонны заделанной одним концом, при другом свободном конце. Дано: расчетная сжимающая сила Р=1200 кг; L=2м, Rу=21 кн/см2 Решение.
Принимаем φ=0,6; 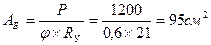
по сортаменту принимаем двутавр N50 (A=100 см 2 imin =3,23 см ; imах =19,9 см
Определяем гибкость 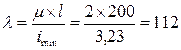 по таблице находим φ = 0,428
по таблице находим φ = 0,428
|
|
|
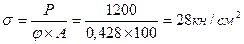 >21 не удовлетворяет проверке
>21 не удовлетворяет проверке
Вторая попытка: пусть φ=0,5; 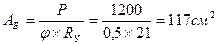
по сортаменту принимаем двутавр N55 (A=118 см 2 imin =3,39 см
Определяем гибкость 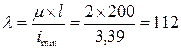 по таблице находим φ = 0,499
по таблице находим φ = 0,499
проверка: 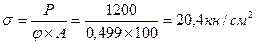 ≤21 кн/см2 - это сечение удовлетворяет нагрузке
≤21 кн/см2 - это сечение удовлетворяет нагрузке
|
|
|



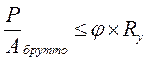 (4)
(4)