 |
Краткое теоретическое введение
|
|
|
|
ИЗУЧЕНИЕ РЕАЛЬНОГО ГАЗА (Эффект Джоуля-Томсона)
Цель работы
Целью лабораторной работы является экспериментальное определение изменения температуры воздуха в процессе адиабатного дросселирования при перепаде давления на дросселе до 12 атмосфер, а также определить внутреннее давление Газа, применяя для воздуха модель реального газа Вэн-дер-Ваальса.
Краткое теоретическое введение
В 1852 - 1862 гг. совместно Джоулем и В. Томсоном был выполнен целый ряд экспериментальных работ по исследованию термодинамических свойств Газов. В этой серии работ ими был обнаружен эффект названный в последствии эффектом Джоупя-Томсона.
| схематическое изображение опыта Джоуля-Томпсона: | ||||
| 1 – теплоизолирующая оболочка; 2-пористая перегородка; 3-цилиндрическая труба |
В опыте Джоуля и Томсона цилиндрическая трубка, окруженная теплоизолирующим веществом, разделяется на две части с помощью пробки из плотного материала (вата или очесы щелка). Схема опыта представлена на рисунке 1. Исследуемый газ под действием разности давлений медленно перетекает через пробку. Благодаря наличию пробки газ течет без турбулентности. Это позволяет пренебречь кинетической энергией газа как величиной, пропорциональной квадрату скорости. Наличие тепловой защиты делает процесс адиабатическим. Давление газа Р1 и P2 по обе стороны от пробки поддерживается постоянным. Пробка и газ обмениваются теплом до тех пор, пока процесс не становится стационарным, после этого физическое состояние пробки, а значит и ее внутренняя энергия, остается неизменным. При стационарном течении газа по одну сторону пробки устанавливалась температура t1, по другую - температура t2. Стационарное течение газа через пробку называется процессом Джоуля-Томсона, а изменение температур при таком течении эффектом Джоуля-Томсона.
|
|
|
Применим к эффекту Джоуля-Томсона первое начало термодинамики. Помня, что процесс адиабатический (т.е. газ не получает тепла, состояние пробки и ее внутренняя энергия не изменяются), можно записать

Заметим, что из уравнения (1.1) следует постоянство энтальпии (I=U+РТ) в процессе Джоуля-Томсона Используем это свойство для определения разности температур DT в процессе Джоуля-Томсона при разности давлений DP:
 |
Дпя дальнейшего использования формулы (1.2) необходимо определить уравнение состояния. В частности, для идеального газа числитель выражения в правой части (1.2) обращается в ноль.
Рассмотрим более реалистическое приближение для уравнения состояния.
 |
Kaк известно, неточность законов идеального газа объясняется существованием межмолекулярных сил, которыми пренебрегают в модели идеального газа. Из опыта мы знаем, что потенциальную энергию межмолекулярного взаимодействия можно приближенно представить в виде потенциала Ленарда-Джонса:
здесь a1 и a2 - положительные константы. Отсюда видно, что на малых расстояниях межмолекулярные силы носят резко отталкивающий характер, а на больших расстояниях – притягивающий. Для учета этих особенностей молекулярного взаимодействия в модели газа Ван-дер-Ваальса вводят две поправки.
Первая поправка связана с взаимодействием молекул на малых расстояниях, где оно заменяется взаимодействием абсолютно твердых шаров некоторого радиуса r0, так что W(r < r0)=¥. Это приводит к тому, что при столкновении центры молекул не могут сблизиться на расстояние меньшее 2 r0. Если в сосуде имеется N одинаковых молекул, то такую ситуацию можно предстравить как, если бы половина из этих молекvл была заменена неподвижными сферами радиуса 2 r0, а молекулы другой половины были бы точечными и двигались с удвоенной кинетической энергией. Тогда мы бы имели идеальный газ, состоящий из N/2 молекул, находящийся в объеме V-b. Величина b и есть искомая поправка. Уравнение состояния одного моля такого газа можно записать в виде:
|
|
|

Где суммарный недоступный объем газа:

Вторая поправка связана с притягивающим взаимодействием молекул на больших расстояниях, которое приводит к появлению так называемого внутреннего давления газа Р'. Можно показать, что величина Р' будет пропорциональна квадрату концентрации молекул газа (чем больше Молекул газа в объеме, тем больше суммарная сила «самопритяжения»). Поэтому уравнение состояния моля такого газа можно записать в виде:

где a - вторая поправочная величина, представляющая собой некоторую константу, характерную для данного газа.
Объединяя формулы (1.3) 11 (1.5), получим уравнение состояния газа Ван-дер-Ваальса:

Определить зависимость внутренней энергии газа Ван-дер-Ваальса от объема и температуры можно на основании соотношения для газа в состоянии термодинамического равновесия:
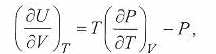
откуда с учетом (1.6) поучим:

Для внутренней энергии неидеального газа получим

Используем выражения (1.1) и (1,8) для определения константы Ван-дер-Вальса для воздуха:

Группируя слагаемые в последнем выражении, получим:

где n = r2 V2 /m - количество молей Воздуха в объеме V2, V1 - объем того же количества молей v воздуха после перетекания через пористую перегородку. Пренебрегая вторыми слагаемыми в квадратных скобках, получим:
 , где Сv =20.786 Дж/(моль×°К)
, где Сv =20.786 Дж/(моль×°К)
зная, что

и проведя не сложные алгебраические преобразования получим:

|
|
|



