Параболическая и полиномиальная регрессии.

Лабораторная работа

Прогнозирование экономических процессов
с помощью табличного процессора Excel.

Требования к содержанию, оформлению и порядку выполнения

Для выполнения лабораторной работы необходимо создать новую рабочую книгу Excel под именем «Ваша фамилия, Лабораторная работа №1, Вариант №_» (например: «Иванов И.П. Лабораторная работа №1»Вариант №4).

Перед выполнением лабораторной работы изучите теоретическую часть и методику выполнения заданий.

Задания необходимо выполнить и оформить согласно своему варианту. Рабочие листы рабочей книги должны быть именованы Задание1, Задание2. Результаты выполнения заданий занести в файл отчета.

Варианты лабораторной работы распределяются согласно номеру № в списке группы см. таблицу

№

Вар.

№

Вар.

№

Вар.

№

Вар.

№

Вар.

№

Вар.

№

Вар.

После выполнения лабораторной работы ответьте на контрольные вопросы. Ответы на контрольные вопросы поместите в файл отчета. Свою рабочую книгу вместе с файлом отчета, необходимо предоставить преподавателю на дискете, подписав ее «Отчет по лабораторной работе №2 студента Иванова И.П., гр. 170404».

Теоретическая часть

Прогнозирование - это метод научного исследования, ставящей своей целью предусмотреть возможные варианты тех процессов и явлений, которые выбраны в качестве предмета анализа.

Задачами экономического прогнозирования являются: предвидение возможного распределения ресурсов по различным направлениям; опреде­ление нижних и верхних границ получаемых результатов; оценка макси­мально возможного количества ресурсов, необходимого для решения хо­зяйственных и научно-технических проблем и др.

В зависимости от периода времени, на которой составляется прогноз (периода упреждения), прогнозы бывает:

· краткосрочные;

· среднесрочные;

· долгосрочные;

· дальнесрочные.

Временная градация прогнозов является относительной и зависит от характера и цели данного прогноза.

Для выполнения краткосрочного прогноза чаще всего применяется метод экстраполяции.

Метод экстраполяции заключается в нахождении значений, лежащих за пределами данного статистического ряда: по известным значениям статистического ряда находятся другие значения, лежащие за пределами этого ряда.

При экстраполяции переносится выводы, сделанные при изучении тенденций развития явления в прошлом и настоящем, на будущее, т.е. в основе экстраполяции лежит предположение об определенной стабильности факторных признаков, влияющих на развитие данного явления.

Рис.1. Основные обозначения метода экстраполяции.

При экстраполяции (см. рис.1.) используется следующая терминология:

t₁ – глубина ретроспекции;

t₂ – момент прогнозирования;

t₃ – прогнозный горизонт;

t₂ – t₁ – интервал наблюдения (промежуток времени, на базе которого исследуется история развития объекта прогнозирования);

t₃ – t₂ – интервал упреждения (промежуток времени на который разрабатывается прогноз).

Чем более устойчивый характер носит прогнозируемые процессы и тенденции, тем дальше может быть отодвинут горизонт прогнозирования. Как показывает практика, интервал наблюдения должен быть в три и более раз длиннее интервала упреждения. Как правило, этот период – довольно короткий. Метод экстраполирования не работает при скачкообразных процессах.

Метод экстраполяции легко реализуется на персональном компьютере. Использование современных табличных процессоров, таких как MS Excel позволяет оперативно проводить прогнозирование экономических процессов с использованием экстраполяционного метода.

Для повышения точности прогноза, необходимо учитывать зависимость прогнозируемой величины Y, от внешних факторов Х. Совокупность изучаемых величин подвержена, как правило, воздействию случайных факторов. В связи с этим зависимость прогнозируемой величины Y, от внешних факторов Х чаще всего статистическая, или – корреляционная.

Статистической называется зависимость случайных величин, при которой каждому значению одной их них соответствует закон распределения другой, то есть изменение одной из величин влечет изменение распределения другой.

Корреляционной называется статистическая зависимость случайных величин, при которой изменение одной из величин влечет изменение среднего значения другой.

Мерой корреляционной зависимости двух случайных величин Х и Y служит коэффициент корреляции r, который является безразмерной величиной, и поэтому он не зависит от выбора единиц измерения изучаемых величин.

Свойства коэффициента корреляции:

1) Если две случайные величины Х и Y независимы, то их коэффициент корреляции равен нулю, т.е. r=0.

2) Модуль коэффициента корреляции не превышает единицы, т.е. |r|£1, что эквивалентно двойному неравенству: -1£r£1.

3) Равенство коэффици­ента -1 или +1 показывает наличие функциональной (прямой) свя­зи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «-» - на связь обратную (увеличение или уменьшение одного признака сопро­вождается противоположным по направлению изменением другого признака).

После определения наиболее существенных факторных признаков влияющих прогнозируемую величину, не менее важно установить их математическое описание (уравнение), дающее возможность численно оценивать результативный показатель через факторные признаки.

Уравнение, выражающее изменение средней величины результативного показателя в зависимости от значений факторных признаков, называется уравнение регрессии.

Линии на координатной плоскости, соответствующие уравнениям регрессии называются линиями регрессии.

Корреляционные зависимости могут выражаться уравнениями регрессии различных видов: линейной, параболической, гиперболической, показательной и т.д.

Линейная регрессия

Уравнением линейной регрессии (выборочным) Y на Х называется зависимость от наблюдаемых значений величины Х, выраженная линейной функцией:

, (1)

где величина r называется коэффициентом линейной регрессии Y на Х, b - константа.

Линейная аппроксимация хорошо описывает изменение величин, происходящее с постоянной скоростью.

Если коэффициент корреляции двух величин Х и Y равен r =±1, то эти величины связаны линейной зависимостью. Коэффициент корреляции служит мерой силы (тесноты) линейной зависимости измеряемых величин. На практике, если коэффициент корреляции двух величин Х и Y |r |>0.5, то считают, что есть основания предполагать наличие линейной зависимости между этими величинами. Однако ориентироваться при выборе типа линии регрессии (линейной или нелинейной) лучше по виду эмпирической зависимости величин Х и Y.

Параболическая и полиномиальная регрессии.

Параболической зависимостью величины Y от величины Х называется зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):

. (2)

Это уравнение называется уравнением параболической регрессии Y на Х. Параметры а, b, с называются коэффициентами параболической регрессии. Вычисление коэффициентов параболической регрессии всегда громоздко, поэтому для расчетов рекомендуется использовать компьютер.

Уравнение (2) параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальной зависимостью величины Y от величины Х называется зависимость, выраженная полиномом n -ого порядка:

, (3)

где числа а_i (i =0,1,…, n) называются коэффициентами полиномиальной регрессии.

Полиномиальная аппроксимация используется для описания величин, попеременно возрастающих и убывающих. Она полезна, например, для анализа большого набора данных о нестабильной величине.

Степенная регрессия.

Степенной зависимостью величины Y от величины Х называется зависимость вида:

. (4)

Это уравнение называется уравнением степенной регрессии Y на Х. Параметры а и b называются коэффициентами степенной регрессии.

Степенная аппроксимация полезна для описания монотонно возрастающей либо монотонно убывающей величины, например расстояния, пройденного разгоняющимся автомобилем. Использование степенной аппроксимации невозможно, если данные содержат нулевые или отрицательные значения.

Показательная регрессия.

Показательной (или экспоненциальной) зависимостью величины Y от величины Х называется зависимость вида:

(или ). (5)

Это уравнение называется уравнением показательной (или экспоненциальной) регрессии Y на Х. Параметры а (или k) и b называются коэффициентами показательной (или экспоненциальной) регрессии.

Экспоненциальная аппроксимация полезна в том случае, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, этот вид приближения неприменим.

Логарифмическая регрессия.

Логарифмической зависимостью величины Y от величины Х называется зависимость вида:

(6)

Это уравнение называется уравнением логарифмической регрессии Y на Х. Параметры а и b называются коэффициентами логарифмической регрессии.

Логарифмическая аппроксимация полезна для описания величины, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Логарифмическая аппроксимация использует как отрицательные, так и положительные величины.

Гиперболическая регрессия.

Гиперболической зависимостью величины Y от величины Х называется зависимость вида:

. (7)

Это уравнение называется уравнением гиперболической регрессии Y на Х. Параметры а и b называются коэффициентами гиперболической регрессии.

 

Качество построения уравнений регрессии характеризует средняя ошибка аппроксимации или относительная ошибка прогноза:

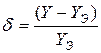(8)

где Y_э – эмпирическое значение прогнозируемого показателя; Y – расчетное значение прогнозируемого показателя.

Проведение регрессионного анализа можно разделить на три этапа: выбор формы зависимости (вида уравнения) на основе статистических данных, вычисление коэффициентов выбранного уравнения, оценка достоверности выбранного уравнения.

Использование табличного процессора позволяет легко выполнить все этапы регрессионного анализа.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: