 |
Линейная зависимость векторов. Базис.
|
|
|
|
Скалярное произведение векторов
Опр.1 Скалярным произведением двух ненулевых геометрических векторов называется число  (или
(или  ), где
), где  угол между векторами
угол между векторами
Свойства скалярного произведения:
1) 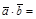
 ; (док. сам.);
; (док. сам.);
2) 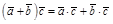 ; (док. сам.);
; (док. сам.);
3)  ; (док. сам.);
; (док. сам.);
4)  , если
, если  – острый,
– острый, 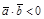 , если
, если  – тупой;
– тупой;
5)  - условие перпендикулярности. ненулевых векторов;
- условие перпендикулярности. ненулевых векторов;
6)  (скалярный квадрат);
(скалярный квадрат);
7) 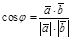 .
.
ПР. Вычислить 
 , если
, если  .
.
Вычисление скалярного произведения через координаты
Пусть 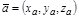 ,
,  . Учитывая свойства скалярного произведения и то, что
. Учитывая свойства скалярного произведения и то, что  ,
, 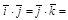
 , получим:
, получим:
 =
=  .
.
Физический смысл скалярного произведения.
Пусть материальная точка перемещается из положения А в положение В под действием силы  Тогда работа, совершаемая при этом,
Тогда работа, совершаемая при этом,  , где
, где  .
.
ПР. Даны точки  . Найти
. Найти  .
. 
Векторное произведение векторов.
Опр.1. Векторным произведением вектора 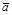 на вектор
на вектор 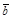 называется вектор
называется вектор  такой, что:
такой, что:
1)  ,
,
2)  ,
,
3) тройка векторов 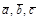 является правой.
является правой.
Свойства векторного произведения:
1) 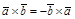 ;
;
2)  ;
;
3) 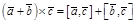 ;
;
4)  - площадь параллелограмма, построенного на векторах
- площадь параллелограмма, построенного на векторах  ;
;
5) если  , то
, то 
ПР. Вычислить  , если
, если  .
. 
Вычисление векторного произведения через координаты
Пусть 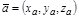 ,
,  ; учитывая, что
; учитывая, что 
 и т.д., получим:
и т.д., получим:
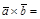
 =…=
=…=  . Физический смысл векторного произведения
. Физический смысл векторного произведения
 − момент силы
− момент силы  , приложенной к точке О.
, приложенной к точке О.
ПР. Найти площадь 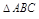 с вершинами
с вершинами 
 .
. 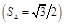
Смешанное произведение векторов
Опр.1. Смешанным произведением упорядоченной тройки векторов  называется число, равное скалярному произведению. вектора
называется число, равное скалярному произведению. вектора  на вектор
на вектор  ; обозначается:
; обозначается:

 .
.
Свойства смешанного произведения:
1)  - объем параллелепипеда, построенного на векторах
- объем параллелепипеда, построенного на векторах  (док. сам.);
(док. сам.);
2) векторы  лежат в одной плоскости (компланарные)
лежат в одной плоскости (компланарные)  если
если  (док. сам.);
(док. сам.);
3)  ;
;
4)  .
.
Вычисление смешанного произведения через координаты
|
|
|
Пусть  ,
,  ,
,  , тогда
, тогда 
 . Док-во:
. Док-во:
ПР. Будут ли векторы  компланарны? Если – нет, найти объем пирамиды, построенной на этих векторах.
компланарны? Если – нет, найти объем пирамиды, построенной на этих векторах. 
§6. n - мерные векторы. Основные понятия.
Опр.1. Вектором называется упорядоченный набор из n действительных чисел:  , где
, где  - называется i – й координатой вектора x,
- называется i – й координатой вектора x,  , или компонентой.
, или компонентой.
Опр.2. Размерностью вектора называется число его координат.
Очевидно, что вектор – это матрица размера  или
или  . Поэтому линейные операции над векторами и их свойства аналогичны линейным операциям над матрицами.
. Поэтому линейные операции над векторами и их свойства аналогичны линейным операциям над матрицами.
Опр.3. Скалярным произведением векторов  и
и  называется число
называется число  .
.
Свойства скалярного произведения:
1) 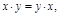 2)
2) 
3)  4)
4)  , причем
, причем 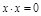 при
при  .
.
Опр. 4. Скалярным квадратом вектора x называется число
 .
.
Опр.5. Число  называется модулем или длиной вектора.
называется модулем или длиной вектора.
Пр.  .
.
Опр.6. Векторы x и y называются ортогональными, если их скалярное произведение равно нулю.
Пр. 
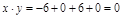 .
.
Опр.7. Некоторое множество V наз. линейным пространством, если:
1) 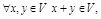 2)
2) 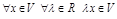 ,
,
причем эти операции обладают свойствами линейных операций.
Очевидно, что множество всех n- мерных векторов образуют линейное пространство (при фиксированном n). Назовем его векторным пространством и обозначим  . В частности,
. В частности,  .
.
Линейная зависимость векторов. Базис.
Опр.1. Линейной комбинацией векторов  называется выражение вида
называется выражение вида  , где
, где  .
.
Пр. 

Опр.2. Система векторов называется линейно зависимой, если из этих векторов можно составить нулевую линейную комбинацию, т.е. 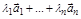 =0, где хотя бы один из коэффициентов
=0, где хотя бы один из коэффициентов  .
.
Теорема 2. (Критерий линейной зависимости системы векторов.) Система векторов линейно зависима тогда и только тогда, когда хотя бы один из ее векторов можно представить в виде линейной комбинации остальных (док. сам.).
Опр.3. Система векторов называется линейно независимой, если из этих векторов невозможно составить нулевую линейную комбинацию, в которой хотя бы один из коэффициентов был отличен от нуля. Т.е. система векторов 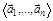 линейно независима, если
линейно независима, если
|
|
|
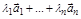 =0
=0  .
.
Утверждение 1. На плоскости любые три вектора являются линейно зависимыми.
Действительно, рассмотрим три ненулевых вектора 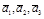 .
.
а) Если  коллинеарны,
коллинеарны, 
 векторы линейно зависимы.
векторы линейно зависимы.
б) Если 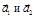 не коллинеарны, то
не коллинеарны, то 


 векторы линейно зависимы.
векторы линейно зависимы.
Опр.4. Векторное пространство называется n-мерным, если в нем существует ровно n линейно независимых векторов, а любая система из (n+1) вектора является линейно зависимой.
Пр. Система векторов 
 …,
…, 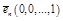 является линейно независимой.
является линейно независимой.
Утверждение 2. Пространство n- мерных векторов является n -мерным. (Без. док-ва.).
Опр.5. Базисом n -мерного пространства называется любая упорядоченная система из n линейно независимых векторов.
ПР. Векторы  образуют базис в пространстве
образуют базис в пространстве  .
.
Теорема 3. (О разложении вектора по базису.)
Если в векторном пространстве выбран базис, то любой вектор этого пространства может быть представлен единственным образом в виде линейной комбинации векторов базиса. (Такое представление называется разложением вектора по базису.)
Теорема 4. (О разложении вектора по базису на плоскости.)
Пусть  – пере неколлинеарных векторов на плоскости. Тогда всякий компланарный им вектор единственным образом можно представить в виде линейной комбинации этих векторов.
– пере неколлинеарных векторов на плоскости. Тогда всякий компланарный им вектор единственным образом можно представить в виде линейной комбинации этих векторов.
Теорема 5. (О разложении вектора по базису в  ). (док. сам.)
). (док. сам.)
Пусть  − три некомпланарных вектора. Тогда любой вектор единственным образом раскладывается в линейную комбинацию этих векторов.
− три некомпланарных вектора. Тогда любой вектор единственным образом раскладывается в линейную комбинацию этих векторов.
Пр. Пусть 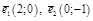 − базис в
− базис в  . Найдем разложение вектора
. Найдем разложение вектора  по этому базису.
по этому базису.
Решение.
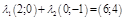

 .
.
Пр. Будут ли векторы  образовывать базис в пространстве? Если да, то найти разложение вектора
образовывать базис в пространстве? Если да, то найти разложение вектора  по этому базису.
по этому базису.
Решение.
Предположим, что  . Тогда
. Тогда

 , а векторы
, а векторы 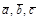 образуют базис.
образуют базис.


Следовательно,  .
.
|
|
|


