 |
Выполнение сопряжений с помощью ЭВМ и графического редактора AutoCAD.
|
|
|
|
Оформление машиностроительного чертежа.
Сопряжения.
Методические указания к выполнению практических работ по
дисциплине “Инженерная и графика”
Ростов-на-Дону
| Составители: | канд. техн. наук, профессор М.В.Савенков доцент А.И.Ананченко, канд.техн.наук доц. С.А.Гришин, ассистент О.А.Пятницкая. |
УДК 004.92
Оформление машиностроительного чертежа. Сопряжения: Метод. указания к выполнению практических работ по дисциплине “Инженерная графика”. - Ростов-на-Дону, Издательский центр ДГТУ, 2010. 29с.
Методические указания предназначены для студентов младших курсов, изучающих дисциплину “Инженерная графика“. В них рассматриваются основные ГОСТы по оформлению машиностроительного чертежа.
А также методика построения сопряжений использующихся при выполнении контура сложных деталей состоящих из прямолинейных участков и кривых второго порядка.
Печатается по решению методической
комиссии конструкторского факультета
Научный редактор: докт.техн.наук, проф. Г.А. Кузин
Рецензент: зав.каф. графики РГАСМ профессор Д.Н.Бородин
© Издательский центр ДГТУ, 2010
Введение
Графические изображения (чертежи) имеют широкое применение в самых разнообразных сферах человеческой деятельности. Особенно велика роль чертежа в науке и технике. Ни одна современная машина, ни одно инженерное сооружение не могут быть построены без чертежей.
Чертеж не без основания называют «языком техники», а потому без знаний, приобретенных в курсе черчения, в котором изучается этот «язык», невозможна инженерная деятельность человека.
Чертежи изделий или сооружений могут быть изготовлены как по готовым образцам, так и путем проектирования. Для этого инженер должен иметь комплекс определенных знаний в данной области, хорошо развитое пространственное мышление и умение выполнять графические построения.
|
|
|
Изучение курса инженерной графики преследует следующие цели:
1. Обучение способам изображения различных предметов на плоскости в прямоугольных и аксонометрических проекциях (выполнение чертежей);
2. Приобретение навыков пространственных форм машин, узлов, деталей и т.п., изображаемых на чертежах (чтение чертежей).
Выполнять чертежи следует только после предварительного изучения соответствующих учебных материалов.
Особое внимание нужно уделить изучению государственных стандартов (ГОСТ), относящихся к правилам выполнения чертежей.
ОФОРМЛЕНИЕ ТЕХНИЧЕСКИХ ЧЕРТЕЖЕЙ И ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ
ГОСТ 2.301-68 - ФОРМАТЫ ЧЕРТЕЖЕЙ
ГОСТ 2.301-68 устанавливает основные и дополнительные форматы листов чертежей и других документов, предусмотренных стандартами на конструкторскую документацию всех отраслей промышленности и строительства.
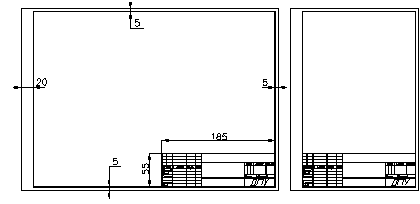
Форматы листов определяются размерами внешней рамки (выполненной тонкой линией) оригиналов, подлинников, дубликатов, копий.
За основные форматы принимаются формат с размерами сторон 1189x841 мм, площадь которого равна 1 м2, и другие форматы, полученные путем последовательного деления его на две равные части параллельно меньшей стороне соответствующего формата. Основные форматы: А0- 841x189; А1- 594х841; А2- 420х594; А3- 297х420;
А4- 210х297.
|
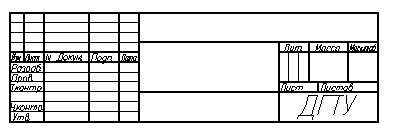
Конструкторский документ должен иметь основную надпись, форма и размер которой установлены ГОСТ 2.104-68. Для чертежей и схем установлена форма 1 основной надписи, которая приведена ниже на рисунке.
|
Допускается применение дополнительных форматов, образуемых увеличением коротких сторон форматов на величину, кратную их размерам. Дополнительные форматы: А0х2- 1189x1682; А0хЗ- 1189x2523;
|
|
|
А1хЗ- 841х1783; А1х4- 841х2378; А2хЗ- 504х1261; А2х4- 594х1682;
А2х5- 594x2102; АЗхЗ- 420х891; А3х4- 420х1189; А3х5- 420х1486;
А3х6- 420х1783; А3х7- 420х2080; А4хЗ- 297х630; А4х4- 297х841;
А4х5- 297х1051; А4х6- 297х1261; А4х7- 297х1471; А4х8- 297х1682;
А4х9- 297Х1892.
ГОСТ 2.302-68 - МАСШТАБЫ
Масштабом называется отношение чисел, показывающее, во сколько раз изображение предмета на чертеже увеличено или уменьшено по отношению к своим действительным размерам. В зависимости от сложности и величины изображения масштабы на чертежах должны выбираться из следующего ряда:
Масштабы уменьшения: 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000
Натуральная величина: 1:1
Масштабы увеличения: 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1
ГОСТ 2.303-68 - ЛИНИИ
ГОСТ 2.303-68 устанавливает начертания и основные назначения линий на чертежах всех отраслей промышленности и строительства.
| Наименование | Начертание | Толщина Линии | Основное назначение |
| Сплошная основная | S(0,5-1,4) | Линии видимого контура. Линии перехода видимые. Линии контура сечения (вынесенного или входящего в состав разреза). | |

|
| Наименование | Начертание | Толщина Линии | Основное назначение |
| Сплошная тонкая |

| S/3 – S/2 | Линии контура наложенного сечения. Линии размерные и выносные. Линии штриховки. Линии выноски. Полки линий-выносок и подчеркивание надписей. Линии для изображения пограничных деталей (обстановка). Линии ограничения выносных элементов на видах, разрезах и сечениях. Линии перехода воображаемые. Следы плоскостей, линии построения характерных точек при специальных построениях (линии связи) |
| Сплошная волнистая | 
| S/3 – S/2 | Линии обрыва. Линии разграничения вида и разреза. |
| Штриховая | 
| S/3 – S/2 | Линии невидимого контура. Линии перехода невидимые. Длину штрихов следует выбирать в пределах 2-8 мм, а расстояние между штрихами 1-2 мм. |
| Штрих пунктирная тонкая | 
| S/3 – S/2 | Линии осевые и центровые. Линии сечений, являющиеся осями симметрии для наложенных или вынесенных сечений. Длину штрихов следует выбирать в пределах 5-30 мм, а расстояние между штрихами 3-5 мм. Центры окружностей во всех случаях выполняют пересечением штрихов, а не точкой. |
|
|
|
| Наименование | Начертание | Толщина Линии | Основное назначение |
| Штрих пунктирная толстая | 
| S/2 – S | Линии, обозначающие поверхности, подлежащие термообработке или покрытию. Линии для изображения элементов, расположенных перед секущей плоскостью (наложенная поверхность). |
| Штрих пунктирная с 2-мя точками | 
| S/3 – S/2 | Линии сгиба на развертках. Линии для изображения частей изделий в крайних или промежуточных положениях. Линии для изображения развертки, совмещенной с видом. |
| Сплошная тонкая с изломами | 
| S/3 – S/2 | Длинные линии обрыва. |
| Разомкнутая | 
| S – 1,5S | Линии сечений. Длина штрихов выбирается в пределах 8-20 мм. |
ГОСТ 2.304-81 – ШРИФТЫ ЧЕРТЕЖНЫЕ
Шрифты, которыми выполняют надписи на чертежах, установлены ГОСТ 2.304-81. Различают следующие шрифты: а) основной и широкий; б) шрифт с наклоном и без наклона. Наиболее часто на чертежах применяют шрифт основной с наклоном 75°. Этим шрифтом выполняются все надписи на чертежах. Размер шрифта h определяется высотой прописных букв, мм: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.
Типы шрифтов:
тип А без наклона (толщина линий шрифта d=T/14h);
тип А с наклоном около 75° (d=l/14h);
тип Б без наклона (d=1/10h);
тип Б с наклоном около 75° (d=l/10h).
Таблица. Параметры шрифтов
| Параметры | Размеры, мм. Шрифт типа А | ||||||
| h c a b e d | 2,5 1,8 0,35 4,0 1,1 0,18 | 3,5 2,5 0,5 5,5 1,5 0,25 | 5,0 3,5 0,7 8,0 2,1 0,35 | 7,0 5,0 1,0 11,0 3,0 0,5 | 10,0 7,0 1,4 16,0 4,2 0,7 | 14,0 10,0 2,0 22,0 6,0 1,0 | 20,0 14,0 2,8 31,0 8,4 1,4 |
| Шрифт типа Б | |||||||
| h c a b e d | 2,5 1,8 0,35 4,3 1,5 0,25 | 3,5 2,5 0,7 6,0 2,1 0,35 | 5,0 3.5 1,0 8,5 3,0 0,35 | 7,0 5,0 1,4 12,0 4,2 0,7 | 10,0 7,0 2,0 17,0 6,0 1,0 | 14,0 10,0 2,8 24,0 8,4 1,4 | 20,0 14,0 4,0 34,0 12,0 2,0 |
Примечания:
1. Обозначения: h — размер шрифта; с — высота строчных букв;
a — расстояние между буквами; b — минимальный шаг строк;
e — минимальное расстояние между словами; d — толщина линий шрифта.
2. Относительные размеры параметров шрифта:
| Параметры | Тип А | Тип Б |
| h | (14/14)h = 14d | (10/10)h.= 10d |
| c | (10/14)h = 10d | (7/10)h = 7d |
| a | (2/14)h = 2d | (2/10)h = 2d |
| E | (22/14)h = 22d | (17/10)h =17d |
| b | (6/14)h = 6d | (6/10)h = 6d |
| d | (1/14)h = d | (1/10)h = d |
|
|
|

СОПРЯЖЕНИЯ
Плавные переходы от одной прямой или кривой линии к другой называются сопряжениями и выполняются преимущественно на основе свойств прямых, касательных к окружностям, или касающихся между собой окружностей. Дуги окружностей, при помощи которых выполняется сопряжение, называются дугами сопряжения. Для построения дуги сопряжения необходимо вы явить ее центр, радиус этой дуги и точки сопряжения.
| Графическое построение сопряжений | |
| 1. Сопряжение пересекающихся прямых с помощью дуги заданного радиуса R. | |

| |
| Провести прямые, параллельные сторонам угла на расстоянии R. Из точки О взаимного пересечения этих прямых, опустив перпендикуляры на стороны угла, получим точки сопряжения 1 и 2. Радиусом R провести дугу. |
| 2. Сопряжение дуги окружности и прямой с помощью дуги заданного радиуса R. | |

| |
| На расстоянии R провести прямую, параллельную заданной прямой, а из центра О1 радиусом R+R1 – дугу окружности. Точка О – центр дуги сопряжения. Точку 2 получим на перпендикуляре, проведенном из точки О на заданную прямую, а точку 1 – на прямой ОО1. |
| 3. Сопряжение дуг двух окружностей радиусов R1 и R2 прямой линией. | |

| Из точки O1 провести окружность радиусом R1 — R2. Отрезок O1O2 разделить пополам и из точки 03 провести дугу радиусом 0,5 0102. Соединить точки O1 и О2 с точкой А. Провести прямую параллельную А02. Она касается окружностей R и R Из точки 02 провести перпендикуляр к прямой АО2. Точки 1,2 — точки сопряжения. |
| 4. Сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (внешнее сопряжение). | |

| Из центров O1 и 02 провести дуги радиусов R1+R и R2+R. Получаем точку О — центр дуги сопряжения. Соединить точки O1 и 02 с точкой О. Точки 1 и 2 являются точками сопряжения. |
| 5. Сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (внутреннее сопряжение). | |

| Из центров О1 и О2 провести дуги радиусов R-R1, и R-R2. Получаем точку О – центр дуги сопряжения. Соединить точки О1 и О2 с точкой О до пересечения с заданными окружностями. Точки 1 и 2 – точки сопряжения. |
| 6. Сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (смешанное сопряжение). | |

| Из центров О1 и О2 соответственно провести дуги радиусов R3=R+R1 и R4=R+R2. Получаем точку О – центр дуги сопряжения. Соединить точки О1 и О2 с точкой О до пересечения с заданными окружностями. Точки 1 и 2 – точки сопряжения. |
ЛЕКАЛЬНЫЕ КРИВЫЕ
Лекальные кривые – это не циркульные кривые линии, которые вычерчиваются по точкам с помощью лекал (вручную на бумаге) или построенные по определенному закону на компьютере. Алгебраические кривые линии, имеющие в системе декартовых координат уравнения второй степени, называют кривыми второго порядка. К лекальным кривым второго порядка относятся: эллипс, парабола, гипербола.
|
|
|
ЭЛЛИПСОМ называется (плоская замкнутая) кривая, состоящая из множества точек, сумма расстояний от каждой точки которой до двух данных точек - фокусов, величина постоянная. Расстояние между фокусами называется фокусным. Точка пересечения осей симметрии эллипса называется центром, а точка пересечения осей с эллипсом - его вершинами. Отрезки, которые соединяют противоположные вершины, называются соответственно большой и малой его осями. Чтобы графически определить положение фокусов, расположенных на большой оси, из вершины малой оси осуществляют засечки радиусом, равным величине половины большой оси. Отрезки, которые соединяют фокусы эллипса с точкой кривой, называются радиус-векторами, а угол между радиус-векторами – фокальным углом. Чтобы определить направление касательной в произвольной точке эллипса, строят радиус-векторы, затем проводят биссектрису фокального угла, перпендикуляр к которой является касательной к образующей эллипса в точке К.

|

| Существует множество способов построения эллипса. Рядом на рисунке приведен один из них наиболее часто применяемый на практике. |
ПАРАБОЛОЙ -называется плоская кривая, все точки которой равно отстоят от данной точки (фокуса F) и от данной прямой (директрисы), лежащих в одной плоскости. Концы параболы удаляются в бесконечность. Вершина параболы равноудалена от фокуса и директрисы.
Способ построения параболы выбирают в зависимости от задающих элементов.
Построение параболы по заданной вершине (А), оси и точки (5) параболы. Из точек А и (5) проводят взаимно перпендикулярные прямые до пересечения их в точке D. Отрезки АD и D5 делят на одинаковое количество равных частей (в данном случае на 5 частей). Через точки деления на AD проводят горизонтальные прямые (параллельные оси АВ), а точки на D5, соединяют с вершиной А. Точки пересечения одноименных вспомогательных прямых будут принадлежать очерку параболы. Полученные точки соединяют плавной кривой, а затем строят симметрично вторую половину параболы.
Чтобы определить на заданной параболе графическим способом расположение ее фокуса и директрисы KN, поступают так:
1. Выбирают на параболе произвольную точку М, затем откладывают от вершины О параболы по оси влево расстояние а и проводят прямую LM, которая является касательной к параболе в точке М.
2. из точки А, в которой проведенная касательная LM пересекает вертикальную линию, проводят перпендикуляр NA к касательной (нормаль

| NAF)и в точке его пересечения с осью получают искомый фокус параболы - точку F. Точка N, принадлежащая директрисе, является точкой пересечения нормали FN с прямой, проведенной через точку М параллельно оси. Точка Е, лежащая на вертикальной линии FE,находится от фокуса на расстоянии EF=FK=p,где р- параметр параболы. |
КИНЕМАТИЧЕСКИЕ КРИВЫЕ
Кинематические кривые получаются в результате движения какой-либо точки по определенному закону. Такие кривые можно определить как траекторию точки, связанной неизменно с некоторой подвижной кривой линией (подвижной центроидой), которая катится без скольжения по неподвижной кривой линии (неподвижной центроиде).
Циклоидальными называются кривые линии, построенные при помощи центроид дуг окружностей. К ним относятся циклоида, эпициклоида, гипоциклоида, эвольвента и др. У циклоиды подвижная центроида – окружность, а неподвижная – прямая линия, которую можно принять за окружность, центр которой несобственная точка.
Обыкновенная циклоида – это плоская кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии. Для ее построения от исходного положения точки А на направляющей прямой откладывают отрезок АА1, равный длине данной окружности 2pR. Окружность и отрезок АА1 делят на одинаковое число равных частей. Восстанавливая перпендикуляры из точек деления прямой АА1 до пересечения с прямой, проходящей через центр данной окружности параллельно АА1, намечают ряд последовательных положений центра перекатываемой окружности О1, О2, О3, …, О12. Описывая из этих центров дуги радиусом R, отмечают точки пересечения с ними прямых, проходящих параллельно АА1 через точки деления окружности 1, 2, 3, 4 и т.д. На пересечении горизонтальной прямой, проходящей через точку 1, с дугой, описанной из центра О1, находится одна из точек циклоиды; на пересечении прямой, проходящей через точку 2, с дугой, проведенной из центра О2, находится другая точка циклоиды и т.д.
Прямая М-7, соединяющая данную точку М с точкой 7 касания перекатываемой окружности с направляющей АА1, является нормалью циклоиды в данной точке; перпендикуляр к М-7 дает касательную. Длина дуги циклоиды АМА1=8R; площадь ограниченная циклоидой и прямой АА1, равняется 3pR2.

|
Эвольвента (развертка) окружности – плоская кривая, которую описывает любая точка прямой линии, катящейся по неподвижной окружности. В этом случае неподвижная центроида – окружность, а подвижная центроида – прямая линия (окружность с центром – несобственной точкой).

| Для построения эвольвенты (развертки окружности) - окружность предварительно делят на произвольное число равных частей. В точках деления проводят касательные к окружности, направленные в одну сторону. На касательной, проведенной через последнюю точку деления, откладывают отрезок, равный длине окружности (2pR), и делят |
его на то же число равных частей. Откладывая на первой касательной одно деление окружности, на второй – два, на третьей – три и т.д., получают ряд точек 11, 21, 31, 41 и т.д., которые соединяют по лекалу. Это и будет эвольвента.
Касательная к эвольвенте, например в точке 71, перпендикулярна к касательной 7-71 окружности.
Синусоида – плоская кривая, графически изображающая изменение синуса в зависимости от изменения его аргумента (угла). Для построения синусоиды исходную окружность делят на произвольное число равных частей. На такое же число равных частей делят отрезок прямой, равный длине данной окружности (2pR). Проведя через одноименные (соответствующие) точки деления горизонтальные и вертикальные прямые, находят на их пересечении точки синусоиды.

|
ВИНТОВЫЕ ЛИНИИ
Цилиндрическая винтовая линия (гелиса) – пространственная кривая, которая образуется в результате сложного движения точки – вращения вокруг оси и поступательного движения вдоль прямой, параллельной этой оси. Шаг винтовой линии – расстояние между двумя ее соседними витками в направлении, параллельном оси винтовой линии. Шаг винтовой линии обозначают буквой Р. Разверткой цилиндрической винтовой линии является прямая. Угол называется углом подъема винтовой линии. Рядом представлен чертеж правой гелисы. Как видно фронтальная проекция гелисы изобразилась синусоидой.

|
Выполнение контура “КУЛАЧОК”
Кулачок – это звено (деталь) кулачкового механизма, профиль которого обеспечивает требуемый закон движения исполнительному звену.
Например, кулачки на распределительном валу двигателя внутреннего сгорания. Пример оформления задания показан на рисунке.

|
Задания для построения очертания кулачка по вариантам приведены ниже.
Варианты 1, 7, 11, 17, 21, 24, 28. Порядок построения:
1. Выбрать положение осей координат ОХ и ОУ, предполагая размещение профиля кулачка в центре поля чертежа.
2. Провести дугу радиуса R - участок АЕ.
3. Построить синусоиду, исходная окружность d1 – участок АВ.
4. Построить половину эллипса с полуосями a и b – участок DC.
5. Построить сопряжение эллипса с дугой радиуса R2 в точке С.
6. Построить сопряжение дуг R1 и R2 дугой R3.
7. Определить положение точки D на образующей эллипса по координате y.
8. Построить касательную к эллипсу в точке D.
9. Определяется центр сопряжения на пересечении нормали окружности в точке Е и биссектрисы угла между касательными. Определяется радиус сопряжения Rx и строится сопряжение этим радиусом.
10. Построить центральное отверстие со шпоночным пазом.
11. Наносятся размерные линии, условные обозначения заменить их численными значениями с соответствующими знаками R, Ø. Знаки и цифры выполняются шрифтом №5 ГОСТ 2.304-81.
12. Обвести контур кулачка основной линией.
ПРИМЕЧАНИЕ: вспомогательные построения проводить тонкими линиями и сохранить их на готовом чертеже.
| Вариант | R | R1 | R2 | R3 | a | b | d | d1 | h | t | x | y |
| 1, 24, 11, 28 |

|
| Вариант | R | R1 | R2 | R3 | a | b | d | d1 | h | t | x | y |
| 7, |

|
Варианты 2, 8, 12, 18, 22, 29. Порядок построения:
1. Выбрать положение осей координат ОХ и ОУ, предполагая размещение профиля кулачка в центре поля чертежа.
2. Построить эллипс с полуосями а и b - участок CD.
3. Провести дугу радиуса R - участок DK.
4. Построить эвольвенту окружности диаметром d1, вьделить пятую и восьмую точки - участок АВ.
5. Построить касательные к эвольвенте в точке В и к дуге радиуса R в точке К; построить сопряжение касательных найденным радиусом Rx - участок КВ.
6. Построить сопряжение эллипса в точке С с дугой радиуса R2 и эвольвенты в точке А с дугой радиуса R1, построить внешнее сопряжение дуг радиусов R1 и R2 дугой радиуса R3 - участок СА.
7. Обвести контур кулачка основной линией.
ПРИМЕЧАНИЕ: вспомогательные построения проводить тонкими линиями и сохранить их на готовом чертеже.
| Вариант | R | R1 | R2 | R3 | a | b | d | d1 | h | t | x | y |
| 2, 22, 12, 29 |

|
| Вариант | R | R1 | R2 | R3 | a | b | d | d1 | h | t | x | y |
| 8, |

|
Варианты 3, 9, 13, 19, 26, 30. Порядок построения:
1. Выбрать положение осей координат ОХ и ОY, предполагая размещение профиля кулачка в центре чертежа.
2. Определить положение центра эллипса, после чего построить его, используя параметры полуосей эллипса a и b.
3. В точке D провести касательную к образующей эллипса.
4. Построить параболу, вершина которой определяется размером S и точками А и В, которые заданны размерами а1 и b1.
5. Провести касательные параболы в точках А и В.
6. Провести дугу радиуса R из центра кулачка.
7. Провести дугу радиуса R1. После чего выполнить построение сопряжения радиусом R2 между касательной параболы, проходящей через точку А, и радиусом R1.
8. Выполнить сопряжение радиусом R3 между точкой С лежащей на эллипсе и дугой радиуса R.
9. Выполнить сопряжение угла радиусом Rx. Для чего находим центр сопряжения на пересечении нормали в точке D эллипса и биссектрисы угла между касательными параболы и эллипса. После чего определяется величина радиуса сопряжения.
10. Обвести контур кулачка основной линией.
ПРИМЕЧАНИЕ: вспомогательные построения проводить тонкими линиями и сохранить их на готовом чертеже.
| Вариант | R | R1 | R2 | R3 | S | a | a1 | b | b1 | D | h | t | x | y |
| 3, 26, 13, 30 |

|
| Вариант | R | R1 | R2 | R3 | S | a | a1 | b | b1 | d | h | t | x | y |
| 9, |

|
Варианты 4, 6, 14, 16, 23, 27. Порядок построения:
1. Выбрать положение осей координат ОХ и ОУ, предполагая размещение профиля кулачка в центре поля чертежа.
2. Провести дугу радиуса R – участок АЕ.
3. Построить циклоиду, подвижная центроида которой окружность диаметром d1 -участок AM.
4. Построить эллипс с полуосями а и Ь, указать точку D. Построить фокальный угол, на биссектрисе фокального угла отметить центр дуги R2 и провести ее.
5. Выполнить сопряжение дуг R1 и R2 дугой R3.
6. Выполнить сопряжение тупого угла радиусом Rx, центр дуги сопряжения находится на пересечении биссектрисы угла с осью ОУ.
7. Строим центральное отверстие со шпоночным пазом.
8. Наносим размерные линии, условные обозначения заменить их численными значениями с соответствующими знаками R, Ø. Знаки и цифры выполняются шрифтом № 5 ГОСТ 2.304-81.
9. Обвести контур кулачка основной линией.
ПРИМЕЧАНИЕ: вспомогательные построения проводить тонкими линиями и сохранить их на готовом чертеже.
| Вариант | R | R1 | R2 | R3 | a | b | d | d1 | h | t | x | y | y1 |
| 4, 27, 14, |

|
| Вариант | R | R1 | R2 | R3 | a | b | d | d1 | h | t | x | y | y1 | |
| 6, | ||||||||||||||

|
Варианты 5, 10, 15, 20, 25. Порядок построения.
11. Выбрать положение осей координат ОХ и ОY, предполагая размещение профиля кулачка в центре чертежа.
12. Провести дугу радиуса R из точки Е (60о).
13. Построить ¼ эллипса участок DE. Из точки D провести касательную (перпендикуляр к биссектрисе фокального угла).
14. Построить параболу на расстоянии S от центра по данным а1 и b1 под углом 30о – участок АВ.
15. Выполнить сопряжение угла радиусом Rx, центр которого находится на пересечении биссектрис тупого угла и фокального угла – участок DA.
16. Построить сопряжение дуг R1 и R2 дугой R3 – участок CЕ.
17. Обвести контур кулачка основной линией.
ПРИМЕЧАНИЕ: вспомогательные построения проводить тонкими линиями и сохранить их на готовом чертеже.
| Вариант | S1 | a1 | b1 | R | a | b | y | y1 | R1 | R2 | R3 | d | h | t |
| 5, 15, 25 | 50,5 |

|
| Вариант | S1 | a1 | b1 | R | a | b | y | y1 | R1 | R2 | R3 | d | h | t |
| 10, |

|
Выполнение сопряжений с помощью ЭВМ и графического редактора AutoCAD.
Выполнение чертежей с помощью компьютера вносит ряд особенностей, которые присущи только компьютерной графике.
Так при выполнении сопряжений сохраняются практически все элементы геометрических построений, которые выполняются с применением циркуля, а в AutoCAD с помощью команды (окружность). Но вместе с тем некоторые кривые второго порядка выполняются иначе. Так выполнение эллипса в AutoCAD производится по команде ELLIPSE. При этом выполнение эллипса может быть выполнено либо сплошной тонкой линией, либо сплошной основной линией. Для выполнения эллипса последней из линий сначала надо задать выполнение элемента эллипс командой AutoCAD “ Polyline ”. Это осуществляется вводом с клавиатуры команды “ Pellipse ” и изменение параметра “ 0 ” на “ 1 ”. После этих действий выполнение эллипса будет осуществляться сплошной толстой линией (Polyline). Однако на чертеже она будет выглядеть в виде тонкой линии. Поэтому в конечном итоге потребуется изменить ее толщину на требуемую, что осуществляется с помощью редактирования линии-“Polyline”. Редактирование команды “Polyline” осуществляется из падающего меню Modify c последующим обращением к опциям Object > Polyline. После активизации команды редактирования осуществляется сначала выделение объекта – эллипса, а затем выбор типа редактирования (в данном случае изменение толщины линии), что осуществляется набором с клавиатуры ключа “ W ” включения команды “Width”, и затем ввода нового значения толщины линии контура эллипса. Аналогичным образом осуществляется изменение толщины линий выполненных с помощью команды -“Polyline” и при построении циклоиды, параболы и синусоиды. Кроме этого с помощью команды редактирования полилинии можно проводить сглаживание ломанных кривых линий. Это возможно при использовании опции “ Spline ”.
При обводке сложных дуг окружностей сопрягаемых друг с другом и имеющих положительную и отрицательную кривизну также используют команду -“Polyline” из падающего меню “Draw”. При этом надо помнить, что выполнение дуги в AutoCAD выполняется против часовой стрелки.
Поэтому для выполнения дуги, как это требует команда -“Polyline” сначала задают начальную точку выполнения первой дуги, затем задают толщину линии. После этого включают выполнение команды “Polyline” по дуге подключая опцию “ Arc ” с помощью вводимого ключа “ A ”. Далее если дуга выполняется не по требуемой траектории, включается опция определения ее центра “ CEnter ” вводом с клавиатуры ключевых букв “ CE ”, а затем проводя обводку сложного контура фиксируя контрольные точки сопряжения, предварительно включив команду объектной привязки.
Литература
1. Государственные стандарты. Указатель 2001. Т.1-4. М.: ИПК изд-во стандартов. 2001 г.
2. ГОСТ 2.301-68 – 2.304-81 – Общие правила выполнения чертежей.
3. Чекмарев А.А. Инженерная графика. – М.: Высшая школа, 2002 г.
4. Левицкий B.C. Машиностроительное черчение и автоматизация выполнения чертежей: Учеб. Для втузов.- 7-е изд., испр, и доп. М.: Высш. школа 2006 г.
5. Попова Г.Н., Алексеев СЮ. Машиностроительное черчение: Справочник. СПБ. Политехника. 2005.
6. Эффективная работа: AutoCAD 2002 / Ш.Тику. – СПб.: Питер, 2003. –1168 с.
7. Финкельштейн Эллен. AutoCAD 2002. Библия пользователя: Пер. с англ. - М.: Издательский дом “Вильямс”, 2003.-1072с.
8. Инженерная графика. Конструкторская информатика в машиностроении: Учеб. для вузов 3-е изд. перераб. и доп. /Болтухин А.К., Васин С.А., Вяткин Г.П., Пуш А.В./ М.: Машиностроение, 2005 г.
|
|
|


