 |
Взаимное положение двух прямых линий
|
|
|
|
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ»
Проекции с числовыми отметками
Методические указания к выполнению задания по начертательной
геометрии и черчению
Набережные Челны
УДК 121.021.(076)
Проекции с числовыми отметками: Методические указания к практическим занятиям по начертательной геометрии / Составители Ахмедова А.А., Рзаева Т.В., Шарафутдинова Р.В.– Наб. Челны: ИНЭКА, 2006. – 24 с.
Печатается в соответствии с решением научно-методического совета Камской государственной инженерно-экономической академии.
Методические указания предназначены в помощь студентам заочного отделения инженерно-строительного факультета. Включает краткое изложение теории по теме «Проекции с числовыми отметками» и необходимый материал для выполнения задания.
Рецензент: к.т.н., доцент кафедры СК Ш.Х. Нетфулов
ПРОЕКЦИИ С ЧИСЛОВЫМИ ОТМЕТКАМИ
СУЩНОСТЬ МЕТОДА. ПРОЕКЦИИ ТОЧЕК
Метод проекций с числовыми отметками находит широкое применение в тех случаях, когда высота изображаемого предмета невелика сравнительно с его длиной и шириной и при изображении поверхности земли.
Сущность метода заключается в том, что предмет проецируется методом ортогонального проецирования только на одну плоскость проекций, которая располагается горизонтально, называется плоскостью нулевого уровня и обозначается П0.
Чтобы по чертежу иметь возможность восстановить положение точки в пространстве, рядом с проекцией каждой точки проставляется цифра – числовая отметка, указывающая в метрах расстояние от точки до плоскости нулевого уровня.
|
|
|
Точки, расположенные над плоскостью нулевого уровня, имеют положительные отметки, точки, расположенные ниже плоскости, имеют отрицательные отметки, точки, лежащие в плоскости, имеют нулевую отметку.
Рисунок 1
На рисунке 1 наглядно показано построение проекций точек. Числовые отметки, проставленные у точек А, В, С показывают, что точка А находится над плоскостью П0 на высоте 6 м. Точка В расположена под плоскостью П0 на расстоянии 5 м. А точка С лежит в плоскости нулевого уровня.
Рисунок 2
Изображение этих трех точек в проекциях с числовыми отметками дано на рисунке 2.
Обычно расстояние точек от плоскости нулевого уровня выражается в тех же единицах масштаба, в которых измеряются расстояния на этой плоскости.
ПРОЕКЦИИ ПРЯМЫХ ЛИНИЙ
Прямая линия в проекциях с числовыми отметками изображается проекцией на П0 и отметками двух точек.
Условимся называть длину проекции отрезка прямой заложением прямой и обозначать L (см. рисунок 3).
Разность высот концов отрезка назовем превышением и обозначим J
hB – hA =J
Рисунок 3
Заложение прямой, соответствующее единице превышения, называется интервалом прямой и обозначается 
.
Интервал численно равен отношению заложения к превышению
;
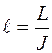Величина превышения, приходящаяся на заложение, равной единице называется уклоном i.
; 
где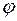 
- есть угол наклона прямой к плоскости.
Проградуировав проекцию прямой, можно графически определить интервал прямой.
Проградуировать проекцию прямой – значит определить на ней точки с постоянной разностью отметок, равной единице.
На рисунке 4 показано графическое градуирование проекции отрезка АВ методом пропорционального деления.
Рисунок 4
Через точку А произвольно проведен отрезок прямой АК, на котором отложены произвольные равные отрезки А3 40 , 40 50 , 50 60 , 60 70.
|
|
|
Прямые, проведенные из точек 40, 50,60 параллельно прямой 70 В определяют в пересечении с проекцией прямой искомые точки 4, 5, 6.
Горизонтальная прямая проецируется на плоскость нулевого уровня в прямую, имеющую одинаковые числовые отметки двух точек рисунок 5 (рисунок 5).
Вертикальная прямая проецируется на плоскость нулевого
уровня в точку, имеющую числовые отметки двух точек (рисунок 5).
Взаимное положение двух прямых линий
Две прямые линии в пространстве могут пересекаться, быть взаимно параллельными или скрещиваться.
Рисунок 6 Рисунок 7
Если две прямые пересекаются, то проекция пересекаются в точке, которая будучи отнесена к каждой из пересекающихся прямых имеет одинаковую отметку (рисунок 6).
Следствие: любые две горизонтальные линии, имеющие одинаковые отметки и не параллельные друг другу, взаимно пересекаются (рисунок 7)
Если две прямые взаимно параллельны, интервалы равны и отметки возрастают в одну сторону (рисунок 8).
Рисунок 8
Если проекции прямых не удовлетворяют условиям взаимного пересекания или параллельности, то, очевидно, что это проекции скрещивающихся прямых.
ПРОЕКЦИИ ПЛОСКОСТЕЙ
Проекции плоскостей
В проекциях с числовыми отметками можно задать плоскость теми же определителями, как и в ортогональных проекциях, а именно: проекциями трех точек, не лежащих на одной прямой (рисунок 9), проекциями прямой и точки вне прямой (рисунок 10), проекциями двух параллельных прямых (рисунок 11), двух пересекающихся прямых (рисунок 12), или проекцией плоской фигуры (рисунок 13).
Но обычно в проекциях с числовыми отметками плоскость задается так называемым масштабом уклонов.
На рисунке 14 изображена плоскость Σ, пересекающая плоскость нулевого уровня по следу Σno. В плоскости Σ проведена линия наибольшего ската и построена ее проекция на плоскость проекций П0.
Рисунок 9
Рисунок 10 Рисунок 11
Рисунок 12 Рисунок 13
Рисунок 14
Угол 
между линией наибольшего ската к ее проекцией есть угол наклона плоскости Σ к плоскости проекций.
|
|
|
Пересечем плоскость Σ горизонтальными плоскостями, отстоящими друг от друга на одну единицу высоты.
Линии пересечения этих плоскостей с плоскостью Σ, являясь горизонталями плоскости Σ, будут параллельны следу Σ По и перпендикулярны линии наибольшего ската.
Проекции этих горизонталей тоже параллельны следу Σ По и перпендикулярны проекции линии наибольшего ската.
Так как секущие плоскости расположены через единицу, то расстояние между проекциями горизонталей будет равно интервалу линии наибольшего ската данной плоскости.
Проекции линии наибольшего ската плоскости с нанесенными на ней интервалами называется масштабом уклонов плоскости.
Масштаб уклонов плоскости принято вычерчивать в виде двух параллельных прямых, одна из которых проводится несколько толще другой, с нанесенными перпендикулярно к ним отрезками горизонталей данной плоскости и обозначается (рисунок 15).
Расстояние между проекциями смежных горизонталей называется интервалом плоскости. Из построений, приведенных на рисунке 14, видно, что интервал
Рисунок 15 плоскости равен
интервалу линии
наибольшего ската ее.
Задание плоскости в проекциях с числовыми отметками является наиболее удобным способом задания плоскости. Это задание нагляднее характеризует положение плоскости и удобно для построения ее горизонталей.
3.1.1. Прямая в плоскости
Прямая принадлежит плоскости, если две точки прямой и плоскости имеют соответственной одинаковые отметки.
В плоскости можно провести прямую с различным уклоном, но не превышающим уклон плоскости.
|
|
|
