Краткие теоретические сведения

Учебно-методическое пособие

к лабораторной работе

«Анализ систем с помощью сетей Петри»

 

Уфа 2006

 

 

В учебно-методическом пособии изложены основы теории сетей Петри, принципы построения моделей систем в виде сетей Петри, методы определения их свойств и анализа динамических свойств моделируемых систем.

Пособие содержит задания к лабораторной работе и порядок ее выполнения.

 

Составитель Кирюшин О.В., доц., канд. техн. наук

 

 

Рецензент Новоженин А.Ю., ст. преподаватель

 

ã Уфимский государственный нефтяной технический университет, 2006

Цель работы

Изучение сетей Петри как методологии описания динамических свойств систем.

 

Краткие теоретические сведения

Сети Петри (СП) являются примером семантических сетей, представленных разновидностью ориентированных двудольных графов и предназначенных для моделирования динамических свойств различных систем (систем отношений между людьми, последовательностей действий при выполнении какой-либо работы и т.д.).

Двудольный граф включает вершины двух типов: позиции (обозначаются кружками) и переходы (обозначаются планками). Сеть Петри может быть формально представлена как совокупность множеств:

N = (P, T, G, W),

где P = {p₁, p₂… p_n} – множество всех позиций (n – количество позиций);

Т = {t₁, t₂… t_m} – множество переходов (m – количество переходов);

G = (G_p-t, G_t-p) – множество дуг сети:

G_p-t = (p´t), G_t-p = (t´p) – множества дуг, ведущих соответственно от переходов к позициям и от позиций к переходам (дуг, соединяющих однородные вершины, не существует);

W = {w₁, w₂… w_k} – множество весов дуг (k – количество дуг).

Каждая позиция может быть маркирована, т.е. содержать некоторое число маркеров. Если обозначить числа фишек, находящихся в i-й позиции p_i, как m_i, то маркировка всей сети: M = {m₁, m₂… m_n}. Тогда полное определение сети Петри, включая данные о начальной маркировке, можно записать в виде

PN = (N, M₀),

где М₀ – начальная маркировка сети.

При моделировании процессов принятия решений с помощью СП ее позиции интерпретируют собой некоторые условия, состояния, значения переменных и т.д. Переходы интерпретируют собой логические предложения (принятие решений), соответствующие выполнению действий, при этом входные позиции – условия выполнения действий, выходные позиции – результат выполнения действий. Действие (переход) связано с принятием какого-либо решения, которое инициировано определенными условиями и результатом которого является новое состояние (условие).

Другими словами, позиция – это имя существительное, а переход – глагол.

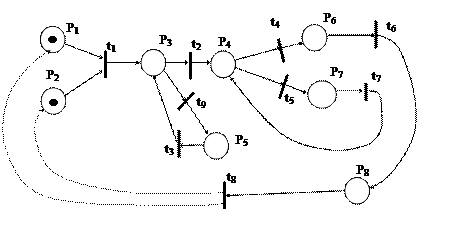Пример. Схема принятия решений при попытке получить деньги из банкомата (см. рисунок 1).

 

 

Рисунок 1 – Пример сети Петри

 

Смысл позиций: Р₁ – карта (ее наличие); Р₂ –банкомат исправен и свободен; Р₃ – введенный код; Р₄ – код набран правильно, запрашивается сумма; Р₅ – код набран неправильно; Р₆ – сумма доступна; Р₇ – сумма недоступна (нет такого количества денег на карте); Р₈ – деньги (получены). Смысл переходов: t₁ – банкомат принимает карту и делает запрос в банк, ввод кода; t₂ – запрос суммы; t₃ – повторный ввод кода; t₅ – выдача сообщения о недоступности суммы; t₆ – выдача денег; t₇ – повторный набор суммы; t₈ – забрать карту из банкомата (другой исход: имеется другая карта, с которой также нужно снять деньги – см. дуги, обозначенные пунктиром); t₉ – выдача сообщения, что код неверный.

То есть банкомат сможет принять карту только в том случае (переход t₁), если на руках имеется карта (позиция Р₁ символизирует ее наличие) И банкомат исправен (позиция Р₂). Если эти два условия выполняются, то банкомат принимает карту и просит ввести код (результат действия – введенный код, символизируемый позицией Р₃). Далее возможны два варианта развития событий: код оказывается правильным (в этом случае выполняется действие t₂ - запрос суммы) ИЛИ неправильным (в этом случае выполняется действие t₉ - выдается сообщение об ошибке). И так далее.¨

Роль указателей мощности потоков выполняют маркеры (●), также именуемые фишками и метками. Формально маркер – это знак выполнения соответствующего условия. В приведенном примере позиции Р₁ и Р₂ содержат по одному маркеру, что говорит о наличии одной карточки на руках и одного исправного банкомата. В позиции Р₃ маркера пока нет, т.е. банкомат пока не запрашивает код.

При выполнении условий переходы срабатывают, что приводит к перемещению маркеров по сети.

Правило срабатывания перехода: Переход срабатывает только в том случае, если во всех входных позициях имеется достаточное количество маркеров (по меньшей мере, по одному). При срабатывании перехода из входных позиций изымаются маркеры (в случае взвешенной СП изымается количество маркеров, соответствующее весам дуг, связывающих входные позиции с данным переходом), а в выходные – добавляются (для взвешенной СП – также соответственно весам дуг). Начальная маркировка СП есть начальное состояние системы. При срабатывании каждого перехода маркировка сети меняется.

Так, при срабатывании перехода t₁ в рассматриваемом примере (банкомат принимает карту и делает запрос кода) изымаются маркеры из позиций Р₁ и Р₂ и помещается один маркер в позицию Р₃. Это символизирует отсутствие карты на руках (она в банкомате) и свободного банкомата (вторую карту в него ввести нельзя), но при этом уже запрошен код.

В случае взвешенной СП количество перемещаемых маркеров соответствует весам дуг. Если во входной позиции маркеров больше, чем вес дуги, то забирается только часть маркеров. Например, при срабатывании перехода t₁₁ (рисунок 2,а) маркировка изменяется соответственно (рисунок 2,б). Видно, что общее число маркеров в сети изменилось.

В сети на рисунке 3 переход не сработает из-за недостатка маркеров в одной из входных позиций.

 

а) б)

Рисунок 2 – Срабатывание перехода

 

Рисунок 3

 

Таким образом, если осуществить начальную маркировку СП, то использованием формальных правил можно описать логику работы системы и произвести анализ ее работоспособности. Переходы маркеров описываются графом достижимости (ГД), у которого каждой вершине соответствует определенная маркировка, а каждой дуге – переход, который срабатывает при данной маркировке.

Таким образом, граф достижимости представляется как

GD = (V, E),

где V – массив вершин (маркировок, соответствующих вершинам):

V = {М₁, М₂ … М_q},

М_i – i-я маркировка, q – количество маркировок;

Е = {e₁, e₂ … e_p} – массив дуг, связывающих вершины (р – количество дуг).

Каждая дуга представляется как совокупность e_i = {a₁, a₂, Т}, где a₁ и a₂ – номера начальной и конечной вершин графа; Т = {t₁, t₂, … t_k} – массив переходов, соответствующий дуге; k – количество одновременно срабатывающих переходов при переходе от одной маркировки к другой.

Алгоритм построения графа по исходной СП:

1 За исходную берется маркировка М₀ и ей присваивается метка «новая».

2 Для каждой «новой» маркировки выполнять следующие операции:

2.1 Для «новой» маркировки М_нов определяются все переходы, которые могут быть запущены, а также все возможные комбинации этих переходов.

2.2 Для каждого разрешенного перехода или комбинации переходов производятся следующие действия:

2.2.1 Определяется маркировка М’, которая образуется при срабатывании данного перехода (комбинации переходов).

2.2.2 Просматриваются все маркировки на пути от М’ к начальной М₀. Если на пути находится маркировка М”, элементы которой больше либо равны соответствующим элементам новой и которая не равна М’, то вместо элементов m’_i, которые больше, чем элементы m_i маркировки М₀, записывается символ «w» (бесконечность). В массив Е записывается дуга с соответствующими a₁, a₂ и Т.

2.2.3 Просматриваются все маркировки графа. Если находится маркировка, равная новой, то в массив Е записывается новая дуга, у которой a₁ = a₂ и равны номеру найденной маркировки.

2.2.4 Если в п.п. 2.2 и 2.3 маркировки не найдены, то создается новая вершина графа, в которую записывается новая маркировка, в массив Е записывается дуга, у которой a₁ равна номеру исходной маркировки, a₂ - номеру новой маркировки, Т – набор переходов, срабатывание которых привело к переходу от одной маркировки к другой. Далее определяется массив всех разрешенных переходов и расчет продолжается, начиная с п. 2.2.

Для рассмотренного выше примера СП граф ГД имеет вид (рисунок 4), список маркировок приведен в таблице 1.

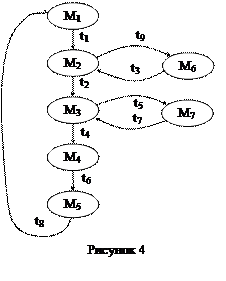Таблица 1

	(Р1 Р2 Р3 Р4 Р5 Р6 Р7 Р8)
М1	(11000000)
М2	(00100000)
М3	(00010000)
М4	(00000100)
М5	(00000001)
М6	(00001000)
М7	(00000010)

 

 

С помощью ГД могут быть определены свойства СП и, в конечном счете, моделируемой системы. К ним относятся:

- живость (отсутствие тупиковых состояний);

- ограниченность (сеть ограниченна, если символ «w» не входит ни в одну вершину графа);

- безопасность (сеть безопасна, если в метки вершин входят только «0» и «1») – физически безопасность означает отсутствие зацикливаний;

- правильность (если сеть безопасная и живая, то она правильная);

- обратимость (сеть обратима, если в графе имеется хотя бы одна дуга, направленная к начальной маркировке М₀);

- пассивность переходов (переход t_i пассивен, если он не соответствует ни одной дуге графа);

- число возможных состояний N_сост.

Сеть Петри называется k-ограниченной, если в любом состоянии в любой позиции скапливается не более k фишек.

Любая система должна представляться правильной сетью.

Для рассмотренного примера можно сделать вывод, что сеть правильная, обратимая и без пассивных переходов.

Определенные свойства СП характеризуют моделируемую систему. Так, если система моделируется живой сетью, то в системе отсутствуют состояния, после которых дальнейшие действия невозможны. В первом примере СП живая, значит банкомат не «зависнет» ни на каком этапе.

Практическое значение и наиболее ясную интерпретацию имеют два вида СП:

1) маркированные графы – каждая позиция такой СП должна иметь не более одного входного и одного выходного перехода;

2) автоматные сети (А-сети) – каждый переход такой СП должен иметь не более одной входной и одной выходной позиции.

3) сеть со свободным выбором (ССВ) – это ординарная сеть Петри, в которой каждая дуга из любой позиции представляет собой или единственную выходящую дугу, или единственную входящую дугу для какого-либо перехода.

СП моделируют очень широкий класс логических задач. Существует много разновидностей сетей. Главное их достоинство – возможность анализировать логический процесс по неизбыточным моделям. Кроме того, формализованные методы анализа СП в сочетании с возможностью декомпозиции дают возможность решать очень сложные задачи принятия решений.

Экспериментальная часть

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: