 |
Показатели корректности тестирования структуры программных модулей
|
|
|
|
Считаем, что программа представлена в виде графа.
Сложность теста равна числу дуг, входящих в i -ый маршрут, при исполнении этого теста.
Пусть 
- число условий в i -ом маршруте,
Каждое условие определяет выбор j-ой дуги к вершине 
.
Тогда 
= 
, где
Тогда 
- полная сложность тестов.
- число маршрутов по 
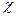критерию.
Пусть 
- вероятность обнаружения ошибки в j-ой дуге на i-ом маршруте.
Тогда вероятность получения правильного результата на i-ом маршруте
Реализация выбора j-ой дуги в i-ом маршруте зависит от конкретных входных данных. Пусть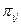 
- вероятность такой реализации.
Тогда 
- вероятность реализации i-ого маршрута.
Тогда 
-вероятность отсутствия проявления ошибки на i-ом маршруте.
Предположим, что правильность исполнения программы не зависит от предыдущих исполнений ее и равна 
.
Тогда 
- полная вероятность правильного функционирования программы, она же показатель корректности программы.
(1) – вероятность появления ошибки.
- может существенно меняться в зависимости от выбранного критерия .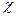
Оценка вероятности правильной работы программы при выделении маршрутов по 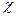критерию есть
.
Представляет интерес оценка изменения 
в зависимости от затрат на тестирование, которые характеризуются суммарным объемом тестов 
для 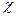критерия выделения маршрутов, число которых :
.
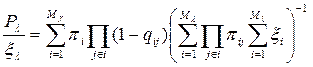При увеличении жесткости критериев выделения маршрутов увеличивается их число и замедляется рост корректности программ при возрастании сложности тестирования.
Если величина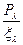 
мала, то корректность программ увеличивается медленно, и эффективность дальнейшего тестирования этим методом может оказаться сомнительной.
Полное тестирование при некотором 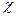-ом критерии выделения маршрутов может соответствовать некоторой вероятности обнаружения ошибки 
при выделении маршрутов по более жесткому
|
|
|
критерию. Разность - 
может использоваться для оценки целесообразности продолжения тестирования с переходом на более жесткий критерий выделения маршрутов.
Вероятность правильного функционирования программы зависит от значений , которые определяются прежде всего тем, насколько тщательно протестированы ветви программы к текущему моменту отладки. Об этих значениях можно сделать следующие предположения:
Гипотеза 
: При исполнении программы по нетестировавшемуся маршруту возможно получение на дуге ошибки, несмотря на то, что эта дуга уже проверялась в составе других маршрутов.
Т.е. = 0, после полного тестирования всех маршрутов через j -ую дугу, = 
в противном случае.
Эта гипотеза позволяет получить пессимистические оценки вероятности правильности исполнения программы после проведения тестирования части маршрутов.
Гипотеза 
: При завершении тестирования программы по некоторому маршруту вероятность сохранения ошибок в дугах этого маршрута убывает пропорционально относительному числу протестированных маршрутов.
Т.е. = до начала тестирования, 0 – после тестирования всех маршрутов, 
в противном случае, где 
- относительное число протестированных маршрутов, проходящих через j -ю дугу.
Эту гипотезу трудно использовать при анализе из-за необходимости учета для каждой дуги программы соотношения числа маршрутов, протестированных и еще не проверенных.
Гипотеза 
: Любая дуга программы, проверенная хотя бы в одном маршруте тестирования, проверена полностью и не содержит ошибок, которые могли бы появиться при других маршрутах исполнения программы.
Т.е. = 0, если дуга проверялась хотя бы один раз, - в противном случае.
Эта гипотеза соответствует оптимистическим оценкам вероятности правильного исполнения программы.
|
|
|
Вероятность 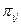выбора j -ой дуги при ветвлении в вершине графа программы в общем случае зависит от начальной части i-ого маршрута исполнения программы, по которому достигнута эта дуга. Для получения обобщенных результатов целесообразно предположить, что вероятность ветвления не зависит от предшествующей части маршрута исполнения программы.
Если вероятности ветвления в графе программы не известны, то можно предположить, что ветвления происходят равновероятно: 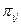=0,5.
Подставляя значения 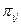и в формулу (1) можно оценить вероятность возникновения ошибки при первой или третьей гипотезах.
В книге [12, c.143] приведены результаты исследования зависимости Q от 
для 3 типов графов управления абстрактных ациклических программных модулей.
Полученные зависимости можно использовать для оценки эффективности тестирования реальных программных модулей.
|
|
|
