Статистический алгоритм разделения субъектов на классы профессиональной пригодности

Постановка задачи

Пусть информация о психологических особенностях человека содержится в я-мерном векторе ν (ν₁, ν₂,..., ν_n). Каждое из ν_i (i= 1, 2,..., n) – число, полученное при помощи той или другой методики (среди них могут быть определенным образом закодированы и качественные характеристики чело века). В дальнейшем компоненты ν будут называться признаками. Выбор признаков обычно производится с учетом психологических требований к профессиональной пригодности. Предлагаемый алгоритм позволяет отбросить те из используемых признаков, которые оказываются неинформативными для данной конкретной задачи определения профессиональной пригодности.

Предполагается, что группам лиц, с одной стороны, пригодных (группа «А»), а с другой стороны, непригодных (группа «В») к рассматриваемой деятельности соответствуют два класса я-мерных векторов {ν_Α} и {v_B}, которые могут сильно пересекаться, но статистически различны. В дальнейшем всегда будем считать, что {v_A} – класс векторов, характеризующих пригодных к данной деятельности субъектов.

С математической точки зрения задача определения профессиональной пригодности заключается в отнесении с определенной вероятностью ошибки вектора (ν₁, ν₂,..., ν_η) κ одному из двух классов – «А» или «В».

Имеется много различных методов решения этой задачи. Во всех методах необходим этап «обучения»: статистический анализ уже имеющегося опыта. Для целей определения профессиональной пригодности они не получили большого распространения – одни из-за крайней громоздкости и сложности применения даже при помощи вычислительных машин, другие потому, что оказались не очень эффективными.

Успех классификации по многим признакам в задачах диагностики зависит от информативности этих признаков и способа интеграции информации. Этот способ интеграции должен быть:

1) простым в вычислительном отношении и доступным при использовании;

2) малочувствительным к отсутствию какого-либо признака;

3) в какой-то мере инвариантным к сдвигу распределений признаков (последнее существенно в силу необходимости считаться с разными методическими условиями получения одного и того же признака).

Этим требованиям в значительной степени удовлетворяет алгоритм, основанный на модификации последовательного статистического анализа отношения вероятностей [58]. Он был предложен для диагностических целей и оказался весьма эффективным при дифференциальной диагностике ряда заболеваний по таким признакам, на основании которых постановка диагноза оказывалась затрудненной даже для опытных специалистов [63].

Для целей определения профессиональной пригодности этот алгоритм должен быть еще более эффективным, так как психологические признаки ν₁, ν₂,..., ν_η являются слабо статистически зависимыми, а при этих условиях последовательный анализ отношения вероятностей является оптимальной процедурой для классификации на два класса [64].

Алгоритм

Алгоритм состоит из двух этапов: первого – этапа обучения, во время которого накапливается информация о признаках на основании уже имеющегося опыта и оценивается информативность выбранных признаков, и второго – этапа классификации, на котором выносится решение о пригодности субъекта к определенной деятельности.

Обучение. Предполагается, что на основании предыдущего опыта можно выделить группы субъектов «А» и «В», которые отражают наше понимание пригодности (или непригодности) к данной деятельности и являются определенными эталонами для дальнейшего прогнозирования пригодности. Ряд практических вопросов, связанных с образованием классов «А» и «5», будет рассмотрен ниже. Далее предполагается, что имеется какой-то набор признаков ν₁, ν₂,..., ν_n, существенность которых для определения профессиональной пригодности можно и не знать. Теперь можно построить множество векторов {ν_Α} и {v_B}, соответственно характеризующих группы субъектов «А» и «В».

Процесс обучения состоит в получении оценки дискрет ных одномерных распределений вероятностей признаков ν₁, ν₂,..., ν_n для класса «А»: для класса «В»:

Предполагается, что ν₁, ν₂,..., ν_n слабо зависимы. Если, однако, этого нет, то для увеличения эффективности процедуры в рассмотрение вводятся сложные признаки – синдромы, определение которых можно получить на основании опыта и теоретических соображений или же используя соответствующий математический аппарат. Построение одномерных распределений существенно облегчает процесс обучения, а в случае слабой зависимости потери информации при этом невелики.

Если классы «А» и «В» многочисленны, то можно получить достаточно хорошую оценку требуемых вероятностей

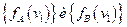(i=1,2,…,n)

В тех же случаях, когда численности классов «А» и «В» невелики, приходится прибегать к грубому квантованию признаков на 2–3–4 градации. Практическая проверка показывает, что при наличии в группе 25–30 человек и соответствующем квантовании можно получить удовлетворительные результаты.

Полученные в результате обследования данного контингента лиц показатели могут иметь различную ценность для целей прогнозирования профессиональной пригодности. Поэтому следующим этапом «обучения» является оценка информативности признаков.

Признак будет тем более информативным, чем больше различие между его распределениями у представителей класса «А» и «В». Оценка информативности признака ν, может выражаться величиной Ρ_j – вероятностью того, что распределения различны. Это достигается при помощи вычисления χ ². Интуитивно ясно, что вероятность Ρ может быть хорошей мерой информативности признака ν при данной конкретной классификации. Необходимо отметить, что признаки, информативные в одном случае, могут оказаться совсем не информативными для решения задачи профотбора других специалистов.

 

Вычисление с² производилось по формуле:

где 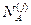и – общее число лиц соответственно в классах «А» и «В», данные которых использовались при построении распределений для j -го признака; и – частоты появления индивидов в i -йрадации j-го признака для сравниваемых классов; S – число градаций для j-го признака.

Вероятности Ρ_jпределялись по таблицам Л. Большова и Н. Смирнова [52]. Оценка информативности может быть также получена и при помощи расстояния Кульбака. В принятых здесь обозначениях и несколько измененной форме это расстояние имеет вид:

где

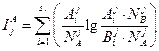и

Эта мера имеет ряд преимуществ, особенно при теоретических исследований. Для практики представляет интерес возможность измерения значимости признаков ν₁(j= 1, 2,...,n) отдельно для вынесения решения о принадлежности ν к {ν_Α} или {v_B} (соответственно слагаемые и ).

Используя ту или другую меру, признаки целесообразно расположить по их убывающей информативности, а те из них, которые неинформативны (Р слишком велико или I - мало), использовать не надо. Если окажется, что информативных признаков осталось мало, то необходимо ввести новые признаки.

Процесс «обучения» можно считать законченным, когда оценки распределений и (j= 1, 2,..., n ) достаточно надежны, признаки упорядочены по их информативности и их достаточно много.

Классификация (решающее правило). При классификации можно допустить две ошибки. Субъект из класса «А» может быть ошибочно отнесен к классу «B» и, наоборот, субъект из класса «B» может быть ошибочно причислен к классу «А». Первую из указанных ошибок классификации будем обозначать через α, а вторую через β.

Вероятности ошибок а и β определяются до проведения классификации. При выборе этих вероятностей должна быть учтена важность той или другой ошибки классификации, а также реальная ситуация, возникшая при решении данной конкретной задачи.

 

Пусть при обследовании субъекта S были получены признаки (они приведены здесь в порядке их убывающей информативности). Пусть на основании здравого смысла выбраны допустимые вероятности ошибок α и β. Рассмотрим отношение вероятностей, соответствующих первому признаку:

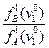
Если это отношение бeдет меньше чем:

то это будет означать, что полученное значение признака настолько вероятнее для класса «А», что можно с выбранным уровнем надежности (α, β) утверждать, что данное лицо относится к классу «А» (пригодно к данной профессиональной деятельности). Если это отношение

то с тем же уровнем надежности принимается решение о непригодности к рассматриваемой деятельности.

то информация, заключенная в признаке, недостаточна для отнесения к классам «А» и «B» и рассматривается следующий признак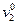

Если

то выносится решение об отнесении индивида в класс «А» если

то в класс «В». Когда же

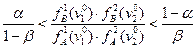
то рассматривается значение третьего признака и т. д.

Если, перебрав все признаки, не удается отнести субъекта к тому или иному классу с данным уровнем надежности, то есть рассматриваемое отношение не выходит за пределы требуемых рубежей, то это означает, что имеющиеся результаты обследования не позволяют сделать прогноз с выбранным уровнем надежности. В этих случаях можно понизить этот уровень и таким образом сделать прогноз или обратиться за дополнительной информацией.

При отсутствии дополнительной информации для минимизации вероятности ошибки целесообразно построить два распределения отношения правдоподобия по всем признакам соответственно для групп «А» и «В» и на основе этих распределений выбрать один порог. Особенности распределения обычно таковы, что этим порогом редко бывает 1.

Как известно, в схемах последовательного статистического анализа [58] процедуры обосновываются для однородного случая, когда

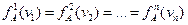и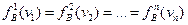

Однако нетрудно показать, что зависимость порогов от вероятности ошибок α и β переносится и на случай неоди наковых распределений, возникающих в диагностической задаче.

Практически удобно иметь дело не с отношениями вероятностей, а с логарифмом этого отношения. Тогда все вычисления сводятся к последовательному сложению.

Итак, определение принадлежности векторов ν (ν₁, ν₂,..., ν_n) к множеству {ν_Α} или {ν_Β} осуществляется следующим образом. Последовательно вычисляются величины L₁ L₂,..., L_k, где:

 

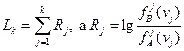
Каждое вычисленное L_k сравнивается с порогами

Если пр некотором k<n

То вычисляется L_k+1. Если же

То ; если же

Градация признаков

При использовании любых количественных методов для отбора приходится прибегать к квантованию признака, так как часто не удается достаточно точно измерить то или другое свойство человека, определяющее его индивидуальные психологические особенности. В таких случаях количество градации зависит от нашего умения дифференцировать данный признак Если признак измеряется достаточно точно (например, время реакции), то число градации можно объективизировать В данном случае, когда необходимо строить одномерные распределения признаков, число градаций в первую очередь зависит от количества лиц в обучающих группах Если число лиц достаточно велико, число градаций принимается равным 9–12

Если же число лиц невелико (25–30 человек), то квантование признака на диапазоны обеспечивается, исходя из особенностей получающихся гистограмм. На основании опыта установлено, что в таких случаях достаточно 2, 3, 4 диапазона. В ряде случаев, когда распределения имеют сложную форму, диапазоны градаций будут неодинаковыми.

Общим правилом здесь может быть указание, предписывающее делать такие диапазоны, при которых расстояние (например, X²) между соответствующими распределениями f_A (V) и f _в(V) будет наибольшим.

Выбор порога

В последовательной статистической процедуре отношения вероятностей предусматриваются два порога

где α, β – ошибки классификации, которые назначаются заранее Простая зависимость порогов от вероятностей ошибок классификации позволяет выбирать нужный порог, основываясь на сложившейся конъюнктуре

Необходимость выбора небольшого числа лиц из больших контингентов делает возможным определить а = b порядка 0,001 или даже 0,0001 С другой стороны, при ограниченном количестве лиц естественно выбрать α = β = 0,05 или даже 0,10

Если окажется, что ошибка пропустить хорошего специалиста и, наоборот, ошибка приема малопригодного неравноценны, то имеется возможность учесть это, выбирая разные вероятности α и β

Таким образом, выбор порогов является весьма гибким и учитывает реальную обстановку, а также цену возможных ошибок

Пример

Проиллюстрируем на примере изложенный выше алгоритм определения профессиональной пригодности по психологическим показателям

Разбиение на классы

В качестве исходного материала для составления дифференциально-диагностической таблицы были использованы результаты психологического обследования двух групп операторов, которых по объективным производственным показателям и характеристикам ведущих специалистов можно отнести к классу «хороших» («А») и «плохих» («В») специалистов.

Представители этих двух классов различались между собой по своей квалификации, а также, частично, по опыту работы.

Операторы, отнесенные к классу «А» (34 человека в возрасте 27–32 лет), прошли длительную подготовку по специальности и имели практический опыт работы в сложных системах управления. Все они характеризовались как специалисты высокой квалификации

Лица, объединенные в класс «В» (33 человека в возрасте 23–29 лет), имели более низкий уровень подготовки и выполняли операторскую деятельность в менее сложных системах управления.

Психологические показатели

Для оценки состояния ряда психологических качеств и психофизиологических функций был использован комплекс табличных тестов и аппаратурных методик, выбор которых определен требованиями к состоянию ведущих систем организма у данных специалистов.

Это:

1. Корректурная проба с кольцами: а) время выполнения задания в сек; б) относительная частота ошибок;

2. «Компасы» коэффициент успешности;

3. «Отыскивание чисел с переключением»: а) время выполнения задания в сек.; б) производительность – время выполнения одной операции в сек.; в) количество ошибок;

4.. 4. «Сложение с переключением»: а) производительность – количество сложений за мин.; б) величина различия в темпе работы; в) относительная частота ошибок;

5. «Перепутанные линии»: а) производительность – количество просмотренных линий за 10 мин.; б) количество ошибок;

6. «Расстановка чисел»: а) производительность; б) относительная частота ошибок;

7. «Память на числа» – воспроизведение сразу после экспозиции: а) коэффициент успешности:

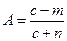
где с – общее число зафиксированных чисел, m – число ошибочно воспроизведенных чисел, n – число невоспроизведенных чисел; б) количество правильно воспроизведенных чисел;

8. «Память на числа» – воспроизведение через 30 мин. после экспозиции: а) коэффициент успешности; б) количество правильно воспроизведенных чисел;

9. «Реакция на движущийся объект»: а) относительная частота точных ответов:

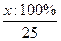
где х– количество точных ответов; б) суммарная величина отклонений от «0»;

10. Тремометрия – проведение стержня в прорези: а) количество касаний за 1 сек.; б) средняя продолжительность одного касания;

11. Тремометрия – удержание стержня в отверстии: а) количество касаний за 1 сек.; б) средняя продолжительность одного касания;

12. Рефлекс на время – 1 сек.: величина ошибки;

13. Рефлекс на время – 15 сек.: величина ошибки.

Построение распределений. Небольшое число лиц в группах «А» и «В» потребовало проведения грубого квантования, которое был сделано в соответствии с изложенными выше рекомендациями (см. 10.5.3). Диапазоны квантования приведены далее в таблице 15.

Полученные распределения, как правило, существенно отличаются от нормальных, а в ряде случаев имеют U –образную форму (например, показатель относительной частоты ошибок в корректурной пробе). Важно отметить, что для классов «А» и «В», вообще говоря, получены разные по форме распределения одного и того же признака.

Информативность признаков. Оценка признаков проводилась при помощи критерия χ².

Если Ρ > 0,10, то признак считался неинформативным.

В результате анализа было установлено, что некоторые признаки малоинформативны для различения классов и могут не рассматриваться. Необходимо отметить, что при других диапазонах квантования информативность признаков может быть несколько другой. Экспериментальное варьирование диапазонов в разумных пределах показало, что получающееся изменение информативности не очень существенно.

Построение диагностической таблицы. Теперь все готово для построения рабочей диагностической таблицы Для каждого информативного признака вычисляется логарифм отношения вероятностей для значений психофизиологических признаков, попадающих в соответствующие диапазоны, то есть для j-признака и i-диапазона (градации) вычисляются по формуле

Таблица 14

⇐ Предыдущая31323334353637383940Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: