Линейная парная регрессия

Регрессия [regression] – зависимость среднего значения какой-либо случайной величины от некоторой другой величины (парная регрессия) или нескольких величин (множественная регрессия).

Парная регрессия

Построение модели парной регрессия (или однофакторная модель) заключается в нахождении уравнения связи двух показателей у и х, т.е. определяется как повиляет изменение одного показателя на другой.

Уравнение модели парной регрессии можно записать в общем виде:

 

Уравнение линейной парной регрессии имеет вид: .

 

Для оценки параметров a, b методом наименьших квадратов (МНК) необходимо решить систему нормальных уравнений:

(1.1)

Можно воспользоваться готовыми формулами решения системы:

, ,

(1.2)

где – среднее значение фактора X;

– среднее значение результативной переменной Y;

– среднее значение произведения переменных X и Y;

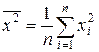– среднее значение квадрата переменной Х;

– ковариация переменных Х и Y;

– дисперсия переменной Х.

Коэффициент регрессии b показывает, на сколько единиц в среднем по совокупности изменится результирующая переменная Y, если факторная переменная Х увеличится на одну единицу.

 

Для оценки тесноты линейной связи между переменными используют линейный коэффициент парной корреляции:

,

(1.3)

где – среднеквадратическое отклонение (СКО) переменной Х;

– среднеквадратическое отклонение (СКО) переменной Y.

Можно считать, что:

1) если , то имеется прямая линейная связь между переменными Х и Y;

2) если , то имеется обратная линейная связь между переменными Х и Y;

3) если (), то линейная связь между переменными Х и Y отсутствует.

Качественная оценка тесноты связи величин Х и Y может быть выявлена на основе шкалы Чеддока:

Тестона связи	Значение коэффициента корреляции
Слабая	0,1-0,3
Умеренная	0,3-0,5
Заметная	0,5-0,7
Высокая	0,7-0,9
Весьма высокая	0,9-0,99

 

Для оценки качества уравнения регрессии использую коэффициент детерминации .

Коэффициент детерминации характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака (квадрат коэффициента корреляции):

.

(1.4)

Коэффициент детерминации показывает, какую часть вариации (изменения) результативной переменной Y объясняет вариация (изменение) фактора X. Чем ближе к единице, тем лучше регрессионная модель.

 

Оценка статистической значимости уравнения регрессии в целом осуществляется с помощью F-критерия Фишера. Проверяется гипотеза Н ₀ о статистической незначимости уравнения регрессии. Для этого рассчитывается фактическое значение критерия по формуле:

,

(1.5)

где n – число единиц совокупности;

m – число параметров при переменных х.

Если применяется линейное уравнение регрессии, то расчет F _факт упрощается:

.

(1.6)

F _табл – это максимально возможное значение критерия, которое могло сформироваться под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a – вероятность отвергнуть правильную гипотезу при условии, что она верна. Имеются таблицы критических (табличных) значений F-критерия: F (a; k ₁; k ₂), где , . Для линейного уравнения парной регрессии с уровнем значимости a = 0,05 необходимо в таблице значений (приложение №4) найти значение F (0,05; 1; n – 2).

Если F _табл < F _факт, то гипотеза Н ₀ о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность.

 

Для оценки статистической значимости коэффициентов регрессии и коэффициента корреляции рассчитывается t-критерий Стьюдента. Выдвигается гипотеза H ₀ о случайной природе показателей, т.е. о незначимом их отличии от нуля. Наблюдаемые значения t-критерия рассчитываются по формулам:

, , ,

(1.7)

где – случайные ошибки параметров линейной регрессии и коэффициента корреляции.

Для линейной парной регрессии выполняется равенство , поэтому проверки гипотез о значимости коэффициента регрессии при факторе и коэффициента корреляции равносильны проверке гипотезы о статистической значимости уравнения регрессии в целом.

Вообще, случайные ошибки рассчитываются по формулам:

, , .

(1.8)

где – остаточная дисперсия на одну степень свободы:

.

(1.9)

Табличное (критическое) значение t-статистики находят по таблицам распределения t-Стьюдента при уровне значимости α = 0,05 и числе степеней свободы . Если t _табл < t _факт, то H ₀ отклоняется, т.е. коэффициенты регрессии не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора.

 

Поделиться:

Воспользуйтесь поиском по сайту: