 |
Относительные показатели, их виды
|
|
|
|
Лекция 5. Обобщающие статистические показатели
1. Абсолютныепоказатели, их виды
Обобщающие статистические показатели – отражают количественную сторону изучаемой совокупности и служат базой анализа и прогнозирования социально-экономического развития отдельных предприятий, регионов и страны в целом. В зависимости от исследуемого признака обобщающие показатели выражаются через абсолютные, относительные и средние величины.
Абсолютные величины представляют собой характеристику всего исследуемого явления по отдельно взятому признаку. Абсолютные величины являются результатом первичного учета, заключающегося в первоначальной регистрации предметов, событий хозяйственной деятельности, отражаемой в соответствующей документации (накладных, актах, квитанциях и т.д.). Например:
а) признак протяженности и размерности (длина автомобильных дорог региона, выражаемая в километрах; размер жилой площади в регионе, выражаемая в квадратных метрах, и т.д.);
б) признак численности единиц совокупности (число сотрудников на предприятии; число машин в автопарке, и т.д.);
в) признак, характеризующий количественную сторону явления, состоящего из нескольких объектов или находящегося под влиянием нескольких признаков, (объем произведенной продукции в стоимостном выражении, который зависит от множества факторов, например: себестоимость единицы продукции, количество произведенной продукции, производительность труда рабочих, численность рабочих и т. д.); товарооборот (объем проданной продукции в стоимостном выражении), на который влияют цена единицы продукции и количество таких единиц; и др.)
По степени охвата исследуемой совокупности выделяют несколько видов абсолютных величин:
|
|
|
1) индивидуальные, характеризующие отдельные единицы совокупности (например, масса единицы произведенной продукции, выраженная в граммах). Их получают на первом этапе статистического исследования (на этапе статистического наблюдения) как результат замера, взвешивания, подсчета;
2) общие, отражающие размеры признака в совокупности в целом (например, численность населения Российской Федерации на начало определенного года). Их получают на втором этапе – на этапе сводки и группировки.
Поскольку абсолютные показатели – основа всех форм учета и приемов количественного анализа, то следует разграничивать моментные и интервальные абсолютные показатели.
Моментные – показывают фактическое наличие или уровень явления на определенный момент, т.е. на дату, например, наличие товарных запасов, объем незавершенного производства.
Интервальные – итоговый накопленный материал за какой-либо период, и в отличие от моментных, допускается их последующее суммирование.
Абсолютные величины всегда именованы, то есть всегда имеют определенные единицы измерения. Выделяют натуральные, условно-натуральные, стоимостные и трудовые единицы измерения.
Натуральные единицы измерения используются в случае изучения свойств объекта исследования. Например, объем экспорта нефти оценивается в баррелях и тоннах, строительство дорог – в километрах, и т.д.
При необходимости совместного исследования различных типов одного и того же явления, выраженного в натуральных измерителях, применяется условно-натуральный измеритель. Он выражает наиболее характерный для явления размер признака, присущий определенному типу этого явления.
Примеры условно-натуральных единиц измерения, применяемых в российской статистике:
1) условное топливо, теплосодержание которого принимается равным 29,3076 МДж. Например, 100 т торфа будут эквивалентны 81,9 тоннам условного топлива, а 100 тонн нефти – 153,6 тоннам условного топлива;
|
|
|
2) условное мыло, содержащее 40% жирных кислот;
Стоимостные единицы измерения абсолютных величин позволяют изучать различные по своему содержанию явления, несопоставимые в натуральных единицах измерения. Кроме того, стоимостные измерители позволяют оценить исследуемое явления в денежном выражении, что также является важным при проведении экономического анализа.
Значимость стоимостных единиц измерения заключается в их применении при расчете макроэкономических показателей, отражающих общий уровень развития страны, например внутреннего валового продукта, национального дохода и др.
Трудовые единицы измерения применяются для учета затрат рабочего времени и расчета производительности труда (чел-час, чел-дн.)
Относительные показатели, их виды
Относительная величина – обобщающий показатель, который дает числовую меру соотношения 2-х абсолютных величин.
Основное условие правильного расчета относительных показателей – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями.
При расчете относительных величин – абсолютный показатель, находящийся в числителе, называется текущим или сравниваемым, абсолютный показатель, с которым производится сравнение, находящийся в знаменателе, называется основанием или базой сравнения.
Относительная величина показывает, во сколько раз сравниваемая величина больше или меньше базисной или какую долю первая составляет по отношению ко второй. В ряде случае относительная величина показывает, сколько единиц одной величины приходится на единицу другой.
В результате сопоставления одноименных абсолютных величин получают неименованные относительные величины. Они могут выражаться в виде долей, кратных соотношений (например, 1:2), процентов (если база сравнения взята за 100%), в виде промилле (если база сравнения взята за 1000%0), в виде продецимилле (если база сранения взята за 10000%00) и т.д.
Результатом сопоставления разноименных величин являются именованные относительные величины. Их название образуется сочетанием сравниваемой и базисной абсолютных величин (например, чел/км2 и т.д.)
|
|
|
По своему познавательному значению относительные показатели подразделяются на следующие виды: плана; выполнения плана, динамики, структуры, координации, сравнения и интенсивности.
Относительный показатель плана (ОПП) представляет собой отношение плановой величины (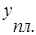
) к величине, достигнутой в прошлом периоде (
):
;
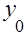Он показывает, во сколько раз намечаемый объем производства превышает достигнутый уровень, или сколько процентов от этого уровня составит.
Относительный показатель выполнения плана (ОПВП) – показатель, характеризующий уровень выполнения предприятием своих обязательств, предусмотренных в договорах;
Расчет производится путем соотношения фактически достигнутого объема в текущем периоде (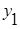
)и объема обязательств по договору (
. Выражается в процентах или коэффициентах:
Относительный показатель динамики (ОПД) – характеризует изменение изучаемого явления во времени, выявляет направление развития, измеряет интенсивность развития. Рассчитывается отношением величины текущего периода (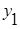) к величине одного из прошлых периодов ():
;
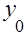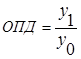Рассчитанный показатель показывает, во сколько раз текущий уровень превышает предшествующий или какую долю от последнего составляет.
Произведение относительного показателя плана на относительный показатель выполнения плана дает относительный показатель динамики:
Различают ОПД с постоянной и переменной базой сравнения. Если сравнение осуществляется с одной и той же базой сравнения, то получается ОПД с постоянной базой, при расчете с ОПД с переменной базой сравнения сравнение осуществляется с предшествующим уровнем.
ОПД с постоянной базой равен произведению ОПД с переменной базой, взятых в виде коэффициентов за весь анализируемый период.
Относительный показатель структуры (ОПС) – характеризует состав изучаемых совокупностей и исчисляется как отношение абсолютных величин каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. отношение части (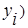
к целому (
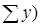(удельный вес части в целом). Выражается в процентах или долях:
|
|
|
;
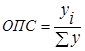Относительный показатель координации (ОПК) – характеризует соотношение между отдельными частями статистической совокупности:
;
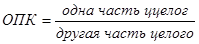Относительный показатель сравнения (ОПСр) – характеризует количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения, например, товарообороты различных предприятий:
;
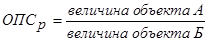Относительный показатель интенсивности (ОПИ) – характеризует степень распространения изучаемого явления в присущей ему среде, например количество магазинов на 1000 человек и рассчитывается соотношением двух разноименных величин, связанных между собой:
.
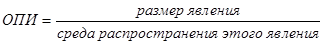3. Средние величины, их сущность и значение
Средняя величина – это обобщающая количественная характеристика признака в статистической совокупности в конкретных условиях места и времени.
Важнейшее свойство средней величины заключается в том, что она представляет значение определенного признака во всей совокупности одним числом, несмотря на количественные различия его у отдельных единиц совокупности, и выражает то общее, что присуще всем единицам изучаемой совокупности. Таким образом, через характеристику единицы совокупности она характеризует всю совокупность в целом.
Благодаря этому средняя величина получает большое значение для выявления закономерностей, присущих массовым явлениями, незаметных в единицах.
Признак, по которому находится средняя, называемый осередняемым признаком и обозначается буквой " х"
". Такой способ обозначения указывает на происхождение средней из конкретных величин. Черта сверху символизирует процесс осреднения индивидуальных значений. Численность каждой варианты обозначают через f.
Виды средних величин
Все используемые на практике средние величины можно подразделить на следующие виды: средняя арифметическая простая и взвешенная; средняя гармоническая простая и взвешенная; средняя геометрическая, средняя квадратическая, средняя кубическая.
Среднюю арифметическую взвешенную можно определить как частное от деления суммы произведений вариантов на их частоты (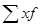
) и суммы частот (
):
. = 
,
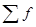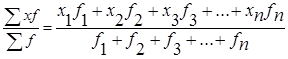Когда веса (частоты) отсутствуют или равны между собой (f1=f2=...= fn), применяется средняя арифметическая простая:
Средняя величина обладает рядом математических свойств, знание которых облегчает ее расчет.
|
|
|
Основные свойства средней арифметической
1. От уменьшения или увеличения частот каждого значения признака х в А раз величина средней арифметической не изменится.
2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:
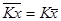
3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:
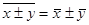
4. Если х = с, где с - постоянная величина, то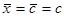 
.
5. Сумма отклонений значений признака Х от средней арифметической х равна нулю:
6. Если от каждого варианта вычесть или к каждому варианту прибавить какое-либо постоянное число А, то средняя уменьшается или увеличивается на то же самое число А
Средняя гармоническая – это величина, обратная средней арифметической.
Как и средняя арифметическая, она может быть простой и взвешенной. Применяется она тогда, когда необходимые веса (f) в исходных данных не заданы непосредственно, а входят сомножителем в одни из имеющихся показателей.
Средняя гармоническая простая рассчитывается по формуле:
,
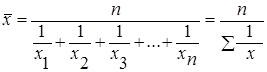т.е. это обратная величина средней арифметической простой из обратных значений признака.
Например, бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй - 15 мин., третий - 11, четвертый - 16 и пятый - 14 мин. Определите среднее время, необходимое на изготовление одной детали.
На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:
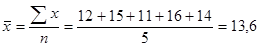
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей.
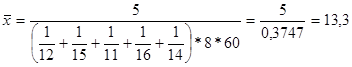мин.
Средняя гармоническая взвешенная:
= 
Например, необходимо определить среднюю урожайность всех технических культур на основании следующих данных (таблица 3):
Таблица
Валовой сбор и урожайность технических культур по одному из районов во всех категориях хозяйств.
| Культуры | Валовой сбор, ц ( )
| Урожайность, ц/га (x) |
| Хлопчатник Сахарная свекла Подсолнечник Льноволокно | 97,2 601,2 46,3 2,6 | 30,4 467,0 11,0 2,9 |
| Итого | 743,3 | Х |
Здесь в исходной информации веса (площадь под культурами) не заданы, но входят сомножителем в валовой сбор, равный урожайности, умноженной на площадь W = x*f, поэтому 
, а средняя урожайность будет равна 
.
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение кпредыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста.
Средняя геометрическаяисчисляется извлечением корня степени и из произведений отдельных значений — вариантов признака х:
где n — число вариантов; П — знак произведения.
Наиболее широкое применение средняя геометрическая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения.
Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
,
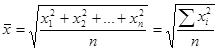где x1,x2,…xn- значения признака, n- их число.
Средняя квадратическая взвешенная:
,
где f-веса.
Средняя кубическая простая является кубическим корнем из частного от деления суммы кубов отдельных значений признака на их число:
,
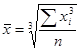где x1,x2,…xn- значения признака, n- их число.
Средняя кубическая взвешенная:
,
где f-веса.
Средние квадратическая и кубическая имеют ограниченное применение в практике статистики. Широко пользуется статистика средней квадратической, но не из самих вариантов x, и из их отклонений от средней (х —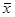 
) при расчете показателей вариации.
Средняя может быть вычислена не для всех, а для какой-либо части единиц совокупности. Примером такой средней может быть средняя прогрессивная как одна из частных средних, вычисляемая не для всех, а только для "лучших" (например, для показателей выше или ниже средних индивидуальных).
5. Структурные средние величины
Для характеристики структуры совокупности применяются особые показатели, которые называются структурными средними.
К таким показателям относятся мода и медиана.
Мода Mo - наиболее часто повторяющееся значение признака (чаще всего встречающийся вариант). Широко используется в коммерческой практике при изучении покупательского спроса, регистрации цен.
В дискретном ряду Мо - это вариант с наибольшей частотой, например:
| Размер обуви | ||||||||
| Количество реализованных пар |
В данном случае Мо=88.
В интервальном ряду Мо приближенно считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту (частость). В пределах модального интервала и нужно найти то значение признака, которое является модой. Конкретное значение для интервального ряда определяется формулой:
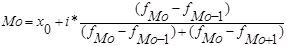
где, Хо – нижняя граница модального интервала,
i – величина модального интервала,
fMo-1, fMo,, fMo+1 – частоты соответствующие предмодальному, модальному и послеиодальному интервалам.
Например, имеются следующие данные о распределении работников по стажу работы:
| Стаж, лет | до 2 | 2-4 | 4-6 | 6-8 | 8-10 | св. 10 |
| Число работников |
35-20 15 15
Т.о. Мо = 6+2*--------------------=6+2*--------=6+2*---=6,7года.
(35-20)+(35-11) 15+24 39
Медиана (Ме) – величина, которая делит численность упорядоченного ряда на 2 равные части.
В дискретных вариационных рядах с нечетным числом единиц совокупности - это конкретное численное значение в середине ряда. Так в группе студентов из 27 человек медианным будет рост у 14-го, если они выстроятся по росту. Если число единиц совокупности четное, то медианой будет средняя арифметическая из значений признака у двух средних членов ряда. Так, если в группе 26 человек, то медианным будет средний рост 13-го и 14-го студентов.
В интервальном ряду порядок нахождения медианы следующий: ранжируем ряд, определяем накопленные частоты, по полученным данным находим медианный интервал. Т.к. Ме делит численность ряда пополам, значит, Ме располагается там, где накопленная частота составляет половину всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.
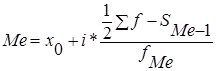
где х0 – нижняя граница медианного интервала,
i - величина медианного интервала,
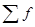- сумма частот ряда,
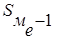– сумма накопленных частот, предшествующих медианному интервалу,
fMe – частота медианного интервала.
50-47
Ме=6+2*------------=6,17года
К медиане примыкают:
- квартили - делят совокупность на 4 равные части по 25%,
- квинтили – на 5 равных частей по 20%,
- децили – на 10 равных частей по 10%,
- персентили – на 100 равных частей.
|
|
|
