 |
Глава 2. Нетрадиционные формы организации обучения
|
|
|
|
Урок-практикум
Математический материал, изучаемый в V - VI классах, дает большой простор для составления задач, отражающих вопросы экономии и бережливости. Такие задачи не только способствуют закреплению навыков работы с натуральными и дробными числами, процентами, но и знакомят с экономической жизнью города, учат бережному отношению к народному достоянию, содействуют выработке активной жизненной позиции.
Для работы с учащимися составляются карточки-задания. При составлении заданий учитель использует различные материалы, публикуемые в региональной периодической печати, справочники по сельскому хозяйству, промышленному производству, экономические словари.
Учащимся предлагается на основании собранного материала составить задачу, записав ее условие, и решить ее. На следующем уроке 2-3 ученика зачитывают составленные задачи, а учитель вместе с классом комментирует их, выделяя моменты экономии и бережливости. Наиболее удачные задачи используются затем при повторении.
Например: За счет сокращения потерь сырья и материалов Полярный хлебозавод планирует в 2001 г. сэкономить муки на 200000 руб. Определите прибыль хлебозавода после реализации сверхплановой продукции, если 1 кг муки стоит 8 руб., на выпечку одного батона идет 400 г муки, а батон стоит 7 руб.
Другой способ составления задач - по готовым плакатам. Учащимся предлагается составить смету ремонта подъезда, класса, квартиры, используя данные плаката.
Например: Какое количество кафельной плитки необходимо для покрытия стен кабинета обслуживающего труда, если размеры плитки 15 см * 22 см? Выполните необходимые измерения самостоятельно. Во сколько обойдется покупка плитки, если каждая плитка стоит 10 руб.?
|
|
|
Вычислите, какое количество краски потребуется для окраски:
а) окон и дверей классного помещения;
б) всего школьного здания при предстоящем (во время летних каникул) ремонте школы?
Сделайте сами необходимые измерения.
Особый интерес вызывают у детей практические работы, выполняя которые самостоятельно или с помощью родителей, они могут составить семейный бюджет, подсчитать экономию электроэнергии.
Приведем примеры таких задач.
. Используя показания счетчика на 1 июня и 1 июля, I декабря и I января, определите, на сколько больше платили за электроэнергию в один из более темных месяцев года по сравнению с оплатой за один из более светлых месяцев, если стоимость 1 кВт * ч энергии равна 34 коп.
. В таблице указаны стоимость (в рублях) продукции, которую выпустил Полярный хлебозавод в I квартале текущего года. Постройте круговые диаграммы выпуска кондитерских хлебобулочных и шоколадных изделий.
. Используя данные таблицы, постройте диаграмму объема реализации промышленной продукции трудящимися нашего города.
. Постройте диаграмму роста расходов на социально-культурные мероприятия в нашем городе.
. На рисунке приведена диаграмма объема реализации промышленной продукции трудящимися нашего города. Перенесите числовые данные диаграммы на координатную плоскость, соедините построенные точки плавной линией и, используя полученный график, определите:
а) объем реализованной продукции в октябре и ноябре месяцах;
б) месяц, в котором объем реализованной продукции был наименьшим;
в) месяц, в котором объем реализованной продукции был наибольшим;
г) месяцы, когда был перевыполнен план по объему реализованной продукции.
Воспитание бережливости нельзя сводить только к решению соответствующих задач. Здесь важен весь комплекс проводимых мероприятий. Экскурсии на заводы, школьный «Рейд бережливых» должны дополнять друг друга и одновременно служить материалом для новых задач.
|
|
|
. После уроков в партах нашего класса были оставлены листы бумаги обшей массой в 1 кг. Если такое будет происходить каждый день, то сколько бумаги будет израсходовано напрасно:
а) в школе за 210 учебных дней в году;
б) во всех школах города за этот же период?
Какая часть всей бумаги, произведенной в нашей стране (около 6 тыс. тонн), будет потрачена впустую?
. После обеда в школьной столовой отходы хлеба составили 1 кг 100 г. Если бы такие отходы оставались каждый день, то сколько хлеба было бы неправильно использовано в школе за 210 учебных дней?
Какова стоимость этого хлеба, если 1 булка белого хлеба (весом 400 г) стоит 7 руб.? Сколько учеников из малообеспеченных семей смогла бы кормить школа на эти средства весь учебный гол, если на питание одного школьника требуется 308руб. в месяц?
. Измерьте площадь одной страницы учебника.
Определите, какова площадь всей бумаги, из которой изготовлен один экземпляр учебника.
Посмотрите, каков тираж учебника, и вычислите, сколько бумаги (м3) израсходовано на изготовление всех экземпляров учебника.
Для производства 1000 м2 бумаги требуется вырубить лес с  га. С какой площади потребовалось вырубить лес, чтобы выпустить весь тираж учебника?
га. С какой площади потребовалось вырубить лес, чтобы выпустить весь тираж учебника?
Решая такие задачи, ребята начинают лучше представлять, во что обходится государству и родителям их обучение, каков масштаб их школьных дел, к чему приводит расточительность и т.д.
Для решения задач по экономической тематике желательно подбирать задания, при решении которых необходимо произвести несложный экономический расчет. В ходе решения этих задач школьники могут уяснить смысл таких понятий, как себестоимость, расценка, прирост продукции, прибыль, рентабельность, сверхплановая продукция.
Например: Совхоз «Полярная звезда» продал государству 2,8 тыс. т молока по плану по цене 1500 руб. за тонну. Увеличив затраты на 500 тыс. руб., он получил дополнительно 0,4 тыс. т молока и уровень рентабельности производства повысился на 4%. Какую прибыль получил колхоз, если за сверхплановую продажу молока была установлена надбавка 30% к закупочным ценам?
При рассмотрении задач с экономическим содержанием в V - VI классах можно использовать и задачи на отыскание наилучшего решения, правда, пока только такие, в которых наилучшее решение можно определить путем сравнения полученных результатов.
|
|
|
Для кормления коров в совхозе «Тулома» требуется произвести 120 тыс. кормовых единиц ячменя или овса. Определите, что выгоднее производить, если известно, что 1 кг овса содержит 1 кормовую единицу, а 1 кг ячменя - 1,21 кормовой единицы и что производство 1 ц овса обходится хозяйству в 4 руб., а 1 ц ячменя в 4 руб. 30 коп.?
На примере решения несложных задач можно показать учащимся, как добиться экономии материальных средств, как обеспечить получение данного результата при минимуме затрат или получить максимальный результат, используя известный объем ресурсов.
. До реконструкции на ферме совхоза «Полярная звезда» работало 60 доярок, которые обслуживали 1200 коров. После реконструкции 28 операторов стали обслуживать 1680 коров. Во сколько раз увеличилось число коров, обслуживаемых одним человеком? На сколько возросла производительность труда оператора по сравнению с производительностью труда доярки?
. За счет сокращения потерь сырья и материалов, внедрения передовой технологии предприятия нашего города планируют сэкономить 17 тыс. кВт * ч электроэнергии. Какую часть составляет экономия Полярного хлебозавода, если он сэкономил 2 тыс. кВт ч? (Сколько процентов составляет экономия хлебозавода, если он сэкономил 2 тыс. кВт * ч?)
. В колхозе «Северная звезда» собрали с 1 га 60,8 и кормовых культур. После внедрения нового сорта морозостойких трав, урожай увеличивается на 25%. Сколько кормов собирает теперь колхоз с 23 га? На сколько гектаров можно уменьшить посевные площади, чтобы получать прежний объем кормов?
Решения подобных задач помогают учащимся понять, что эффективность общественного производства зависит не только от увеличения выработки продукции, но и от рационального, экономного использования времени, сырья, материалов, улучшения качества выпускаемой продукции, и убеждают их в том, что экономия - это результат предварительно продуманных действий.
|
|
|
Урок-мастерская
Урок-мастерская нацеливает учащихся на то, чтобы они собственным трудом добывали знания. В этом - основной лейтмотив развивающей педагогики. Тема «Степенная функция» очень подходит для творческой работы всего класса, так как степенная функция (у = хn, где n - любое рациональное число) - это фактически множество функций, имеющих различные свойства в зависимости от показателя степени.
Обсуждение этих свойств лучше всего организовать по группам. Для этого класс целесообразно поделить на шесть групп.
Прежде всего, учителю необходимо представлять себе последовательность работы в «мастерской»:
I этап - индукция - обращение к предыдущему опыту;
II этап - обсуждение темы в группах, а далее со всем классом;
III этап - разрыв - момент, когда учащиеся должны осознать, что в их знаниях имеются пробелы, которые они сами должны восполнить;
IV этап - рефлексия - определение степени усвоения.
Опишем подробнее каждый из этапов урока.
I этап - индукция. Учитель напоминает о том, что в классе уже изучат функции у=х, у=  , у=x2 их свойства и графики. Эти функции можно в общем виде задать формулой: у=хq, где q - некоторое целое число. Такая функция называется степенной. Перед классом ставится следующая задача: перечислить вопросы, на которые мы должны ответить, изучая новую функцию.
, у=x2 их свойства и графики. Эти функции можно в общем виде задать формулой: у=хq, где q - некоторое целое число. Такая функция называется степенной. Перед классом ставится следующая задача: перечислить вопросы, на которые мы должны ответить, изучая новую функцию.
Класс обсуждает эти вопросы по группам, а потом все вопросы от групп собираются в единый список:
Какими свойствами обладает данная функция?
Каков ее график?
В каких ситуациях она используется?
Начнем с ответа на последний вопрос. Приведем примеры нескольких ситуаций, в которых появляется степенная функция.
Три ученика поочередно выходят к доске и делают сообщения, подготовленные дома.
Первый ученик рассматривает функцию
S = 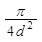
где S - площадь поперечного сечения провода диаметром d. Слушатели замечают, что эта степенная функция фактически представляет собой квадратичную, но с ограничениями на значение аргумента d.
Второй ученик рассказывает о том, что сила притяжения F двух тел с массами m1, и m2, выражается формулой F=γm1m2r-2. Это функция расстояния г между этими телами. В классе найдется ученик, который заметит, что мы уже строили график функции такого вида, хотя специально ее не изучали.
Третий ученик анализирует дальность d расстояния горизонта от наблюдателя: d=3,8h1/2. Эта функция высоты, на которую поднят наблюдатель над уровнем моря. Если ребята сами этого не заметили, то учитель должен подчеркнуть, что здесь величина d не может возрастать неограниченно. Действительно, как бы ни был высоко поднят наблюдатель, он не может увидеть больше, чем позволяют возможности его зрения и выпуклость Земного шара. Этот пример особенно показателен, так как позволяет судить о целесообразности ограничений на значения функции. Здесь какие-то ограничения мы должны наложить на значения функции d, хотя значения h, теоретически говоря, могут возрастать неограниченно.
|
|
|
II этап - обсуждение темы. Учащимся предоставляется некоторое время для того, чтобы они разобрали свойства одной из выбранных ими степенных функций. Главная проблема здесь в выборе функции. Одна группа склонна упрощать задачу, ограничиваясь функцией вида у = х2, которая всем учащимся хорошо известна. Другая группа слишком усложняет свою работу, занявшись функцией вида y=х4 или у=х5, а то и обеими вместе, хотя общий подход к вопросу учащимся еще не ясен.
В конце концов, находятся группы, избравшие функции, графики которых уже рассматривались ранее, хотя на них не делалось нужного акцента.
Первая группа рассматривала функцию вида у=х3; отметила область ее определения: D(f)=(-∞; +∞) и нулевое значение функции при х = 0. Ребята особо остановились на том, что функция возрастает на всей области определения. Выделили промежутки, на которых функция больше или меньше нуля. Выступавшие особо подчеркнули, что эта функция нечетная и не имеет ни наибольшего, ни наименьшего значения.
От этой группы выступает перед классом один ученик, который рассказывает о результатах исследований в группе.
Вторая группа выбрала для рассмотрения функцию у=х-3. Ребята заметили, что теперь придется исключить из области определения функции число 0, т.e. D(f)=(-∞; 0) U (0; +∞). В отличие от предыдущей, эта функция не имеет нулей. Но, как и рассмотренная выше, эта функция положительна при х > 0 и отрицательна при х < 0. Она убывает на всей области определения.
Представитель этой группы особо подчеркивает различия между функциями у = х3 и у = х-3.
Еще двое учеников рассказывают о функциях у = х4; у = х-4.
Во время своих выступлений все докладчики должны продемонстрировать графики рассмотренных функций.
Во время III этапа урока учащиеся должны обобщить свои знания. А сделать это они должны самостоятельно, удивившись разнообразию рассмотренных функций. «Почему им дано одно название, если их так много и они разные?» - вот вопрос, который должны поставить перед собою учащиеся. Задача учителя - незаметно подвести учащихся к этому вопросу. Наступает момент так называемого разрыва, когда ребята должны осознать недостатки своих знаний, их ограниченность или неполноту. Действительно, одна функция из рассмотренных имеет нули, другая нет. Одна возрастает на всей области определения, другая - то возрастает, то убывает. Какую же характеристику мы должны дать всей степенной функции, чтобы она охватывала как можно больше частных случаев?
В поиске ответа на этот вопрос кто-то из ребят, в конце концов догадывается, что вид степенной функции у = хn удобно связать с четностью или нечетностью показателя степени n.
Теперь уместно снова дать задание группам обсудить свойства функций:
у = хn
где n - нечетное;
у = хn
где n - четное,
у = х-n
где n - нечетное;
у = х-n
где n - четное.
Еще раз отмечаем план исследования функции:
. Указать область определения.
. Определить четность или нечетность функции
(или отметить, что она не является ни четной, ни нечетной).
. Найти нули функции, если таковые существуют.
. Отметить промежутки знакопостоянства.
. Найти промежутки возрастания и убывания.
. Указать наибольшее или наименьшее значение функции.
Работа завершается тем, что на доске возникают графики рассмотренных функций (рис. 1, а-г). Эти графики выполняют представители каждой из групп.

Рис. I
Теперь вместе с классом строим графики функции у = х1/n, у =x -1/n, где n - натуральное число и n ≥ 2 (рис. 2, а. 6).


Рис. 2
Отмечается общее свойство этих функций: они обе имеют область определения - промежуток (0; +∞). Они обе являются ни четной, ни нечетной. Они обе больше нуля.
Но у этих функций есть и различия. Ребята их называют особо: функция вида у = х1/n возрастает на своей области определения, а функция вида у = х-1/n убывает на той же области. Функция вида у = х1/n имеет нулевое значение при х = 0, а функция вида у = х-1/n не имеет нулей.
На IV этапе учащиеся должны заняться рефлексией, т.е. определением степени усвоения материала. Весь класс получает следующее задание по рис. 3.

Рис. 3
На рис. 3, а-з схематически изображены графики функций, которые заданы формулами: у = х3; у = x1/3; y=x4; у = х2; у = 1/x2; у=x1/2; y = х-1, у = х-1/2.
Установите, какая формула из данного списка примерно соответствует каждому из графиков а-з.
Учебные викторины
Одной из нетрадиционных форм обучения является учебная викторина. Она нацеливает учащихся на интерес к математике, развивает их умственные способности, заставляет их мыслить нетрадиционно. Рассмотрим несколько примеров проведения математических викторин в 11 и 5 классах.
Математическая викторина 5 класс.
Математическую викторину можно провести в виде "Рыбки»
1. Из плотной цветной бумаги изготавливается несколько рыбок

. На чистой обратной стороне пишется задача

. К каждой рыбке прикрепляется большая железная скрепка
. Все рыбки с задачами помещаются в ящик
. Представители команд вылавливают рыбки из ящика с помощью удочки (палочки с веревочкой, на конце которой прикрепляется магнит)
. Пойманные задачи решаются учениками и оцениваются баллами.
Задачи для "Рыбки"
. В комнате четыре угла. В каждом углу сидит кошка. Против каждой кошки сидят по 3 кошки. Сколько всего кошек в комнате?
. Сколько квадратов на чертеже?

2. Сколько треугольников на чертеже?

. У меня в левом кармане столько же денег, сколько в правом. Из левого переложили в правый одну копейку. На сколько после этого станет больше денег в правом кармане, чем в левом?
. Пять рыбаков за 5 часов распотрошат 5 судаков. За сколько часов 100 рыбаков распотрошат 100 судаков?
. Что тяжелее: пуд железа или пуд пуха?
. На озере росли лилии. Каждый день их число удваивалось и на 20-й день заросло все озеро. На какой день заросла половина озера?
. Разделить фигуру на две равные части

. Четыре человека обменялись рукопожатиями. Сколько всего было рукопожатий?
. Во сколько раз уменьшится число, если от него отнять половину такого же числа?
Математическую викторину можно провести в форме «Ромашки». Для этого надо:
. Изготовить круг из цветной плотной бумаги
. К кругу скрепками прикрепляются разноцветные лепестки, на обратной стороне которых пишется задача
. Ученик из команды подходит к учителю, вытаскивает лепесток, читает и решает задачу

Задачи на лепестках
. У Андрея и Бори вместе 11 орехов. У Андрея и Вовы - 12 орехов. У Бори и Вовы - 13 орехов. Сколько всего орехов у Андрея, Бори и Вовы вместе?
. Из чисел 21, 19, 30, 25, 3, 12, 8, 15, 6, 27 подбери такие три числа, сумма которых равна 50..
. Перечислить не менее 6 способов, которыми можно набрать 15 копеек.
. Как тремя отрезками, не отрывая карандаша от бумаги, перечеркнуть все точки?

. В семье у каждого из 6 братьев есть по сестре. Сколько детей в семье?
. Два в квадрате 4, 3 в квадрате 9. Чему равен угол в квадрате?
. Величина угла 30°. Чему она будет равна, если рассматривать угол в лупу с 2-кратным увеличением?
. Сколькими нулями оканчивается произведение первых десяти натуральных чисел?
. Кто изображен на портрете;
В семье я рос один на свете,
И это правда, до конца.
Но сын того, кто на портрете,-
Сын моего отца
(На портрете - мой отец)
. Найти сумму натуральных чисел от 1 до 100
Учитель может задать по вопросу каждой команде
. Шел Кондрат в Ленинград.
А навстречу 12 ребят.
У каждого по 3 лукошка.
В каждом лукошке кошка.
У каждой кошки 12 котят.
У каждого котенка в зубах по 3 мышонка.
И задумался старый Кондрат:
"Сколько мышат и котят
Ребята несут в Ленинград?"
После ответа учащихся учитель прочитает стихотворение:
"Глупый, глупый Кондрат
Он один шагал в Ленинград,
А ребята с лукошками,
С мышами и кошками
Шли навстречу ему - в Кострому!
. Электропоезд идет с востока на запад со скоростью 60 км/ч. В этом же направлении с востока на запад дует ветер со скоростью 50 км/ч. В какую сторону отклоняется дым поезда?
(Ответ: электропоезд бездымен)
Дидактические игры
Дидактические игры можно использовать как нетрадиционную форму обучения. Основное обучающее воздействие, принадлежит дидактическому материалу, игровым действиям, которые автоматически ведут учебный процесс, направляя активность детей в определенное русло.
Игровая форма занятий создается на уроках при помощи игровых приемов и ситуаций, которые выступают как средство побуждения, стимулирующие учащихся к деятельности.
Реализация игровых приемов и ситуаций при урочной форме занятий проходит по следующим основным направлениям: дидактическая цель ставится перед учащимися в форме игровой задачи; учебная деятельность учащихся подчиняется правилам игры; учебный материал используется в качестве средства игры; в учебную деятельность вводится элемент соревнования, который переводит дидактическую задачу в игровую; успешность выполнения дидактического задания связывается с игровым результатом.
В процессе игры у детей вырабатывается привычка сосредотачиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись, дети не замечают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из детей включаются в игру с огромным желанием, прилагая все усилия, чтобы не подвести товарищей по игре.
Во время игры Деи очень внимательны, сосредоточены и дисциплинированны.
В термине «дидактическая игра» подчеркивается ее педагогическая направленность, отображается многообразие применений. Поэтому есть основания утверждать, что использование дидактической игры в системе обучения математике в 5-11 классах является важным средством интенсификации учебной деятельности школьников, осуществление преемственности между обучением в различных классах.
Дальше рассмотрим некоторые пути и формы использования дидактических игр и игровых ситуаций на уроках математики.
Уроки математики с применением дидактических игр.
Рассмотрим на конкретных примерах организационную и содержательную стороны построения уроков математики, содержащих элементы игры как форму взаимодействия учителя с учащимися, в процессе которой через систему игровых действий реализуются учебно-воспитательные возможности, заложенные в содержании учебного материала.
Алгебра, IX класс.
Тема: «Определение арифметической и геометрической прогрессий».
Цель урока: усвоение учащимися понятий арифметической и геометрической прогрессий.
Оборудование: кодоскоп, диапозитивы, содержащие дидактический материал (количество заданий четное, поровну для I и II команд), указка.
На доске написано:
I команда II команда
Ниже ведется запись полученных очков.
Правила игры.
) Класс разбивается на две команды:
I команда - ученики первого ряда и половины второго ряда;
II команда - ученики третьего ряда и половины второго ряда.
) Выбираются капитаны команд.
) Капитаны команд назначают консультантов. Они должны помогать школьникам из другой команды отвечать на вопросы, предложенные учителем в ходе урока. Их работа приносит дополнительные очки своей команде. Плохо проведенная консультация или отказ от проведения консультации наказывается очками в пользу команды противника.
) После слов «Консультация окончена» школьники занимают свои места. В противном случае команда наказывается штрафными очками.
) Для участия во всех видах работы ученики вызываются к доске капитанами команд.
Ход урока
I этап - консультация. Актуализируются знания учащихся по таким вопросам: определение последовательности, возрастающие и убывающие последовательности, способы задания числовых последовательностей, рекуррентный способ задания последовательности, построение графика последовательности, среднее арифметическое и среднее геометрическое двух чисел.
На консультацию отводится 10-12 минут. Консультируют учеников представители других команд. Разрешаются и взаимоконсультации.

При необходимости консультирует учитель. За консультации команды получают очки.
II этап - учебно-познавательная работа учащихся по самостоятельному приобретению новых знаний.
Предлагается разделить страницу тетради на две части и слева написать «Арифметическая прогрессия», а справа - «Геометрическая прогрессия». На доску (слева) проецируется задача, приводящая к арифметической, а справа - к геометрической прогрессии. К ним проецируются вопросы и задания, которые необходимо выполнить.
Задача 1. Вертикальные стержни фермы имеют такую длину: наименьший а=5дм, а каждый следующий на 2дм длиннее. Записать длину семи стержней. (рис.57)
Задача 2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Записать колонию, рожденную одной бактерией за 7 мин (рис. 58).
) Записать последовательность в соответствии с условием задачи.
) Записать эту же последовательность с помощью таблицы.
) Найти разность d между предыдущим и последующим членами последовательности в первой задаче и частное q от деления последующего члена на предыдущий во второй задаче.
) Задать эти последовательности рекуррентным способом.
) Дать определение арифметической (геометрической) прогрессии.
) Найти среднее арифметическое (геометрическое) чисел 2 и 8. Записать найденное число с данными в порядке возрастания. Образуют ли эти числа арифметическую (геометрическую) прогрессию?
) Справедлива ли такая зависимость для трех последовательных членов рассматриваемых последовательностей?
) Доказать, что для членов арифметической прогрессии справедлива закономерность аn+1=(an+an+2)/2, а для членов геометрической прогрессии закономерность bn+1=√bn*bn+2
Сначала школьники проделывают всю работу на доске и в тетрадях для арифметической прогрессии, а потом - для геометрической или для обеих сразу.
Записи ответов учащихся, которые поочередно вызываются к доске от каждой команды:

В процессе игры учащиеся следят за ответами товарищей, записывают все в тетради и готовятся ответить на предложенный вопрос. Учитель предлагает вопрос, а капитаны команд называют для ответов учащихся из других команд. Подводятся итоги первых двух этапов игры.
III этап - работа школьников по решению упражнений и самостоятельному составлению задач, приводящих к записи арифметической и геометрической прогрессией. За образец взять задачи № 380, 401*.
Решить упражнения:
I команда II команда
№ 433 (а), № 433 (б),
(а) 446 (б)
IV этап - подведение итогов работы. Выигравшая команда объявляется победительницей, а многие учащиеся получают оценку. Задание на дом.
Выводы по 2 главе
Таким образом, развивающий и воспитывающий потенциал
нетрадиционных форм урока можно охарактеризовать с помощью определения следующих целей обучения:
формирование у учащихся интереса и уважения к предмету
воспитание культуры общения и потребности в практическом использовании знаний;
развитие интеллектуальных и познавательных способностей, развитие ценностных ориентаций, чувств и эмоций ученика.
дидактический игра учебный викторина
Заключение
Деятельность учащихся по усвоению содержания образования осуществляется в разнообразных формах обучения, характер которых обусловлен различными факторами: целями и задачами обучения; количеством учащихся, охваченных обучением; особенностями отдельных учебных процессов; местом и временем учебной работы учащихся; обеспеченностью учебниками и учебными пособиями и др.
Процесс обучения реализуется только через организационные формы, которые выполняют интегративную роль, обеспечивая объединение и взаимодействие всех его компонентов. Совокупность форм, объединенных по признаку связи учащихся и учителя посредством учебного материала и дополняющих друг друга, составляет организационную систему обучения.
Организационные формы и системы обучения историчны: рождаются, развиваются, заменяются одна другой в зависимости от уровня развития общества, производства, науки и образовательной теории и практики.
В соответствии с первой задачей были рассмотрены виды нетрадиционных форм уроков, в ходе которых учащиеся расширяют знания, что позволяет учащимся принимать активное участие в обсуждении. Нетрадиционные формы проведения уроков дают возможность не только поднять интерес учащихся к изучаемому предмету, но и развивать их творческую самостоятельность, обучать работе с различными источниками знаний. Такие формы проведения занятий «снимают» традиционность урока, оживляют мысль
В соответствии со второй задачей в моей курсовой работе рассмотрены нетрадиционные формы обучения. Это учебные викторины, урок-практикум, урок-мастерская, дидактические игры. Их использование повышает интерес учащихся к предмету, развивает учебную деятельность школьников. Таким образом, развивающий и воспитывающий потенциал нетрадиционных форм урока можно охарактеризовать с помощью определения следующих целей обучения:
формирование у учащихся интереса и уважения к предмету
воспитание культуры общения и потребности в практическом использовании знаний;
развитие интеллектуальных и познавательных способностей, развитие ценностных ориентаций, чувств и эмоций ученика.
Список используемой литературы
1. Бордовская Н. В., Реан А. А. Педагогика. Учебник для вузов. - СПб: Питир, 2001.
2. Дегтярева З.А. Математика после уроков. - Краснодар, 1996
. Дьяченко В. К. Коллективная структура учебного процесса и ее развитие. - М., 1989.
. Ильина Т. А. Педагогика. - М.: Просвещение, 1984.
. Коваленко В.Г. Дидактические игры на уроках математики. - М., 1990.
. Лихачев Б. Т. Педагогика. Курс лекций. - М.: Прометей, Юрайт, 1998.
. Маквелов С.Г., Маквелова О.Н. Основы конструирования урока. - Армавир, 1993.
. Махмутов М.И. Современный урок. - М. 1981.
. Минекин Е.М. От игры к знаниям. - М., 1987.
. Мухина С.А. Соловьева А.А. Нетрадиционные педагогические технологии в обучении. - Р.-н-Д., 2004.
. Организационные формы обучения./ Под ред. Ю. А. Малеванного. - Киев, 1991.
. Педагогика./ Под ред. В. А. Сластенина. - М.: Академия, 2004.
. Педагогика./ Под ред. П. И. Пидкаситого. - М., 2002.
. Педагогика./ Под ред. Ю. К. Бабанского. - М.: Просвещение,1998.
. Савин Н. В. Педагогика. - М.: Просвещение, 1972.
. Скакин М.Н. Проблемы современной дидактики. - М., 1990.
. Сластенин В. А., Исаев И. Ф., Шиянов Е. Н. Общая педагогика. - М.: Владос, 2003.
. Теоретико - методологические основы учебно - воспитательного процесса в школе и вузе. Сборник научных трудов. - Волгоград, 1984.
. Харламов И. Ф. Как активизировать учение школьников. - М., 1975.
. Харламов И. Ф. Педагогика. - Минск, 2002.
|
|
|


