Лабораторная работа №1 - Развитие съёмочного обоснования.

1.1 Исходные данные. Съемочным обоснованием называют систему достаточно точно определенных геодезических пунктов, создаваемых в необходимом и достаточном количестве на рабочих горизонтах карьера для съемки подробностей.

"Техническая инструкция..." рекомендует применять следующие вида съемочного обоснования: аналитические сети, геодезические засечки, теодолитные хода, прямоугольные сетки, профильные линии.

Тип съемочного обоснования (значит и способ его создания) зависят от рельефа местности, расположения рабочих горизонтов относительно господствующего горизонта земной поверхности, раз­меров и конфигурации карьера и системы ведения горных работ.

Наиболее универсальной и часто используемой из вышеперечисленных способов являются геодезические засечки: прямая и обратная.

Исходные данные:

Пункты опорной сети на местности с известными координатами:

 

- А (X = 0,000 м, У =0,000 м);

- В (X = 0,000 м, У =50,000 м);

У изменяется от 35, 000 до 50, 000м ч-з 1м в зависимости от варианта

- С (X =43,302 м, У =25,000 м);

Требуется:

1) Произвести сгущение геодезической сети пунктом съемочно­го обоснования способами прямой и обратной геодезической засечки;

2) Определить координаты пункта Д двумя способами.

 

1.2 Прямая геодезическая засечка применяется для определения коор­динат дополнительной точки на основании двух исходных пунктов с из­вестными координатами на местности, неудобной для производства ли­нейных измерений. При этом способе измеряют все три угла (b_А, b_В, b_Д) треугольника. Углы при определяемом пункте не должно быть мень­ше 30° ибольше 120°. Угловая невязка в треугольнике не должна пре­вышать 45^//- 60".

Решение задачи выполняется в следующей последовательности:

I.2.I Нанести на бумагу в масштабе 1:500 по координатам точки А и В. Произвольно нанести положение пункта Д, В треугольнике АВД находят угловую невязку, распределяют ее поровну на все измеренные углы с обратным знаком и получают ис­правленные значения b^/_А, b^/_В, b^/_Д:

f_b = (b_А, b_В, b_Д) – 180⁰, b^/_А = b_А + ,

b^/_В = b_В + , b^/_Д = b_Д + .

1.2.2 Определяют дирекционный угол стороны АВ(a_{А В})и её горизонтальную длину d_AB

Рис.1.1

 

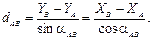
1.2.3 По теорию синусов вычисляют длины других сторон треугольника через известную длину стороны АВ и измеренные углы.

 

,

 

1.2.4 Находят дирекционные углы сторон АД и ВД

 

a_АД=a_АВ - b^/_А, a_ВД= a_ВА + b^/_В,

где a_ВА= a_АВ± 180⁰.

1.2.5 Вычисляют приращения координат точки Д относительно точки А и относительно точки В

 

DХ_АД=d_АД×cosa_АД DХ_ВД=d_ВД×cosa_ВД

DУ_АД=d_АД×sina_АД DУ_ВД=d_ВД×sina_ВД

I.2.6 Вычисляют координаты точки Д дважды:

относительно точки А относительно точка В

Х_Д=Х_А+DХ_АД Х_Д=Х_В+DХ_ВД

У_Д=У_А+DУ_АД У_Д=У_В+DУ_ВД

 

Двойное значение найденных координат точки Д дают контроль вычислений.

 

1.3 Обратная геодезическая засечка заключается в определении координат дополнительной точки Д (рисунок 1.2) путем измерения на этой точке углов (a, b) между направлениями на три данных пункта (А, В, С) и более, с известными координатами.

Решение задачи выполняется в следующей последовательности:

I.3.I По известным координатам пунктов А(Х_А, У_А), B(X_В,У_В), C(X_С,У_С) находят дирекционные угли сторон АВ и ВС их горизонтальные длины:

 

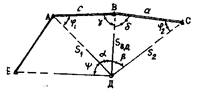
Рисунок 1.2

 

 

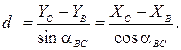
1.3.2 Вычисляют значение угла ABC:

 

ÐАВС = g + d = a_ВА-a_ВС.

 

1.3.3 Определяют горизонтальные углы j₁ и j₂ при исход­ных пунктах А и С, для чего:

1.3.3.1 Находят сумму углов j₁ и j₂

 

j₁ + j₂ = 360⁰ – (g + d)-(a + b).

 

1.3.3.2. Определяют разность углов j₁ и j₂.

Для этого из треугольников АВД и СВД составля­ют соотношение

 

 

Введя обозначения = ctgq находят значение вспомогательного угла q. Исходя из формулы

определяют полуразность углов j₁ - j₂/2.

1.3.3.3 Зная полусумму и полуразность углов, находят значение углов j₁ и j₂

 

 

1.3.4 Из треугольников ВАД и ВСД определяют углы g и d:

 

g =180⁰-j₁-a; d = 180⁰- j₂ - b

Контроль: g + d = ÐABC.

 

1.3.5 Находят дирекционные углы a_АД, a_СД и горизонтальные длины этих сторон

 

a_АД= a_АВ + j₁, a_СД= a_СВ - j₂

 

 

1.3.6 Вычисляют приращение координат точки Д:

 

относительно точки А: относительно точки С:

DХ_АД=S₁×cosa_АД; DХ_СД=S₂×cosa_CД;

DУ_АД=S₁×sina_АД; DY_СД= S₂×sina_CД;

1.3.7 Определяют координаты точки Д дважды:

относительно точки А: относительно точки С:

Х_Д = Х_А + DХ_АД; Х_Д = Х_С + DХ_СД;

У_Д = У_А + DУ_АД; У_Д = У_С + DУ_СД.

Двойное значение найденных координат точки Д даст кон­троль вычислений.

Следует иметь в виду, что обратная засечка не может быть вычислена, если три исходных пункта и определяемая точка лежат на одной окружности. В этом случае обратная засечка должна осу­ществляться не по трем, а по четырем исходным пунктам.

Кроме классического способа Потенота существует много раз­ных способов решения обратной засечки по формулам Кнейссля, Коллинса, И.Ю.Пранис-Праневича, Ф.Ф.Павлова, Ансермета и др.

Литература: Осн. 2 [cтр. 3 - 6]

Контрольные вопросы:

1. Сколько необходимо пунктов для решения прямой геодезической засечки?

2. Сколько необходимо исходных пунктов для решения обратной геодезической засечки?

3. Перечислите способы решения обратной геодезической засечки.

4. От чего зависит тип съёмочного обоснования?

5. В каком случае обратная засечка должна осу­ществляться не по трем, а по четырем исходным пунктам?

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: