 |
Преобразуем структурную алгоритмическую схему.
|
|
|
|
Пояснительная записка
По курсовой работе
“Теория Автоматического Регулирования”
Вариант 9
Выполнили студенты:
группы 3023/2
Сибирко А. С.
Преподаватель:
Попков Е.Н.
Санкт-Петербург
Материалы к учебной работе по курсу
"Теория автоматического регулирования"
Цель работы
1. Исследование системы электропитания с регулируемым источником.
2. Оптимизация параметров системы электропитания с целью повышения качества регулирования и улучшения характеристик переходных процессов и стационарных режимов.
Описание системы
Принципиальная схема системы электропитания приведена на рис.1. Ее образуют:
- основной источник Е0;
- регулируемый источник Ер;
- датчик Д текущего значения регулируемой переменной;
- регулятор Р с уставкой Хуст номинального значения регулируемой переменной;

|
- исполнительный механизм ИМ, обеспечивающий изменение э.д.с. Ер.
Эквивалентная схема замещения нагрузки приведена на рис.2. Регулируемой переменной является ток i катушки индуктивности L.
Параметры нагрузки: R0=1.8 кОм, R = 0.6 кОм, С = 110 мкФ.

Рис 2.
Для элементов цепи регулирования использовать следующие эквиваленты:
1) датчик - пропорциональное звено с коэффициентом усиления Кд;
2) регулятор - инерционное звено первого порядка с коэффициентом усиления Кр и постоянной времени Тр;
3) исполнительный механизм - инерционное звено первого порядка с коэффициентом усиления Ким и постоянной времени Тим.
Параметры цепи регулирования: Ким = 2,5, Тим = 0.04 с., Тр = 0.01 с.
Номинальное значение регулируемой переменной в установившемся режиме: 400 В.
Пункт 1.
Представим нагрузку системы питания в виде звена, для которого входным сигналом является напряжение на зажимах источника питания, а выходным сигналом – указанная регулируемая переменная. Получить описание звена в виде сокращённой записи дифференциального уравнения и передаточной функции. Установить тип звена и рассчитать численные значения параметров.
|
|
|

а). Операторное пространство:

б). Физическое пространство:
Составим систему уравнений на основе 1 и 2 законов Кирхгофа



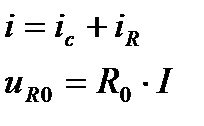
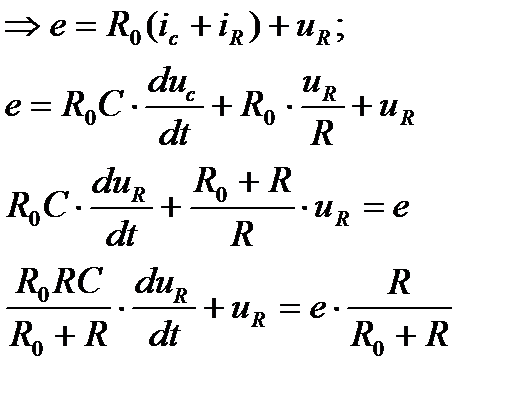
По виду дифференциального уравнения делаем вывод, что данное эквивалентное звено является Апериодическим звеном I-ого порядка (Инерционное звено I-ого порядка)
· Сокращённая запись дифференциального уравнения с учётом исходных данных:
R0=1.8 кОм
R = 0.6 кОм
С = 110 мкФ.
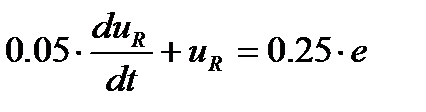
|
(1)
Обозначим в (1) T=0,05 и К=0.25.
Пункт 2.
Рассчитаем величину ЭДС Е0 основного источника необходимого для обеспечения нормального режима работы системы питания.
Разрываем конденсатор и получаем расчетную схему:

Uуст=400 В

б) Определение Е0 основного источника, используя передаточную функцию звена.
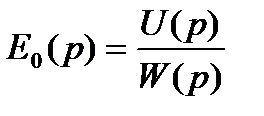

В результате выполнения расчёта двумя способами мы получили одинаковые ответы, следовательно, мы можем считать что расчёты были произведены верно.
Пункт 3.
Построение аналитической переходной характеристики звена, эквивалентирующего нагрузку.


Пункт 4.
Получение на ЭВМ переходной характеристики звена, эквивалентирующего нагрузку. Используем вычислительный комплекс «РИТМ».
1) BLT 103 – источник кусочно-постоянного сигнала
2) BLT 133 – инерционное звено первого порядка
3) BLT 014 – осциллограф
4) BLT 015 – табулятор

Х1-1-входной сигнал звена (единичное ступенчатое воздействие)
Х2-1-сигнал на выходе звена - переходная характеристика звена (реакция звена на единичное ступенчатое воздействие).
Аналитическая переходная характеристика звена и построенная в РИТМе совпадают. В аналитической k= 0.25 в Ритме k=0.25. Погрешность = 0.0
|
|
|

· Определение параметров звена по экспериментальной переходной характеристике:


 (совпадает с аналитическим k=0.25)
(совпадает с аналитическим k=0.25)
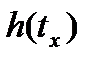 =0.158,
=0.158,  =0.05
=0.05
 =
=  (отличие от аналитического значения составляет 0%)
(отличие от аналитического значения составляет 0%)
Пункт 5.
Выполнение тестового расчета, подтверждающего правильность определения э.д.с. Е0
Вместо источника единичного ступенчатого сигнала включаем в цепь источник с найденным аналитически значением ЭДС (Е0=260В).

Х1- входной сигнал звена
Х2-сигнал на выходе звена
При выполнении тестового расчета было получено значение выходного сигнала, равное 400 B, что не отличается от значения уставки регулируемой величины ( )
)
Пункт 6.
Построение аналитической амплитудно-фазовой частотной характеристики звена, эквивалентирующего нагрузку.


|

|

|

Выберем значения частот, так чтобы точки равномерно расположились на кривой.
· Полученные значения частоты заносим в таблицу
=ω
Пункт 7.
Построение экспериментальной АФЧХ звена, эквивалентирующего нагрузку.
Схема имитационной модели:
1) BLT 091 – генератор гармонического сигнала
2) BLT 133 – инерционное звено первого порядка
3) BLT 014 – осциллограф
4) BLT 015 – табулятор
· Критерий достоверности:


Осциллограмма входного и выходного сигнала при частоте f = 12,732395 Гц

Таблица значений для расчетов, необходимых для построения АФЧХ звена, эквивалентирующего нагрузку:
| ω, рад/с | f,Гц | Т,с | Тнач.гарм.анализа | Ток | h | X | φ,рад | W' | W'' |
| 0.795775 | 1.25663 | 6,283 | 8,168 | 0.001256 | 0.242492 | -0.246 | 0.235 | -0.059 | |
| 1.591549 | 0.6283 | 3,142 | 4,084 | 0.006283 | 0.223653 | -0.463195 | 0.2 | -0.1 | |
| 3.183099 | 0.31416 | 1,571 | 2,042 | 0.003142 | 0.176684 | -0.786 | 0.125 | -0.125 | |
| 6.366198 | 0.1571 | 0,785 | 1,021 | 0.001571 | 0.118 | -1.107 | 0.053 | -0.103 | |
| 12.732395 | 0.07854 | 0,393 | 0,511 | 0.000785 | 0.061 | -1.326 | 0.015 | -0.059 | |
| 25.46479 | 0.03927 | 0,196 | 0,255 | 0.000393 | 0.0309 | -1.433 | 0.0039 | -0.031 | |
| 63.661977 | 0.019635 | 0,098 | 0,128 | 0.000196 | 0.012 | -1.5 | 0.00085 | -0.012 |
 ,
,
 ,
,
Tок=6Т, – время окончания расчета
Тга=(3-5)Т, – время начала гармонического анализа
h=  – шаг расчета. (округляется в меньшую сторону)
– шаг расчета. (округляется в меньшую сторону)

| - Амплитуда -Фаза |
Пример расчёта для 1 строки: 


Значения амплитуды и фазы полученные с помощью программы РИТМ заносятся в Таблицу.
|
|
|
В РИТМе были получены значения для действительной A и мнимой B частей АФЧХ. По этим значениям были выставлены 6 точек, которые лежат на аналитической АФЧХ.

|
Красный цвет – аналитически построенная АФЧХ.
Cиний цвет – экспериментально построенная АФЧХ.
Пункт 8.
Составление структурной алгоритмической схемы САУ.
| Хуст |
| Хуст |
| Wр |
| Е0 |
| Wим |
| Δх |
| Хр |
| Ер |
| Е0 |
| f |
| Wн |
| + |
| Wд |
| – |
| Xуст |
| W3 |
| W4 |
| W7 |
| Eo |
| W8 |
| f |
| X |
| Eр |
Преобразуем структурную алгоритмическую схему.
· Объединяем последовательно соединенные звенья W3,W4 (перемножая их).
| Xуст |
| W3*W4 |
| W7 |
| Eo |
| W8 |
| f |
| X |
· Переносим вперед через сумматор-6 звено с передаточной функцией W3*W4 (это приводит к появлению звена с передаточной функцией обратной к функции обойдённого звена).
| Xуст |
| W3*W4 |
| W7 |
| Eo |
| W8 |
| f |
| X |
| 1/ W3*W4 |
· Объединяем сумматоры 2 и 6. Далее эквивалентируем передаточные функции звеньев W3,W4,W7,W8, объединенных в обратную отрицательную связь, получаем звено W9
| Xуст |
| 1/ W3*W4 |
| W9 |
| Eo |
| f |

4.Эквивалентируем относительно Xуст
| Xуст |
| W9 |
| f |
Получим эквивалентную передаточную функцию.



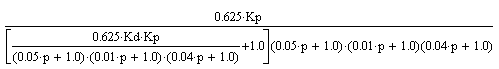
5.Эквивалентируем относительно Eo
| 1/ W3*W4 |
| W9 |
| Eo |
| f |
Получим эквивалентную передаточную функцию.


Пункт 9.
Построить область устойчивости системы в плоскости коэффициентов Кри Кд, где Кр —коэффициент усиления звена, эквивалентирующего регулятор, а Кд — коэффициент усиления звена, эквивалентирующего датчик текущего значения регулируемой переменной.
Полученное значение передаточной функции эквивалентированной структурно – алгоритмической схемы САУ:
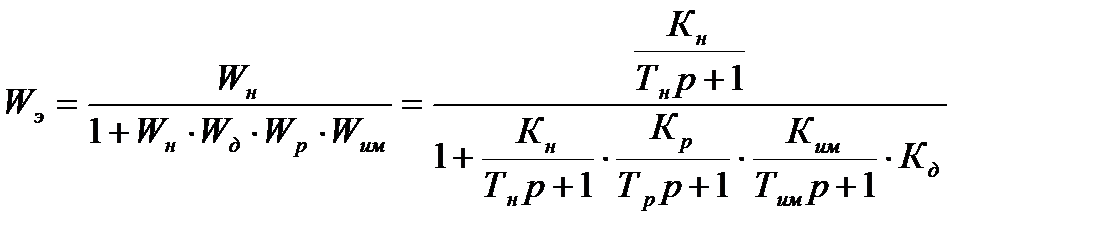
Из знаменателя эквивалентной передаточной функции:

При замене р на 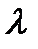 получаем характеристический полином:
получаем характеристический полином:
 ,
,
с коэффициентами

Для определения области устойчивости используем критерий устойчивости Гурвица.
|
|
|
Условие устойчивости заключается в требовании положительности определителя Гурвица и всех его диагональных миноров.
Т.о. условия устойчивости:

Для построения границ областей устойчивости используем следующие уравнения
1. 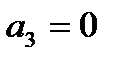
Т.е. 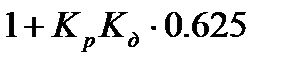 = 0
= 0

2. 

На основе уравнений  и
и  строим области устойчивости относительно неизвестных параметров Кри Кд:
строим области устойчивости относительно неизвестных параметров Кри Кд:

Проверим, какие из этих областей являются устойчивыми. Для этого выберем точку в каждой из областей и воспользуемся критерием Гурвица. Для устойчивости системы необходима и достаточна положительность определителя Гурвица и всех его миноров.
Возьмём точку с координатами: К д = 1 Кр = 1 (область 1)
 Область устойчива
Область устойчива
Возьмём точку с координатами: К д = 10 Кр =-10 (область 2)
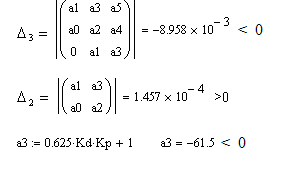 Область неустойчива
Область неустойчива
Возьмём точку с координатами: К д = 15 Кр = 10 (область 3)
 Область неустойчива
Область неустойчива
Возьмём точку с координатами: К д = -5 Кр = 5 (область 4)
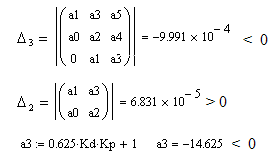 Область неустойчива
Область неустойчива
Возьмём точку с координатами: К д = -15 Кр = -10 (область 5)
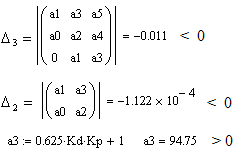 Область неустойчива
Область неустойчива
Область 1 является устойчивой, т.к. выполняются условия устойчивости, а именно положительность определителя Гурвица и всех его диагональных миноров.
Преподавателем были выбраны коэффициенты  из области устойчивости.
из области устойчивости.
Пункт 10.
Далее, после выбора коэффициентов  из области устойчивости, подготовим имитационная модель САУ в программе РИТМ, имеющую следующий вид.
из области устойчивости, подготовим имитационная модель САУ в программе РИТМ, имеющую следующий вид.
1- генератор кусочно-постоянного сигнала 
2- сумматор
коэффициенты сумматора
k = 1, k = -1
3- Регулятор.инерционное звено первого порядка

4- Исполнительный механизм. инерционное звено первого порядка

5- генератор кусочно-постоянного сигнала 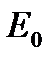 = 1600 В.
= 1600 В.
6- сумматор
коэффициенты сумматора
k = 1,k = 1
7- инерционное звено первого порядка

8- пропорциональное звено
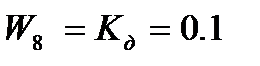
9- осцилограф
10- табулятор
В результате расчета данной имитационной модели был получен график:
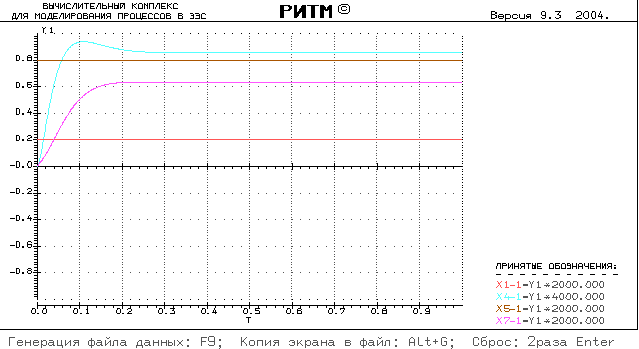
Видно, что при данных настройках системы требуемое условие  = 0 в установившемся режиме не выполняется. Внесем некоторые изменения в настройки системы.
= 0 в установившемся режиме не выполняется. Внесем некоторые изменения в настройки системы.
Пункт 11.
Выбрать значения коэффициентов Кри Кд из области устойчивости, которые в статическом режиме обеспечивают нулевую величину э.д.с. Ер регулируемого источника. По результатам эксперимента рассчитать статизм, перерегулирование и длительность переходного процесса для выбранных значений коэффициентов Кри Кд. Рассчитать теоретические значения указанных показателей.
Для того чтобы в установившемся режиме сумматор, стоящий перед регулятором, давал нулевой сигнал (Δх = 0), необходимо добавить пропорциональное звено с W=Wд
|
|
|
| Е0 |
| Wн |
| Ер |
| Е0 |
| f |
| Wр |
| Δх |
| Хуст |
| Хуст |
| Wкор |
| Wим |
| Хр |
| Wд |
| – |
Δх=Xуст-Х=40-40=0
через регулируемый источник пройдет нулевой сигнал, и, следовательно, получаем  = 0.
= 0.
Переходный процесс включения системы питания при нулевых начальных условиях будет иметь следующий вид.

Пункт 12.
Подготовить имитационную модель, позволяющую за один расчет выполнить:
— моделирование процесса включения системы питания с получением установившегося режима;
— моделирование последующего переходного процесса, обусловленного потерей 50% величины э.д.с. Е0с получением нового установившегося режима.

1) Статизм:
эксперимент:
 %
%
расчёт:
Для расчета величины статизма необходимо положить в выражении для эквивалентной передаточной функции р = 0: δ = W э(0)

2) Перерегулирование:
эксперимент:
из графика  %
%
расчёт:
Характеристический полином равен:

Получились корни:  ,
, 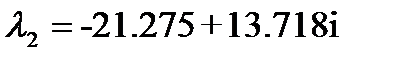 ,
,  .
.
 ,
, 

 %
%
3) Длительность переходного процесса:
из графика:
 сек
сек
Расчёт:
время переходного процесса определяется как 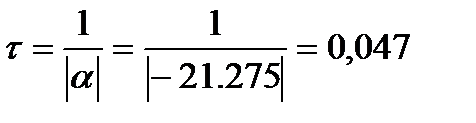
длительность переходного процесса  сек
сек
Пункт 13.
Провести поэтапную оптимизацию коэффициентов Кри Кдс целью обеспечения допусти-мых значений показателей качества.
Допустимые значения показателей качества:
Статизм: δдоп = 5%
Перерегулирование: σдоп = 30%
Проведём расчёт для Кр так чтобы статизм был в пределах допуска.
Для этого приравняем передаточную функцию еквивалентированную относительно Ео(при р=0)

выразим отсюда Кд: 

1) Статизм:
эксперимент:
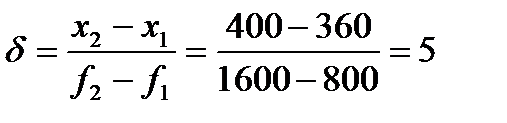 %
%
2) Перерегулирование:
эксперимент:
из графика  20%
20%
3) Длительность переходного процесса:
из графика:
 сек
сек
Пункт 14.
Увеличить быстродействие системы не менее, чем в два раза, не допуская при этом, чтобы напряжение на нагрузке превосходило двукратное значение 100% э.д.с. основного источника.
Для увеличения быстродействия системы скомпенсируем самую медленную составляющую системы. Самой медленной составляющей системы является постоянная времени исполнительного механизма  с.
с.
Для ускорения процесса выберем гибкую обратную связь. Охватим звено исполнительного механизма отрицательной обратной связью с реальным дифференцирующим звеном.


1) Статизм:
эксперимент:
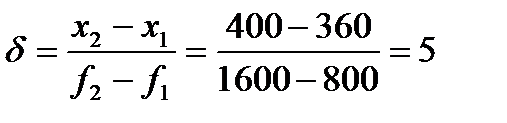 %
%
2) Перерегулирование:
эксперимент:
из графика  20%
20%
3) Длительность переходного процесса:
из графика:
 с
с
Вывод:
Целью данной курсовой работы было исследование системы электропитания с регулируемым источником и оптимизация параметров системы электропитания с целью повышения качества регулирования и улучшения характеристик переходных процессов и стационарных режимов. В ходе выполнения курсовой работы мы разработали систему автоматического регулирования, позволяющую при потере э.д.с. основного источника на 50% сохранять свою работоспособность. Показатели качества переходного процесса удовлетворяют допустимым значениям статизм (5%), перерегулирование (30%). По заданию преподавателя, мы ускорили быстродействие нашей системы с помощью введения корректирующего звена (реального дифференцирующего). Так же получили максимальное значение напряжения) на нагрузке, не превышающее двукратного значения Е0=3200В, а значит изоляция нашей системы выдержит напряжение на нагрузке. Таким образом проведенные мероприятия привели к полной работоспособности нашей системы.
|
|
|


