 |
Результаты работы программы для обнаружения границ фаз в термическом анализаторе алюминиевых сплавов при помощи нечеткой логики.
|
|
|
|
Результаты работы программы для разных участков кривой представлены на рисунках 7.6-7.10.


Рисунок 7.6 – Участок кривой №11 Рисунок 7.7 – Участок кривой №12


Рисунок 7.8 – Участок кривой №13 Рисунок 7.10 – Участок кривой № 40

Рисунок 7.9 – Участок кривой № 39
Файл-сценарий для создания СНВ и сохранения ее на диске в виде файла
Используя данные о диапазоне изменения значений входных и выходных параметров, границы и тип ФП, правила, веса правил и метод дефазификации, изложенные в п. 1.4, пишем программу в виде файла-сценария для создания СНВ и сохранения ее на диске в виде файла.
script;
k = 1+0.15;
k1 = 1+0.05;
a = newfis('Fis_lab_fz');
a = addvar(a,'input','L1',[0 0.0065]);
a=addmf(a,'input',1,'small','trapmf',[0 0 0.00009*k*(1+0.035) 0.00011*k*(1+0.035)]);
a=addmf(a,'input',1,'mid_left','trimf',[0.00009*k1*(1+0.035) 0.000295*k1*(1+0.035) 0.0005*k1*(1+0.035)]);
a=addmf(a,'input',1,'mid_rig','trimf',[0.0004*k*(1+0.035) 0.0007*k*(1+0.035) 0.001*k*(1+0.035)]);
a=addmf(a,'input',1,'big','trapmf',[(0.0008-0.0005)/2+0.0005+0.00005*k*(1+0.035) 0.001*k*(1+0.035) 0.0055 0.0055]);
plotmf(a,'input',1);
k2 = 1+0.15;
k3 = 1+0.05;
a = addvar(a,'input','L2',[0 0.012]);
a = addmf(a,'input',2,'small','trapmf',[0 0 0.00015*k2 0.00025*k]);
a = addmf(a,'input',2,'middle','trimf',[0.00015*k3 0.000575*k3 0.001*k3]);
a = addmf(a,'input',2,'big','trapmf',[0.0008*k2 0.001*k2 0.012 0.012]);
figure;
plotmf(a,'input',2);
k4 = 1+0.1;
k5 = 1+0.2;
a = addvar(a,'input','t1',[0 90]);
a= ddmf(a,'input',3,'small','trapmf',[0 0 3*k4*(1+0.05) 6.5*k4*(1+0.05)]);
a=addmf(a,'input',3,'big','trapmf',[3*k5*(1+0.05) 6.5*k5*(1+0.05) 90 90]);
figure;
plotmf(a,'input',3);
k5 = 1+0.05;
k6 = 1+0.1;
a = addvar(a,'input','t2',[0 90]);
a=addmf(a,'input',4,'small','trapmf',[0 0 30*k5*(1+0.05) 32*k5*(1+0.05)]);
a=addmf(a,'input',4,'big','trapmf',[30*k6*(1+0.05) 32*k6*(1+0.05) 90 90]);
figure;
plotmf(a,'input',4);
k7 = 1-0.005;
a = addvar(a,'input','location',[0 260]);
a = addmf(a,'input',5,'left','trapmf',[0 0 80 85]);%it was 70 80
a = addmf(a,'input',5,'right','trapmf',[80 85 260 260]);
figure;
plotmf(a,'input',5);
a = addvar(a,'output','decision',[0 1]);
a = addmf(a,'output',1,'No','trapmf',[0 0 0.4 0.6]);
a = addmf(a,'output',1,'Yes','trapmf',[0.4 0.6 1 1]);
figure;
plotmf(a,'output',1);
ruleList = [ 1 1 1 1 1 1 0.9 1;...
1 1 1 2 1 1 0.9 1;...
1 1 2 1 1 1 0.9 1;...
1 1 2 2 1 1 0.9 1;...
1 1 1 1 2 1 0.9 1;...
1 1 1 2 2 1 0.9 1;...
|
|
|
1 1 2 1 2 1 0.9 1;...
1 1 2 2 2 1 0.9 1;...
1 2 1 1 1 1 0.9 1;...
1 2 1 2 1 1 0.9 1;...
1 2 2 1 1 1 0.9 1;...
1 2 2 2 1 1 0.9 1;...
1 2 1 1 2 1 0.9 1;...
1 2 1 2 2 1 0.9 1;...
1 2 2 1 2 1 0.9 1;...
1 2 2 2 2 1 0.9 1;...
1 3 1 1 1 1 0.9 1;...
1 3 1 2 1 1 0.9 1;...
1 3 2 1 1 1 1 1;...
1 3 2 2 1 1 0.9 1;...
1 3 1 1 2 1 0.9 1;...
1 3 1 2 2 1 0.9 1;...
1 3 2 1 2 1 1 1;...
1 3 2 2 2 2 0.9 1;...
2 1 1 1 1 1 0.9 1;...
2 1 1 2 1 1 0.9 1;...
2 1 2 1 1 1 0.6 1;...
2 1 2 2 1 1 0.9 1;...
2 1 1 1 2 1 0.9 1;...
2 1 1 2 2 1 0.9 1;...
2 1 2 1 2 1 0.6 1;...
2 1 2 2 2 1 0.9 1;...
2 2 1 1 1 1 0.9 1;...
2 2 1 2 1 1 0.9 1;...
2 2 2 1 1 1 1 1;...
2 2 2 2 1 1 1 1;...
2 2 1 1 2 1 0.9 1;...
2 2 1 2 2 1 0.9 1;...
2 2 2 1 2 1 1 1;...
2 2 2 2 2 1 1 1;...
2 3 1 1 1 1 0.7 1;...
2 3 1 2 1 1 1 1;...
2 3 2 1 1 1 1 1;...
2 3 2 2 1 1 1 1;...
2 3 1 1 2 1 0.7 1;...
2 3 1 2 2 1 1 1;...
2 3 2 1 2 2 1 1;...
2 3 2 2 2 2 1 1;...
3 1 1 1 1 1 0.9 1;...
3 1 1 2 1 1 0.9 1;...
3 1 2 1 1 1 0.6 1;...
3 1 2 2 1 1 0.9 1;...
3 1 1 1 2 1 0.9 1;...
3 1 1 2 2 1 0.9 1;...
3 1 2 1 2 2 0.2 1;...
3 1 2 2 2 1 0.9 1;...
3 2 1 1 1 1 1 1;...
3 2 1 2 1 1 1 1;...
3 2 2 1 1 1 0.5 1;...
3 2 2 2 1 1 1 1;...
3 2 1 1 2 1 1 1;...
3 2 1 2 2 1 1 1;...
3 2 2 1 2 1 0.5 1;...
3 2 2 2 2 1 1 1;...
3 3 1 1 1 1 0.7 1;...
3 3 1 2 1 1 1 1;...
3 3 2 1 1 1 1 1;...
3 3 2 2 1 1 1 1;...
3 3 1 1 2 1 0.7 1;...
3 3 1 2 2 1 1 1;...
3 3 2 1 2 1 1 1;...
3 3 2 2 2 2 1 1;...
4 1 1 1 1 1 0.9 1;...
4 1 1 2 1 1 0.9 1;...
4 1 2 1 1 1 1 1;...
4 1 2 2 1 1 0.9 1;...
4 1 1 1 2 1 0.9 1;...
4 1 1 2 2 1 0.9 1;...
4 1 2 1 2 1 1 1;...
4 1 2 2 2 1 0.9 1;...
4 2 1 1 1 1 0.9 1;...
4 2 1 2 1 1 1 1;...
4 2 2 1 1 1 1 1;...
4 2 2 2 1 1 1 1;...
4 2 1 1 2 1 0.9 1;...
4 2 1 2 2 1 1 1;...
4 2 2 1 2 2 1 1;...
4 2 2 2 2 2 1 1;...
4 3 1 1 1 1 0.9 1;...
4 3 1 2 1 1 1 1;...
4 3 2 1 1 2 1 1;...
4 3 2 2 1 1 1 1;
4 3 1 1 2 1 0.9 1;...
4 3 1 2 2 1 1 1;...
4 3 2 1 2 2 1 1;...
4 3 2 2 2 2 1 1];
a = addrule(a,ruleList);
a = setfis(a,'DefuzzMethod','mom');
fuzzy(a)
showfis(a); %анотация к системе
writefis(a,'fis_lab_fz'); %запись системы на диск
Аннотация к созданной СНВ
fis_laba3
1. Name termX_mix_last_mom
2. Type mamdani
3. Inputs/Outputs [5 1]
4. NumInputMFs [4 3 2 2 2]
5. NumOutputMFs 2
6. NumRules 96
7. AndMethod min
8. OrMethod max
9. ImpMethod min
10. AggMethod max
11. DefuzzMethod centroid
12. InLabels L1
13. L2
14. t1
15. t2
16. loc
17. OutLabels decis
18. InRange [0 0.0065]
19. [0 0.012]
20. [0 90]
21. [0 90]
22. [0 260]
23. OutRange [0 1]
24. InMFLabels small
25. mid_left
26. mid_rig
27. big
28. small
29. middle
30. big
31. small
32. big
33. small
34. big
35. left
36. right
37. OutMFLabels No
38. Yes
39. InMFTypes trapmf
40. trimf
41. trimf
42. trapmf
43. trapmf
44. trimf
45. trapmf
46. trapmf
47. trapmf
48. trapmf
49. trapmf
50. trapmf
51. trapmf
52. OutMFTypes trapmf
53. trapmf
54. InMFParams [0 0 0.0001071 0.0001309]
55. [9.781e-005 0.0003206 0.0005434 0]
56. [0.0004761 0.0008332 0.00119 0]
57. [0.0007095 0.00119 0.0055 0.0055]
58. [0 0 0.0001725 0.0002875]
|
|
|
59. [0.0001575 0.0006038 0.00105 0]
60. [0.00092 0.00115 0.012 0.012]
61. [0 0 3.465 7.508]
62. [3.78 8.19 90 90]
63. [0 0 33.08 35.28]
64. [34.65 36.96 90 90]
65. [0 0 80 85]
66. [80 85 260 260]
67. OutMFParams [0 0 0.4 0.6]
68. [0.4 0.6 1 1]
69. Rule Antecedent [1 1 1 1 1]
70. [1 1 1 2 1]
71. [1 1 2 1 1]
72. [1 1 2 2 1]
73. [1 1 1 1 2]
74. [1 1 1 2 2]
75. [1 1 2 1 2]
76. [1 1 2 2 2]
77. [1 2 1 1 1]
78. [1 2 1 2 1]
79. [1 2 2 1 1]
80. [1 2 2 2 1]
81. [1 2 1 1 2]
82. [1 2 1 2 2]
83. [1 2 2 1 2]
84. [1 2 2 2 2]
85. [1 3 1 1 1]
86. [1 3 1 2 1]
87. [1 3 2 1 1]
88. [1 3 2 2 1]
89. [1 3 1 1 2]
90. [1 3 1 2 2]
91. [1 3 2 1 2]
92. [1 3 2 2 2]
93. [2 1 1 1 1]
94. [2 1 1 2 1]
95. [2 1 2 1 1]
96. [2 1 2 2 1]
97. [2 1 1 1 2]
98. [2 1 1 2 2]
99. [2 1 2 1 2]
100. [2 1 2 2 2]
101. [2 2 1 1 1]
102. [2 2 1 2 1]
103. [2 2 2 1 1]
104. [2 2 2 2 1]
105. [2 2 1 1 2]
106. [2 2 1 2 2]
107. [2 2 2 1 2]
108. [2 2 2 2 2]
109. [2 3 1 1 1]
110. [2 3 1 2 1]
111. [2 3 2 1 1]
112. [2 3 2 2 1]
113. [2 3 1 1 2]
114. [2 3 1 2 2]
115. [2 3 2 1 2]
116. [2 3 2 2 2]
117. [3 1 1 1 1]
118. [3 1 1 2 1]
119. [3 1 2 1 1]
120. [3 1 2 2 1]
121. [3 1 1 1 2]
122. [3 1 1 2 2]
123. [3 1 2 1 2]
124. [3 1 2 2 2]
125. [3 2 1 1 1]
126. [3 2 1 2 1]
127. [3 2 2 1 1]
128. [3 2 2 2 1]
129. [3 2 1 1 2]
130. [3 2 1 2 2]
131. [3 2 2 1 2]
132. [3 2 2 2 2]
133. [3 3 1 1 1]
134. [3 3 1 2 1]
135. [3 3 2 1 1]
136. [3 3 2 2 1]
137. [3 3 1 1 2]
138. [3 3 1 2 2]
139. [3 3 2 1 2]
140. [3 3 2 2 2]
141. [4 1 1 1 1]
142. [4 1 1 2 1]
143. [4 1 2 1 1]
144. [4 1 2 2 1]
145. [4 1 1 1 2]
146. [4 1 1 2 2]
147. [4 1 2 1 2]
148. [4 1 2 2 2]
149. [4 2 1 1 1]
150. [4 2 1 2 1]
151. [4 2 2 1 1]
152. [4 2 2 2 1]
153. [4 2 1 1 2]
154. [4 2 1 2 2]
155. [4 2 2 1 2]
156. [4 2 2 2 2]
157. [4 3 1 1 1]
158. [4 3 1 2 1]
159. [4 3 2 1 1]
160. [4 3 2 2 1]
161. [4 3 1 1 2]
162. [4 3 1 2 2]
163. [4 3 2 1 2]
164. [4 3 2 2 2]
69. Rule Consequent 1
70. 1
71. 1
72. 1
73. 1
74. 1
75. 1
76. 1
77. 1
78. 1
79. 1
80. 1
81. 1
82. 1
83. 1
84. 1
85. 1
86. 1
87. 1
88. 1
89. 1
90. 1
91. 1
92. 2
93. 1
94. 1
95. 1
96. 1
97. 1
98. 1
99. 1
100. 1
101. 1
102. 1
103. 1
104. 1
105. 1
106. 1
107. 1
108. 1
109. 1
110. 1
111. 1
112. 1
113. 1
114. 1
115. 2
116. 2
117. 1
118. 1
119. 1
120. 1
121. 1
122. 1
123. 2
124. 1
125. 1
126. 1
127. 1
128. 1
129. 1
130. 1
131. 1
132. 1
133. 1
134. 1
135. 1
136. 1
137. 1
138. 1
139. 1
140. 2
141. 1
142. 1
143. 1
144. 1
145. 1
146. 1
147. 1
148. 1
149. 1
150. 1
151. 1
152. 1
153. 1
154. 1
155. 2
156. 2
157. 1
158. 1
159. 2
160. 1
161. 1
162. 1
163. 2
164. 2
69. Rule Weigth 0.9
70. 0.9
71. 0.9
72. 0.9
73. 0.9
74. 0.9
75. 0.9
76. 0.9
77. 0.9
78. 0.9
79. 0.9
80. 0.9
81. 0.9
82. 0.9
83. 0.9
84. 0.9
85. 0.9
86. 0.9
87. 1
88. 0.9
89. 0.9
90. 0.9
91. 1
92. 0.9
93. 0.9
94. 0.9
95. 0.6
96. 0.9
97. 0.9
98. 0.9
99. 0.6
100. 0.9
101. 0.9
102. 0.9
103. 1
104. 1
105. 0.9
106. 0.9
107. 1
108. 1
109. 0.7
110. 1
111. 1
112. 1
113. 0.7
114. 1
115. 1
116. 1
117. 0.9
118. 0.9
119. 0.6
120. 0.9
121. 0.9
122. 0.9
123. 0.2
124. 0.9
125. 1
126. 1
127. 0.5
128. 1
129. 1
130. 1
131. 0.5
132. 1
133. 0.7
134. 1
135. 1
136. 1
137. 0.7
138. 1
139. 1
140. 1
141. 0.9
142. 0.9
143. 1
144. 0.9
145. 0.9
146. 0.9
147. 1
148. 0.9
149. 0.9
150. 1
151. 1
152. 1
153. 0.9
154. 1
155. 1
156. 1
157. 0.9
158. 1
159. 1
160. 1
161. 0.9
162. 1
163. 1
164. 1
69. Rule Connection 1
70. 1
71. 1
72. 1
73. 1
74. 1
75. 1
76. 1
77. 1
|
|
|
78. 1
79. 1
80. 1
81. 1
82. 1
83. 1
84. 1
85. 1
86. 1
87. 1
88. 1
89. 1
90. 1
91. 1
92. 1
93. 1
94. 1
95. 1
96. 1
97. 1
98. 1
99. 1
100. 1
101. 1
102. 1
103. 1
104. 1
105. 1
106. 1
107. 1
108. 1
109. 1
110. 1
111. 1
112. 1
113. 1
114. 1
115. 1
116. 1
117. 1
118. 1
119. 1
120. 1
121. 1
122. 1
123. 1
124. 1
125. 1
126. 1
127. 1
128. 1
129. 1
130. 1
131. 1
132. 1
133. 1
134. 1
135. 1
136. 1
137. 1
138. 1
139. 1
140. 1
141. 1
142. 1
143. 1
144. 1
145. 1
146. 1
147. 1
148. 1
149. 1
150. 1
151. 1
152. 1
153. 1
154. 1
155. 1
156. 1
157. 1
158. 1
159. 1
160. 1
161. 1
162. 1
163. 1
164. 1
>>
Представим ФП для каждой переменной в СНВ, созданной нами – рисунки 7.11 – 7.17


Рисунок 7.11 – Вид СНВ Рисунок 7.12 - Правила
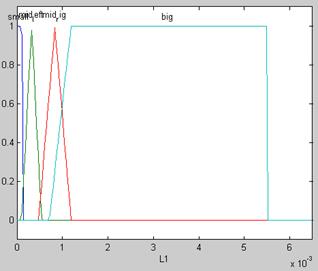

Рисунок 7.13 – ФП для L1 Рисунок 7.14 – ФП для L2


Рисунок 7.15 – ФП для t1 Рисунок 7.16 – ФП для t2

Рисунок 7.17 – ФП для location
Сравниваем результат работы программы обнаружения границ фаз с помощью четкой логики с результатом работы программы обнаружения границ фаз с помощью нечеткой логики.
Представим сначала в виде сравнения графиков на каждом участке
Четкая логика

Рисунок 7.1 – Участок кривой №11

Рисунок 7.2 – Участок кривой №12
Нечеткая логика

Рисунок 7.6 – Участок кривой №11

Рисунок 7.7 – Участок кривой №12

Рисунок 7.3 – Участок кривой №13

Рисунок 7.4 – Участок кривой №39

Рисунок 7.5 – Участок кривой №40

Рисунок 7.8 – Участок кривой №13
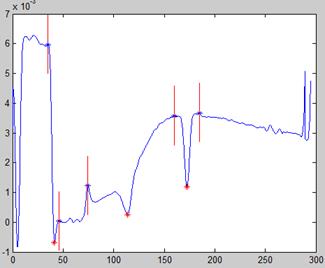
Рисунок 7.9 – Участок кривой №39

Рисунок 7.10 – Участок кривой №40
Сравним полученные результаты в четкой и нечеткой логике, выявим ошибки 1 и 2 рода:
При определении границ фаз возможны два вида ошибок: ошибки первого рода – фаза распознается как шум, и ошибки второго рода – шум распознается как фаза.
Анализируем участок №11 (рисунки 7.1 и 7.6)
3 фазы.
1 фаза распозналась.
2 фаза – при распознавании второй фазы в четкой логике появилась ошибка 1-го рода (фаза распозналась как шум).
3 фаза – распозналась в четкой логике, а в нечеткой шум распознался как фаза. Т.е. в нечеткой логике возникла ошибка 2-го рода (шум распознался как фаза)
Анализируем участок №12 (рисунки 7.2 и 7.7)
3 фазы.
Все 3 фазы распознались.
|
|
|
Анализируем участок №13 (рисунки 7.3 и 7.8)
3 фазы.
Все 3 фазы распознались в четкой логике + шум распознался как фаза(2-го рода).
Анализируем участок №39 (рисунки 7.4 и 7.9)
В нечеткой логике 3 фазы распознались правильно, а в четкой распознались шум как лишние 2 фазы. Следовательно в четкой логике возникли ошибка 2-го рода (шум распознался как фаза).
Анализируем участок №40 (рисунки 7.5 и 7.10)
3 фазы. В нечеткой логике – все правильно распознало, а в четкой – приняло фазу за шум. Поэтому в четкой логике возникла ошибка 1-го рода.
Изменяем веса правил № 26, 68, 79
Смотрим, как сказались изменения весов этих правил на результаты определения границ фаз. Результаты заносим в протокол.
26 – был вес 0.9, стал – 0.5.
68 - был вес 1, стал – 0.6.
79 - был вес 1, стал – 1.
|
|
|


