 |
Среднее квадратичное отклонение
|
|
|
|

Коэффициент вариации
 .
.
Расчетная таблица:
| ФИО | xi | xi-x | |xi-x| | (xi-x)2 | (xi-x)3 | (xi-x)4 |
| ААА | ||||||
| БББ | ||||||
| ВВВ | ||||||
| ГГГ | ||||||
| Итого |

2) показатели вариации
Размах вариации

Среднее линейное отклонение
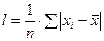
Дисперсия

Среднее квадратичное отклонение

Коэффициент вариации

Коэффициент асимметрии
Эксцесс
3) показатели структуры
Мода:
Медиана:
Дискретный вариационный ряд и его выборочные числовые характеристики:
Статистическая таблица, имеющая вид:
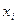 (значения признака) (значения признака)
|  (частоты) (частоты)
| ||

| 
| ||
| 
| ||
| … | … | ||
| … | …. | ||
| Итого: |  – объем выборки – объем выборки
|
Графическое изображение дискретного вариационного ряда – полигон.
Пример: Имеются данные о результатах экзаменов студенческой группы:
Балл 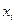
| Число студентов, 
| ||

1) показатели центра распределения (среднее значение)

2) показатели вариации
Размах вариации

Среднее линейное отклонение

Дисперсия

Среднее квадратичное отклонение

Коэффициент вариации
 .
.
Расчетная таблица:
| xi | ni | xini | |xi-x|´ni | (xi-x)2´ni | (xi-x)3´ni | (xi-x)4´ni | Si |
| Итого |
|
|
|
показатели центра распределения (среднее значение)

2) показатели вариации
Размах вариации
 =
=
Среднее линейное отклонение

Дисперсия
 =
=
Среднее квадратичное отклонение

Коэффициент вариации
 .
.
Коэффициент асимметрии
Эксцесс
Вывод:
3) показатели структуры
Мода:
Медиана. (для ее нахождения определяются накопленные частоты  ). Медиана равна значению признака, с накопленной частотой, большей
). Медиана равна значению признака, с накопленной частотой, большей  , при условии, что накопленная частота предыдущего значения признака меньше
, при условии, что накопленная частота предыдущего значения признака меньше  .
.
Непрерывный вариационный ряд и его выборочные числовые характеристики:
Статистическая таблица, имеющая вид:
 (значения признака) (значения признака)
|  (частоты) (частоты)
| ||
 – – 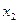
| 
| ||
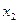 – – 
| 
| ||
| … | … | ||
| … | …. | ||
| Итого: |  – объем выборки – объем выборки
|
Графическим изображением ряда является гистограмма
Пример: Имеются данные о товарообороте магазинов:
| Товарооборот, млн. руб. | Число магазинов |
| 40—50 | |
| 50—60 | |
| 60—70 | |
| 70—80 | |
| 80—90 |
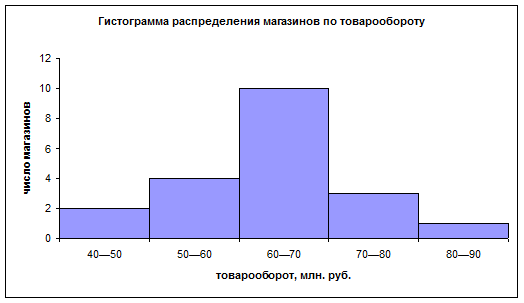
Для расчета среднего и показателей вариации нужно перейти к серединами интервалов.
| Товарооборот, млн. руб. | xi | ni | xini | |xi-x|´ni | (xi-x)2´ni | (xi-x)3´ni | (xi-x)4´ni | Si |
| 40—50 | ||||||||
| 50—60 | ||||||||
| 60—70 | ||||||||
| 70—80 | ||||||||
| 80—90 | ||||||||
| Итого | ||||||||
| Среднее | 63,5 | |||||||
| l | 35,5 | |||||||
| s | 9,63 | |||||||
| d | 15,17% | |||||||
| A | -0,0327 | |||||||
| E | 0,03018 |
Мода – это значение чаще всего встречающегося значения признака (товарооборота), которое вычисляется по формуле:
|
|
|

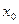 – левый конец модального интервала;
– левый конец модального интервала;
 – частота модального интервала;
– частота модального интервала;
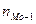 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным;
– частота интервала, следующего за модальным;
 – длина модального интервала.
– длина модального интервала.

Медиана – это значение признака, делящего выборку на две равные части, которое вычисляется по формуле:

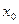 – левый конец медианного интервала;
– левый конец медианного интервала;
 – частота медианного интервала;
– частота медианного интервала;
 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
 – длина медианного интервала.
– длина медианного интервала.
Для нахождения медианы определим медианный интервал. Это интервал с накопленной частотой, большей  , при условии, что накопленная частота предыдущего интервала меньше
, при условии, что накопленная частота предыдущего интервала меньше  .
.

|
|
|


