 |
Задания для подготовки к экзамену
|
|
|
|
ПЕРЕЧЕНЬ ВОПРОСОВ И ПРАКТИЧЕСКИХ ЗАДАНИЙ
ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»
ДЛЯ СПЕЦИАЛЬНОСТИ 221413 «ТЕХНИЧЕСКОЕ РЕГУЛИРОВАНИЕ И УПРАВЛЕНИЕ КАЧЕСТВОМ»
Раздел 1. Развитие понятия о числе
1. Какие числа называются действительными?
2. Какие числа называют приближенными?
3. Что называют абсолютной погрешностью приближения? Что называют относительной погрешностью приближения? Какая погрешность характеризует качество приближения?
4. Опишите правило округления приближенных чисел.
Раздел 2. Решение треугольников в профессиональных задачах
5. Дайте определение тригонометрических функций числового аргумента.
6. В чём заключается свойство периодичности тригонометрических функций?
7. Какие тригонометрические функции являются чётными, какие нечётными?
8. Каковы знаки тригонометрических функций в различных четвертях?
9. Перечислите основные тригонометрические тождества.
10. Каков алгоритм использования формул приведения?
Раздел 3. Измерения в геометрии
11. Сформулируйте определение вектора. Что называют координатами вектора на плоскости? Как вычисляется скалярное произведение векторов в координатах?
12. Проанализируйте, как, зная координаты векторов на плоскости, найти их длины и угол между ними.
13. Запишите формулу, позволяющую вычислить расстояние между двумя точками плоскости, заданными своими координатами.
14. Как применяется координатный метод в решении профессиональных задач?
Раздел 4. Основы дискретной математики
15. Раскройте понятие множества. Какие существуют способы задания множеств? Перечислите виды множеств и приведите примеры.
16. Операции над множествами: объединение, пересечение, разность, симметрическая разность. Сформулируйте определения, проиллюстрируйте с помощью диаграмм Эйлера-Венна и перечислите свойства данных операций.
|
|
|
17. Сформулируйте определения универсального множества и дополнения к множеству, проиллюстрируйте диаграммами Эйлера-Венна. Приведите примеры.
18. Раскройте понятие подмножества. Приведите примеры множества и его подмножеств. Сформулируйте определение булеана множества. Запишите формулу, позволяющую вычислить мощность булеана конечного множества.
19. Высказывания: определение, виды, способы составления и примеры.
20. Перечислите основные логические операции над высказываниями, сформулируйте их определения и приведите примеры.
21. Сформулируйте определение формулы алгебры логики. Какая формула называется тождественно истинной, тождественно ложной, выполнимой? Приведите примеры.
22. Таблица истинности формулы алгебры логики: основные понятия, техника построения и практическое применение.
Раздел 5. Основы теории вероятностей и математической статистики
23. Сформулируйте определение перестановки. Приведите примеры. Как осуществляется подсчет числа перестановок?
24. Сформулируйте определение размещения. Приведите примеры. Как осуществляется подсчет числа размещений?
25. Сформулируйте определение сочетания. Приведите примеры. Как осуществляется подсчет числа сочетаний?
26. Сформулируйте классическое определение вероятности. Приведите примеры задач на вычисление вероятностей в простейших случаях.
27. Дайте определение случайной величины. Какая случайная величина называется дискретной, непрерывной? Приведите примеры дискретных и непрерывных случайных величин.
28. Какие числовые характеристики случайной величины существуют? Приведите формулы для их расчета.
29. Проанализируйте, чем выборка отличается от генеральной совокупности. Как осуществляется первичная обработка статистических данных.
|
|
|
ЗАДАНИЯ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ
1.1.Найдите абсолютную и относительную погрешности приближенного значения а величины х:
1) 
; 2) 
.
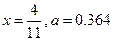1.2. Округлите с недостатком, с избытком и по правилам до сотых десятичные дроби: 1) 0,3857; 2) 1.2345;
3) 24.0087. Найдите абсолютную погрешность вычислений.
1.3. Запишите в стандартном виде: 0,723; 0.045; 507.25; 
2.
2.1.а) Найдите 12% от 400, б) Найдите число, если 21% его равны 0,651.
2.2. Решите задачи:
а) Объем бочки 540л. Водой заполнили 85% этой бочки. Сколько литров воды в бочке?
б) За контрольную работу было поставлено 15% пятерок. Сколько учеников писало контрольную работу, если пятерки получили 6 учеников.
в) Смешали 4кг сушеных яблок и 6кг сушеных груш. Сколько процентов полученной смеси составляют яблоки?
г) В первый день вспахали 30% поля, а во второй 40% остатка. После этого осталось вспахать 252га. Какова площадь поля?
3. Упростите выражения:
3.1. 
3.2. 
3.3. 
3.4. 
3.5. 
3.6.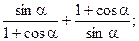 
3.7. 
.
4.
4.1. Найдите координаты векторов 
и 
и вычислите угол между ними:
а) 
, 
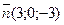; б) 
, 
.
4.2.Найдите координаты вектора 
и вычислите его длину, если 
, 
, 
.
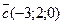4.3.Найдите скалярное произведение векторов: а)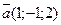 
, 
; б) ,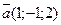 
.
4.5.При каком значении n векторы перпендикулярны: а)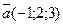 
, 
; б) 
, 
.
4.6.Найдите значение m, если векторы взаимно перпендикулярны: 
, 
.
4.7.Найдите значение y и z, если векторы 
и 
коллинеарны.
4.8.Найдите координаты конца В вектора 
(1;-4;8), если координаты начала - точки А (1;0;2).
4.9. Даны точки А (1;3;0) и В (2;3;-1), а также вектор 
. Найдите координаты векторов 
и 
и ответьте на вопрос, коллинеарны ли эти векторы.
5.
5.1. Даны множества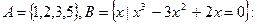 
Найдите следующие множества: 
;
5.2 Запишите все подмножества множества А. Найдите мощность булеана данного множества.
6. Изобразите множество с помощью диаграмм Эйлера-Венна:
6.1 
18.2 
18.3 
7. Выясните с помощью диаграмм Эйлера-Венна, является ли теоретико-множественное соотношение тождеством:
7.1 
7.2 
7.3 
7.4 
7.5 
8. Решите задачу: каждый студент группы АС 1-21 в свободное время занимается дискретной математикой или теорией вероятностей. Сколько студентов в группе, если 23 увлекаются дискретной математикой, 12- теорией вероятностей, а – 7 совмещают обе дисциплины?
9. Выясните, какие из следующих предложений являются высказываниями:
|
|
|
9.1 В романе А.С. Пушкина «Евгений Онегин» 136245 букв.
9.2 Студент строительного отделения ЯГК.
9.3 Дискретная математика – самая увлекательная дисциплина.
10. Составьте таблицу истинности для формулы алгебры высказываний:
10.1 
; 10.2 
; 10.3 
.
11. Выясните с помощью таблицы истинности, будет ли формула логики выполнимой, тождественно - истинной или тождественно - ложной:
11.1 
; 11.2 
; 11.3 
.
12. Проверьте равносильность формул с помощью таблицы истинности:
12.1 
; 12.2 
;
12.3 
.
13. Постройте таблицу значений для булевой функции:
13.1 
;13.2 
; 41.3 
.
14. Вычислите:
14.1.  ;
| 14.2.  ;
| 14.3.  .
|
15. Решите задачу:
15.1. Сколько различных двузначных чисел можно образовать из цифр 2, 3, 5, 7 при условии, что в числе нет одинаковых цифр?
15.2. В комиссию по дисциплине «Электротехника и электроника» входят 3 преподавателя колледжа. Сколькими способами можно составить комиссию, если в колледже 7 преподавателей этой дисциплины?
15.3. К банкомату за получением стипендии одновременно подошли 5 студентов. Сколькими способами они могут выстроиться в очередь?
16. Решите задачу:
16.1. В урне 10 стандартных и 3 бракованных детали. Из урны случайным образом берут одну деталь. Какова вероятность того, что деталь окажется стандартной?
16.2. В группе из 30 человек 22 юноши, остальные – девушки. Для опроса преподаватель вызывает одного студента. Какова вероятность того, что опрошенной окажется девушка?
17. Дискретная случайная величина X задана законом распределения. Найдите недостающую вероятность и числовые характеристики дискретной случайной величины X:
17.1.
| 17.2.
|
18. С целью изучения динамики спроса на компьютеры фирма ежедневно подсчитала число проданных компьютеров в течение месяца: 3, 5, 4, 7, 0, 1, 3, 5, 5, 2, 3, 4, 3, 6, 6, 2, 0, 5, 3, 5, 6, 4, 4, 3, 1, 4, 2, 2, 4, 5. Составьте статистическое распределение выборки, постройте полигон частот, найдите числовые характеристики выборки.
|
|
|
