Контроль погрешности измерений

 

I Оценка характеристик погрешности измерения с применением стандартных образцов

 

Таблица 1 - Исходные данные единичного анализа образцов для оценивания

№ результата измерений	С1=0,5; ∆=0,01		С1=2,5; ∆=0,05		С1=5,0; ∆=0,1
	Опыт 1	Опыт 2	Опыт 1	Опыт 2	Опыт 1	Опыт 2
1	0,475	0,486	2,5	2,509	5,19	5,14
2	0,476	0,489	2,49	2,5	5,18	5,12
3	0,478	0,49	2,489	2,51	5,17	5,11
4	0,479	0,491	2,488	2,511	5,18	5,13
5	0,48	0,492	2,487	2,512	5,16	5,11
6	0,481	0,493	2,486	2,513	5,15	5,16
7	0,482	0,494	2,485	2,514	5,14	5,13
8	0,483	0,495	2,484	2,516	5,13	5,0
9	0,484	0,496	2,483	2,517	5,12	4,99
10	0,485	0,497	2,482	2,518	5,11	5,11

 

. Расчет погрешности для С₁=0,5

Рассчитаем среднее арифметическое значение результатов анализа, полученных в условиях повторяемости по формуле:

 

 

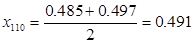
Для полученных результатов определим дисперсию по формуле:

 

 

Определяем среднее квадратичное отклонение результатов анализа, полученных в условиях повторяемости по формуле:

 

 

при этом

 

Находим значение:

 

 

Тогда средне-квадратичное отклонение, полученное в условиях повторяемости и воспроизводимости будет определяться по формуле:

 

 

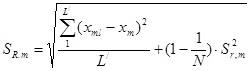
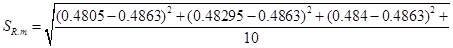
Определим математическое ожидание, используя формулу:

 

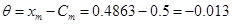
Таким образом, рассчитаем критерий Стъюдента:

 

 

Табличное значение критерия Стъюдента для числа степеней свободы f=10-1=9 составляет t_т= 2,2622. Поскольку t_p< t_т, то математическое ожидание является незначимым и в формуле определения погрешности не учитывается, тогда:

 

 (где z=1.96 при р=0,95)

 

2. Расчет погрешности для С₂=2,5 (аналогично предыдущему расчету)

Рассчитаем среднее арифметическое значение результатов анализа, полученных в условиях повторяемости по формуле:

 

 

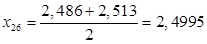
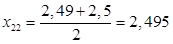
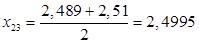
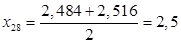
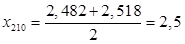
Для полученных результатов определим дисперсию по формуле:

 

 

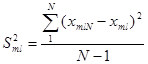
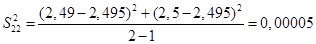
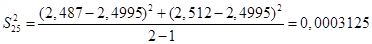
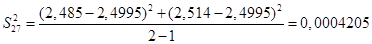
Определяем среднее квадратичное отклонение результатов анализа, полученных в условиях повторяемости по формуле:

 

 

 

при этом

 

Находим значение:

 

 

Тогда среднеквадратичное отклонение, полученное в условиях повторяемости и воспроизводимости будет определяться по формуле:

 

 

Определим математическое ожидание, используя формулу:

 

 

Таким образом, рассчитаем критерий Стъюдента:

 

 

Табличное значение критерия Стъюдента для числа степеней свободы f=10-1=9 составляет t_т= 2,2622. Поскольку t_p< t_т, то математическое ожидание является незначимым и в формуле определения погрешности не учитывается, тогда:  (где z=1.96 при р=0,95)

. Расчет погрешности для С₃=5,0 (аналогично предыдущим расчетам)

Рассчитаем среднее арифметическое значение результатов анализа, полученных в условиях повторяемости по формуле:

 

 

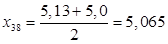
Для полученных результатов определим дисперсию по формуле:

 

 

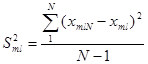
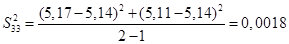
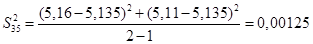
Определяем среднее квадратичное отклонение результатов анализа, полученных в условиях повторяемости по формуле:

 

 

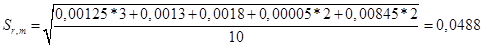
при этом

Находим значение:

 

 

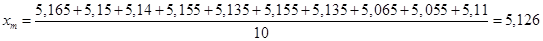
Тогда среднеквадратичное отклонение, полученное в условиях повторяемости и воспроизводимости будет определяться по формуле:

 

 

Определим математическое ожидание, используя формулу:

 

 

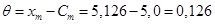
Таким образом, рассчитаем критерий Стъюдента:

 

 

 

Табличное значение критерия Стъюдента для числа степеней свободы f=10-1=9 составляет t_т= 2,2622. Поскольку t_p< t_т, то математическое ожидание является незначимым и в формуле определения погрешности не учитывается, тогда:

 

 (где z=1.96 при р=0,95)

 

II Оценивание систематической составляющей погрешности методом добавок

 

Таблица 2 - Экспериментальные данные результатов измерений для оценки систематической составляющей погрешности с использованием метода добавок

№ результата измерений	Значение результатов измерений в пробе без добавки, Xl	Значение результатов измерений в пробе с добавкой, Xl/	Значение результатов экспериментально найденной добавки, Xlд
1	0,585	1,021	0,436
2	0,623	1,150	0,527
3	0,487	0,988	0,501
4	0,520	1,123	0,603
5	0,688	1,205	0,517
6	0,563	1,006	0,443
7	0,412	0,986	0,574
8	0,574	1,135	0,561
9	0,444	1,002	0,558
10	0,562	1,089	0,527

 

Определим среднее арифметическое в каждом случае по следующим формулам:

 

 

; ;

 

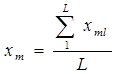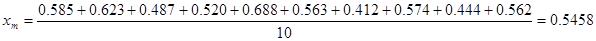
Определяем среднеквадратичное отклонение для:

пробы без добавки

 

 

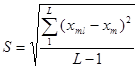
пробы с добавкой

 

Оцениваем математическое ожидание:

 

 

Определяем критерий Стъюдента:

 

 

Табличное значение критерия Стъюдента для числа степеней свободы f=10-1=9 составляет t_т= 2,2622. Поскольку t_p< t_т, то математическое ожидание является незначимым и в формуле определения погрешности не учитывается, тогда:

 

 (где z=1.96 при р=0,95)

 

III Оценивание погрешности с применением метода добавок в сочетании с разбавлением

 

Таблица 3 - Экспериментальные данные результатов измерений для оценки систематической составляющей погрешности с использованием метода добавок в сочетании с разбавлением

№ результата измерений	Значение результатов измерений в пробе без добавки, Xl	Значение результатов измерений в разбавленной пробе, Yl	Значение результатов измерений в разбавленной, Zl
1	0,551	0,250	0,532
2	0,496	0,221	0,486
3	0,548	0,253	0,529
4	0,490	0,226	0,455
5	0,579	0,263	0,558
6	0,497	0,212	0,491
7	0,557	0,261	0,544
8	0,587	0,275	0,577
9	0,478	0,237	0,463
10	0,596	0,286	0,559

 

Определим математическое ожидание процесса разбавления:

 

 

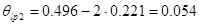
Найдем математическое ожидание погрешности, связанное с добавкой:

 

 

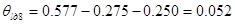
Определяем среднее арифметическое в обоих случаях:

 

;

 

Находим среднеквадратичное отклонение:

 

;

 

Определяем критерий Стъюдента для:

 

разбавленных проб

 

 

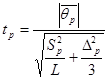
проб с добавкой

 

 

Поскольку табличное значение критерия Стьюдента составляет t_т = 2,2622, при этом t_p < t_т и t_д < t_т, то математические ожидания являются незначительными и при расчете погрешности не учитываются.

 

 

Общая погрешность:

 

 

Найдем :

Определяем среднее арифметическое значение проб без добавки:

 

 

Определяем среднеквадратичное отклонение:

 

 

Таким образом, общая погрешность составит:

 

 

Заключение

 

Был проведен контроль точности результатов конечного химического анализа по оперативному контролю повторяемости и воспроизводимости, с применением метода добавок и разбавления и метод добавок в сочетании с разбавлением. На основании проделанного расчета можно сделать вывод, что результаты всех проведенных анализов соответствуют требованиям.

 

Список использованной литературы

 

1 Сметанин В.И. Защита окружающей среды от отходов производства и потребления.- М.: Колос, 2000.-232 с.

http://www.ekowater.ru

МИ 2336-2002 Рекомендации по метрологии. Показатели точности правильности и прецизионности методик количественного анализа, методы оценки.

ГОСТ РИСО 5725 - 1 - 2022 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: