 |
Перечень условных обозначений
|
|
|
|
Содержание
Перечень условных обозначений
Введение
1 Определение и основные свойства конечных групп с условием плотности для 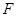 -субнормальных подгрупп
-субнормальных подгрупп
2 Свойства максимальных подгрупп в группах с плотной системой 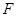 -субнормальных подгрупп
-субнормальных подгрупп
3 Описание конечных не 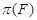 -групп с плотной системой
-групп с плотной системой 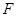 -субнормальных подгрупп
-субнормальных подгрупп
Заключение
Литература
Перечень условных обозначений
В работе все рассматриваемые группы предполагаются конечными. Используются обозначения, принятые в книгах. Буквами  обозначаются простые числа.
обозначаются простые числа.
Будем различать знак включения множеств  и знак строгого включения
и знак строгого включения  ;
;
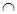 и
и 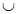 --- соответственно знаки пересечения и объединения множеств;
--- соответственно знаки пересечения и объединения множеств;
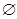 --- пустое множество;
--- пустое множество;
 --- множество всех
--- множество всех 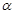 , для которых выполняется условие
, для которых выполняется условие  ;
;
 --- множество всех простых чисел;
--- множество всех простых чисел;
 --- некоторое множество простых чисел, т.е.
--- некоторое множество простых чисел, т.е.  ;
;
 --- дополнение к
--- дополнение к  во множестве всех простых чисел; в частности,
во множестве всех простых чисел; в частности,  ;
;
примарное число --- любое число вида  ;
;
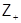 --- множество всех целых положительных чисел.
--- множество всех целых положительных чисел.
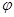 --- некоторое линейное упорядочение множества всех простых чисел
--- некоторое линейное упорядочение множества всех простых чисел  .
.
Запись  означает, что
означает, что  предшествует
предшествует  в упорядочении
в упорядочении 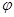 ,
,  .
.
Пусть  --- группа. Тогда:
--- группа. Тогда:
 --- порядок группы
--- порядок группы  ;
;
 --- порядок элемента
--- порядок элемента  группы
группы  ;
;
 --- единичный элемент и единичная подгруппа группы
--- единичный элемент и единичная подгруппа группы  ;
;
 --- множество всех простых делителей порядка группы
--- множество всех простых делителей порядка группы  ;
;
 --- множество всех различных простых делителей натурального числа
--- множество всех различных простых делителей натурального числа 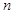 ;
;
 --группа --- группа
--группа --- группа  , для которой
, для которой  ;
;
 --группа --- группа
--группа --- группа  , для которой
, для которой 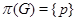 ;
;
 --- подгруппа Фраттини группы
--- подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп группы
, т.е. пересечение всех максимальных подгрупп группы  ;
;
 --- подгруппа Фиттинга группы
--- подгруппа Фиттинга группы  , т.е. произведение всех нормальных нильпотентных подгрупп группы
, т.е. произведение всех нормальных нильпотентных подгрупп группы  ;
;
 --- коммутант группы
--- коммутант группы  ;
;
|
|
|
 ---
---  --холловская подгруппа группы
--холловская подгруппа группы  ;
;
 --- силовская
--- силовская  --подгруппа группы
--подгруппа группы  ;
;
 --- дополнение к силовской
--- дополнение к силовской  --подгруппе в группе
--подгруппе в группе  , т.е.
, т.е. 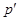 --холловская подгруппа группы
--холловская подгруппа группы  ;
;
 --- группа всех автоморфизмов группы
--- группа всех автоморфизмов группы  ;
;
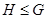 ---
---  является подгруппой группы
является подгруппой группы  ;
;
нетривиальная подгруппа --- неединичная собственная подгруппа;
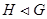 ---
---  является нормальной подгруппой группы
является нормальной подгруппой группы  ;
;
 --- подгруппа
--- подгруппа  характеристична в группе
характеристична в группе  , т.е.
, т.е. 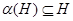 для любого автоморфизма
для любого автоморфизма  ;
;
 --- индекс подгруппы
--- индекс подгруппы  в группе
в группе  ;
;
 ;
;
 --- централизатор подгруппы
--- централизатор подгруппы  в группе
в группе  ;
;
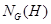 --- нормализатор подгруппы
--- нормализатор подгруппы  в группе
в группе  ;
;
 --- центр группы
--- центр группы  ;
;
 --- циклическая группа порядка
--- циклическая группа порядка 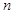 ;
;
Если  и
и  --- подгруппы группы
--- подгруппы группы  , то:
, то:
 --- прямое произведение подгрупп
--- прямое произведение подгрупп  и
и  ;
;
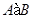 --- полупрямое произведение нормальной подгруппы
--- полупрямое произведение нормальной подгруппы  и подгруппы
и подгруппы  .
.
Группа  называется:
называется:
примарной, если  ;
;
бипримарной, если  .
.
Скобки  применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
 --- подгруппа, порожденная всеми
--- подгруппа, порожденная всеми 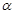 , для которых выполняется
, для которых выполняется  .
.
Группу  называют
называют  --нильпотентной, если
--нильпотентной, если 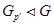 .
.
Группу  порядка
порядка 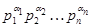 называют
называют 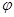 --дисперсивной, если выполняется
--дисперсивной, если выполняется  и для любого
и для любого 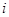
 имеет нормальную подгруппу порядка
имеет нормальную подгруппу порядка 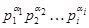 . Если при этом упорядочение
. Если при этом упорядочение 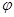 таково, что
таково, что  всегда влечет
всегда влечет  , то
, то 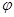 --дисперсивная группа называется дисперсивной по Оре.
--дисперсивная группа называется дисперсивной по Оре.
Цепь --- это совокупность вложенных друг в друга подгрупп. Ряд подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через единицу. Цепь  называется
называется 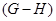 -цепью (с индексами
-цепью (с индексами  ); если при этом
); если при этом 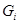 является максимальной подгруппой в
является максимальной подгруппой в  для любого
для любого  , то указанная цепь называется максимальной
, то указанная цепь называется максимальной 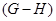 -цепью.
-цепью.
Ряд подгрупп  называется:
называется:
субнормальным, если  для любого
для любого  ;
;
нормальным, если  для любого
для любого 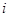 .
.
Нормальный ряд называется главным, если  является минимальной нормальной подгруппой в
является минимальной нормальной подгруппой в  для всех
для всех  .
.
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Так же обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
|
|
|
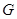 --- класс всех групп;
--- класс всех групп;
 --- класс всех абелевых групп;
--- класс всех абелевых групп;
 --- класс всех нильпотентных групп;
--- класс всех нильпотентных групп;
 --- класс всех разрешимых групп;
--- класс всех разрешимых групп;
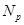 --- класс всех
--- класс всех  --групп;
--групп;
 --- класс всех сверхразрешимых групп.
--- класс всех сверхразрешимых групп.
Пусть  --- некоторый класс групп и
--- некоторый класс групп и 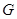 --- группа, тогда:
--- группа, тогда:
 ---
---  --корадикал группы
--корадикал группы 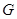 , т.е. пересечение всех тех нормальных подгрупп
, т.е. пересечение всех тех нормальных подгрупп  из
из 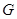 , для которых
, для которых  . Если
. Если  --- формация, то
--- формация, то  является наименьшей нормальной подгруппой группы
является наименьшей нормальной подгруппой группы 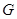 , факторгруппа по которой принадлежит
, факторгруппа по которой принадлежит  . Если
. Если  --- формация всех сверхразрешимых групп, то
--- формация всех сверхразрешимых групп, то 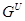 называется сверхразрешимым корадикалом группы
называется сверхразрешимым корадикалом группы 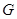 .
.
Формация  называется насыщенной, если всегда из
называется насыщенной, если всегда из 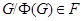 следует, что и
следует, что и  . Класс групп
. Класс групп  называется наследственным или
называется наследственным или  -замкнутым, если из того, что
-замкнутым, если из того, что 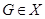 , следует, что и каждая подгруппа группы
, следует, что и каждая подгруппа группы 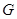 также принадлежит
также принадлежит  .
.
Пусть  --- некоторая непустая формация. Максимальная подгруппа
--- некоторая непустая формация. Максимальная подгруппа 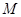 группы
группы 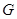 называется:
называется:
 -нормальной, если
-нормальной, если  ;
;
 -абнормальной, если
-абнормальной, если  .
.
Максимальная 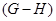 -цепь
-цепь  называется
называется  -субнормальной, если для любого
-субнормальной, если для любого  подгруппа
подгруппа 
 -нормальна в
-нормальна в  . Подгруппа
. Подгруппа  группы
группы 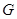 называется
называется  -субнормальной, если существует хотя бы одна
-субнормальной, если существует хотя бы одна  -субнормальная максимальная
-субнормальная максимальная 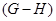 -цепь.
-цепь.
Группа 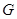 называется группой с плотной системой
называется группой с плотной системой  -субнормальных подгрупп, если для любых двух различных подгрупп
-субнормальных подгрупп, если для любых двух различных подгрупп  и
и  группы
группы  , из которых первая содержится во второй и не максимальна в ней, в группе
, из которых первая содержится во второй и не максимальна в ней, в группе  существует такая
существует такая  -субнормальная подгруппа
-субнормальная подгруппа  , что
, что  . В этом случае также говорят, что множество
. В этом случае также говорят, что множество  -субнормальных в
-субнормальных в 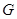 подгрупп плотно.
подгрупп плотно.
Введение
Изучение строения групп по заданным свойствам системы их подгрупп является одним из основных направлений в теории конечных групп. Отметим, что темп и глубина таких исследований непрерывно возрастают. Это направление изучения групп берет свое начало с групп Миллера-Морено, групп Шмидта. В качестве свойств, налагаемых на системы подгрупп, рассматривались абелевость, нормальность, субнормальность, дополняемость и др. Это направление получило широкое развитие в работах многих ведущих алгебраистов.
С дедекиндовых групп, то есть групп, у которых нормальны все подгруппы, началось изучение различных (как конечных, так и бесконечных) групп, у которых некоторая система подгрупп  удовлетворяет условию нормальности. Описание конечных дедекиндовых групп дано в работе Р. Дедекинда, а бесконечных в работе Р. Бэра. Эти работы определили важное направление исследований в теории групп. Главной целью этого направления является описание обобщенно дедекиндовых групп. Эти обобщения дедекиндовых групп осуществляются либо путем сужения системы подгрупп
удовлетворяет условию нормальности. Описание конечных дедекиндовых групп дано в работе Р. Дедекинда, а бесконечных в работе Р. Бэра. Эти работы определили важное направление исследований в теории групп. Главной целью этого направления является описание обобщенно дедекиндовых групп. Эти обобщения дедекиндовых групп осуществляются либо путем сужения системы подгрупп  , то есть подгрупп нормальных во всей группе, либо ослабления свойства нормальности для подгрупп из
, то есть подгрупп нормальных во всей группе, либо ослабления свойства нормальности для подгрупп из  . Среди таких обобщений выделим следующие исследования.
. Среди таких обобщений выделим следующие исследования.
|
|
|
Первое существенное обобщение дедекиндовых групп принадлежит О.Ю. Шмидту. Он описал конечные группы с одним и двумя классами сопряженных ненормальных подгрупп, а также установил нильпотентность конечной группы, у которой нормальны все максимальные подгруппы. Конечные группы с нормальными 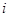 -тыми максимальными подгруппами изучали Б. Хупперт и З. Янко. Д.Бакли изучал конечные группы, у которых нормальны все минимальные подгруппы.
-тыми максимальными подгруппами изучали Б. Хупперт и З. Янко. Д.Бакли изучал конечные группы, у которых нормальны все минимальные подгруппы.
Значительные расширения класса дедекиндовых групп возникают при переходе от условия нормальности к различным ее обобщениям, как, например, к квазинормальности, субнормальности, нормализаторным условиям и др.
В начале 70-х годов по инициативе С.Н.Черникова началось изучение групп с плотными системами подгрупп. Система подгрупп группы  , обладающая некоторым свойством
, обладающая некоторым свойством  , называется плотной в
, называется плотной в  , если для любых двух подгрупп
, если для любых двух подгрупп  из
из  , где
, где  не максимальна в
не максимальна в  , найдется
, найдется  -подгруппа
-подгруппа  такая, что
такая, что  . Группы с плотной системой дополняемых подгрупп были изучены С.Н.Черниковым.
. Группы с плотной системой дополняемых подгрупп были изучены С.Н.Черниковым.
В 1974 году С.Н.Черников поставил следующий вопрос: каково строение группы  , в которой множество всех ее субнормальных подгрупп плотно? Ответ на этот вопрос был получен А.Манном и В.В.Пылаевым.
, в которой множество всех ее субнормальных подгрупп плотно? Ответ на этот вопрос был получен А.Манном и В.В.Пылаевым.
Заметим, что в теории формаций понятие субнормальности обобщается следующим образом. Говорят, что подгруппа  является
является  -субнормальной в
-субнормальной в  , если существует цепь подгрупп
, если существует цепь подгрупп
|
|
|

такая, что  является
является  -нормальной максимальной подгруппой в
-нормальной максимальной подгруппой в  для любого
для любого  . Если
. Если  совпадает с классом всех нильпотентных групп (который является, конечно,
совпадает с классом всех нильпотентных групп (который является, конечно,  -замкнутой насыщенной формацией), то
-замкнутой насыщенной формацией), то  -субнормальная подгруппа оказывается субнормальной.
-субнормальная подгруппа оказывается субнормальной.
В связи с развитием теории формаций большое внимание стало уделяться исследованию конечных групп, насыщенных  --подгруппами,
--подгруппами,  --субнормальными или
--субнормальными или  --абнормальными подгруппами. В этом направлении проводили свои исследования Л.А.Шеметков, Гашюц, Картер, Шмид, Хоукс и другие.
--абнормальными подгруппами. В этом направлении проводили свои исследования Л.А.Шеметков, Гашюц, Картер, Шмид, Хоукс и другие.
Ясно, что вопрос С.Н.Черникова можно сформулировать в следующей общей форме: если  ---
---  -замкнутая насыщенная формация, то каково строение группы, в которой множество всех ее
-замкнутая насыщенная формация, то каково строение группы, в которой множество всех ее  -субнормальных подгрупп плотно?
-субнормальных подгрупп плотно?
В таком виде вопрос С.Н.Черникова был исследован в работе для случая, когда  --- класс всех
--- класс всех  -нильпотентных групп. В настоящей работе мы исследуем данный вопрос в случаях, когда
-нильпотентных групп. В настоящей работе мы исследуем данный вопрос в случаях, когда  --- произвольная
--- произвольная  -замкнутая насыщенная формация либо
-замкнутая насыщенная формация либо  -нильпотентных, либо
-нильпотентных, либо  -дисперсивных, либо сверхразрешимых групп.
-дисперсивных, либо сверхразрешимых групп.
1. Определение и основные свойства конечных групп с условием плотности для  -субнормальных подгрупп
-субнормальных подгрупп
Опишем вначале общие свойства конечных групп с плотной системой  -субнормальных подгрупп, где
-субнормальных подгрупп, где  --- произвольная насыщенная
--- произвольная насыщенная 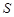 -замкнутая формация.
-замкнутая формация.
Группа 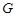 называется группой с плотной системой
называется группой с плотной системой  -субнормальных подгрупп, если для любых двух различных подгрупп
-субнормальных подгрупп, если для любых двух различных подгрупп  и
и  группы
группы  , из которых первая содержится во второй и не максимальна в ней, в группе
, из которых первая содержится во второй и не максимальна в ней, в группе  существует такая
существует такая  -субнормальная подгруппа
-субнормальная подгруппа  , что
, что  . В этом случае также говорят, что множество
. В этом случае также говорят, что множество  -субнормальных в
-субнормальных в 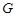 подгрупп плотно.
подгрупп плотно.
Пусть  --- непустая
--- непустая 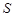 -замкнутая насыщенная формация,
-замкнутая насыщенная формация,  --- подгруппа группы
--- подгруппа группы 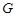 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:
1) 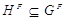 ;
;
2) если 
 -субнормальна в
-субнормальна в 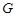 и
и  является подформацией формации
является подформацией формации  , то
, то 
 -субнормальна в
-субнормальна в 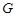 .
.
Доказательство. 1) Из того, что

следует, что  . Это значит, что
. Это значит, что  .
.
2) Так как 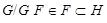 , то
, то 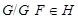 и
и 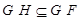 . Отсюда следует, что каждая
. Отсюда следует, что каждая  -нормальная максимальная подгруппа является
-нормальная максимальная подгруппа является  -нормальной максимальной. Лемма доказана.
-нормальной максимальной. Лемма доказана.
Пусть  --- непустая
--- непустая  -замкнутая насыщенная формация. Если множество всех
-замкнутая насыщенная формация. Если множество всех  -субнормальных подгрупп плотно в группе
-субнормальных подгрупп плотно в группе  , то справедливы следующие утверждения:
, то справедливы следующие утверждения:
1) если 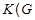 , то в
, то в  множество всех
множество всех  -субнормальных подгрупп плотно;
-субнормальных подгрупп плотно;
2) если  --- подгруппа из
--- подгруппа из  , то множество всех
, то множество всех  -субнормальных подгрупп из
-субнормальных подгрупп из  является плотным в
является плотным в  .
.
Доказательство. 1) Пусть  --- нормальная подгруппа группы
--- нормальная подгруппа группы  . В фактор-группе
. В фактор-группе  рассмотрим две произвольные подгруппы
рассмотрим две произвольные подгруппы 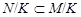 , из которых первая не максимальна во второй. Тогда
, из которых первая не максимальна во второй. Тогда  и
и  не максимальна в
не максимальна в  . По условию, в
. По условию, в  существует
существует  -субнормальная подгруппа
-субнормальная подгруппа  такая, что
такая, что  . Следовательно,
. Следовательно, 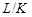
 -субнормальна в
-субнормальна в  .
.
|
|
|
2) Пусть  --- подгруппа из
--- подгруппа из  и
и  --- две произвольные подгруппы из
--- две произвольные подгруппы из  такие, что
такие, что  не максимальна в
не максимальна в  . Тогда, по условию, в
. Тогда, по условию, в  существует
существует  -субнормальная подгруппа
-субнормальная подгруппа  , для которой
, для которой  . Ввиду леммы,
. Ввиду леммы, 
 -субнормальна в
-субнормальна в  . Лемма доказана.
. Лемма доказана.
Если  ---
---  -субнормальная подгруппа группы
-субнормальная подгруппа группы  , то
, то
 .
.
Доказательство. По определению, существует цепь

такая, что  является
является  -нормальной максимальной подгруппой в
-нормальной максимальной подгруппой в  при любом
при любом  . Таким образом,
. Таким образом,  и потому
и потому

для каждого  . Следовательно,
. Следовательно,  .
.
Пусть  --- непустая
--- непустая 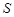 -замкнутая насыщенная формация,
-замкнутая насыщенная формация,  --- группа, у которой множество всех ее
--- группа, у которой множество всех ее  -субнормальных подгрупп плотно. Справедливы следующие утверждения:
-субнормальных подгрупп плотно. Справедливы следующие утверждения:
1) если  ---
---  -абнормальная максимальная подгруппа группы
-абнормальная максимальная подгруппа группы  , то либо
, то либо  , либо каждая
, либо каждая  -абнормальная максимальная подгруппа из
-абнормальная максимальная подгруппа из 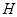 принадлежит
принадлежит  ;
;
2) если 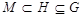 и
и  , то
, то  либо максимальна в
либо максимальна в 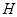 , либо
, либо  -субнормальна в
-субнормальна в  .
.
Доказательство. Докажем сначала 1). Пусть 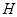 ---
---  -абнормальная максимальная подгруппа, не принадлежащая
-абнормальная максимальная подгруппа, не принадлежащая  . Допустим, что
. Допустим, что 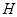 обладает
обладает  -абнормальной максимальной подгруппой
-абнормальной максимальной подгруппой 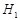 , не принадлежащей
, не принадлежащей  . Тогда в
. Тогда в  имеется
имеется  -абнормальная максимальная подгруппа
-абнормальная максимальная подгруппа  . По условию, в
. По условию, в  найдется такая
найдется такая  -субнормальная подгруппа
-субнормальная подгруппа  , что
, что  . Ясно, что
. Ясно, что  . По лемме,
. По лемме,
 .
.
Так как 
 -субнормальна, то она содержится в
-субнормальна, то она содержится в  -нормальной максимальной подгруппе, и поэтому
-нормальной максимальной подгруппе, и поэтому  . Значит,
. Значит, 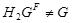 . Последнее противоречит следующему:
. Последнее противоречит следующему:
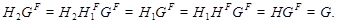
Докажем 2). Пусть 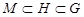 и
и  . Допустим, что
. Допустим, что  не максимальна в
не максимальна в 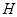 . По условию, в
. По условию, в  найдется такая
найдется такая  -субнормальная подгруппа
-субнормальная подгруппа  , что
, что  . Так как
. Так как 
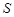 -замкнута, то
-замкнута, то  . Поэтому
. Поэтому 
 -субнормальна в
-субнормальна в  . Теперь ясно, что
. Теперь ясно, что 
 -субнормальна в
-субнормальна в  . Лемма доказана.
. Лемма доказана.
Пусть  --- насыщенная
--- насыщенная 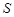 -замкнутая формация,
-замкнутая формация,  --- группа с нормальной силовской
--- группа с нормальной силовской  -подгруппой
-подгруппой  , удовлетворяющая следующим условиям:
, удовлетворяющая следующим условиям:
1) 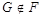 ;
;
2) холлова 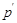 -подгруппа
-подгруппа  -группы
-группы  является максимальной в
является максимальной в  и принадлежит
и принадлежит  ;
;
3) любая собственная подгруппа из 
 -субнормальна в
-субнормальна в  .
.
Тогда  является минимальной не
является минимальной не  -группой.
-группой.
Доказательство. Из условия прямо следует, что  совпадает с
совпадает с  и является минимальной нормальной подгруппой в
и является минимальной нормальной подгруппой в  . Понятно, что каждая
. Понятно, что каждая  -абнормальная максимальная подгруппа из
-абнормальная максимальная подгруппа из  сопряжена с
сопряжена с  и поэтому принадлежит
и поэтому принадлежит  . Пусть
. Пусть  --- произвольная
--- произвольная  -нормальная максимальная подгруппа из
-нормальная максимальная подгруппа из  . Тогда
. Тогда  . Так как
. Так как 
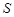 -замкнута, то
-замкнута, то 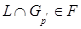 . Подгруппа
. Подгруппа  является собственной в
является собственной в  и по условию
и по условию  -субнормальна в
-субнормальна в  . По теореме,
. По теореме,
 .
.
Итак, каждая максимальная подгруппа из  принадлежит
принадлежит  . Лемма доказана.
. Лемма доказана.
2. Свойства максимальных подгрупп в группах с плотной системой  -субнормальных подгрупп
-субнормальных подгрупп
В данном разделе изучаются свойства максимальных подгрупп конечных групп с плотной системой  -субнормальных подгрупп, где
-субнормальных подгрупп, где  --- произвольная насыщенная
--- произвольная насыщенная 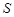 -замкнутая формация.
-замкнутая формация.
Пусть далее  --- некоторое фиксированное упорядочение множества всех простых чисел.
--- некоторое фиксированное упорядочение множества всех простых чисел.
Пусть  --- произвольная насыщенная
--- произвольная насыщенная 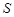 -замкнутая формация,
-замкнутая формация,  ---
--- 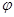 -дисперсивная группа с плотной системой
-дисперсивная группа с плотной системой  -субнормальных подгрупп, не принадлежащая
-субнормальных подгрупп, не принадлежащая  , у которой все
, у которой все  -абнормальные максимальные подгруппы принадлежат
-абнормальные максимальные подгруппы принадлежат  . Тогда справедливо одно из следующих утверждений:
. Тогда справедливо одно из следующих утверждений:
1)  --- максимальная подгруппа в
--- максимальная подгруппа в  ;
;
2)  --- максимальна в
--- максимальна в  -абнормальной максимальной подгруппе из
-абнормальной максимальной подгруппе из  .
.
Доказательство. Пусть  --- группа минимального порядка, для которой лемма не верна. По теореме
--- группа минимального порядка, для которой лемма не верна. По теореме 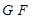 ---
---  -группа. Пусть
-группа. Пусть  ---
---  -абнормальная максимальная подгруппа группы
-абнормальная максимальная подгруппа группы  . Тогда
. Тогда  содержит некоторую
содержит некоторую 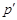 -холлову подгруппу
-холлову подгруппу  . По нашему предположе
. По нашему предположе
|
|
|


