 |
политехнический университет»
|
|
|
|
Кафедра Автоматизации технологических процессов и производств
| Отчет по лабораторной работе № 2 |
| Статистическое оценивание основных характеристик |
| (название лабораторной работы) случайных величин |
| Выполнил | ||
| студент гр. | АТП-12 | |
| Аснина М. Л. | ||
| (подпись) | (Ф.И.О.) | |
| Проверил преподаватель | ||
| Вялых И. А. | ||
| (подпись) | (Ф.И.О.) | |
Пермь 2015
1. Цель работы
Изучить методы статистического оценивания основных характеристик случайных наблюдений.
2. Теоретическая часть
Точечные оценки математического ожидания и дисперсии.
Точечные оценки - это оценки некоторых неизвестных числовых параметров распределения. Они представляют собой числа, полученные путем подстановки выборочных значений 
в формулу для оценивания искомого параметра. Математическое ожидание и дисперсию 
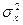оценивают по выборочным среднему 
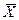и дисперсии 
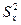, вычисляемым по формулам:
(1)
(2)
Указанные оценки являются состоятельными и несмещенными.
Оценка 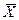является эффективной, a 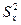стремится к эффективной при 
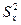. Несмещенность достигается тем, что в знаменателе (2) используется величина, называемая числом степеней свободы выборки 
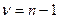, оставшихся после определения 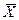, используемого в (2).
Интервальные оценки математического ожидания и дисперсии.
Интервальной оценкой параметра 
называется интервал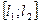 
, границы которого являются функциями выборочных значений и к которому с заданной вероятностью 
принадлежит оцениваемый параметр :
(3)
Интервал 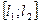называется доверительным, его границы – доверительными пределами, вероятность – доверительной вероятностью, а величина 
- уровнем значимости.
При определении интервальной оценки математического ожидания 
нормальной генеральной совокупности используют t – статистику (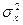 - известна),
|
|
|
(4)
Если дисперсия 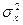неизвестна, то используют ее оценку 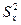и тогда
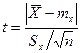(5)
Выборочное распределение t – статистики является t – распределением Стьюдента с числом степеней свободы 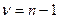. Тогда для случая двусторонней оценки можно записать
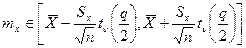(6)
где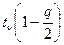 
- табличное значение, найденное по таблице квантилей распределения Стьюдента для уровня значимости 
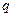и числа степеней свободы .
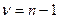Ширина доверительного интервала
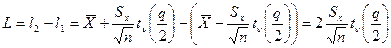(7)
Обычно при определении интервальных оценок используются уровни значимости 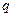= 0,05; 0,1; 0,01 и редко 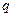= 0,2; 0,001. Например, если доверительный интервал ищется для уровня значимости 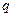= 0,05 
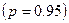, то это значит, что в случае многократно извлечения (наблюдения) выборки объема 
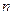ив среднем 100 % построенных но ним интервалов содержат истинное значение .
В некоторых задачах требуется найти одностороннюю оценку , т.е. оценку только сверху или только снизу. При доверительной вероятности односторонние доверительные оценки для математического ожидания будут:
сверху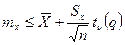 
(8)
снизу 
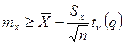(9)
Планирование эксперимента при построении интервальных оценок.
В этом случае планирование эксперимента заключается в определении объема выборки 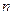, необходимого, при заданной доверительной вероятности, для достижения заданной точности оценивания параметров. Для характеристики точности можно использовать относительную величину
(10)
При оценке доверительного интервала для помимо выражения (6) можно воспользоваться соотношением
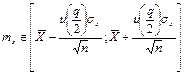(11)
где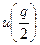 
- аргумент интегральной функции нормированного нормального распределения
(12)
Тогда ширина доверительного интервала
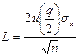(13)
Из формул (10) и (13) получим
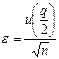(14)
Если задаться предельно допустимой относительной погрешностью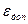 
, то необходимый объем выборки
(15)
3. Практическая часть
3.1 Исходные данные
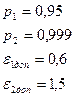
Для доверительной вероятности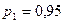 
:
|
|
|
3.2. Расчет необходимого объема выборки для получения оценок математического ожидания 
и среднего квадратичного отклонения 
с заданной точностью.
1) Объем выборки при оценке :
По таблице значений интегральной функции нормированного нормального распределения определим значение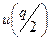 
:
, тогда объем выборки определяется по формуле:
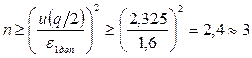
Объем выборки: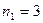 
.
Число степеней свободы: 
2) Объем выборки при оценке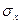 
:
Воспользовавшись соотношением 
, получим:
где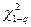 
- квантилии распределения Пирсона.
Следовательно, необходима выборка объема 
3.2 Используя моделирующий алгоритм, снимем две выборки с объемами 
и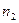 
и для каждой из выборок найдем точечные оценки математического ожидания, дисперсии и СКО.
Значения случайной величины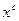 
для выборки с объемами и 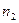получены при помощи программы, написанной в среде MatLab, листинг которой представлен в приложении 1. Значения случайной величины 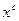приведены в таблицах 1 и 2.
Найдем для 1 выборки (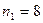
):
Таблица 1 –Значения случайной величины Х для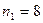
| № | Х |
| 12,9 | |
| 13,9 | |
| 14,2 | |
| 13,6 | |
| 12,6 | |
| 15,9 | |
| 12,5 |
Оценка математического ожидания: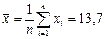 
Оценка дисперсии: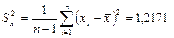 
Оценка среднего квадратичного отклонения: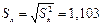 
Найдем для 2 выборки (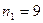
):
Таблица 2 –Значения случайной величины Х для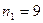
| № | Х |
| 16,4 | |
| 15,2 | |
| 15,9 | |
| 13,7 | |
| 13,5 | |
| 14,3 | |
| 15,1 | |
| 15,9 | |
| 13,9 |
Оценка математического ожидания: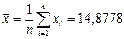 
Оценка дисперсии: 
Оценка среднего квадратичного отклонения: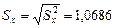 
3.3 Находим интегральную оценку по первой выборке с доверительной вероятностью 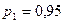и числу степеней свободы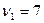 
По таблице квантилей распределения Стьюдента (t - распределение) находим:
Тогда получаем:
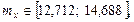
3.4 Находим интегральную оценку 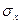по второй выборке с доверительной вероятностью 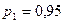и числу степеней свободы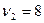 
По таблице квантилей распределения Пирсона находим:
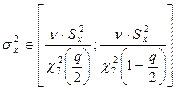
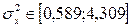
Для доверительной вероятности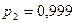 
проведем аналогичные вычисления:
3.5 Необходимый объем выборок
Объем выборки: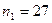 
.
Число степеней свободы: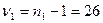 
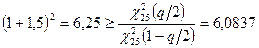
Число степеней свободы: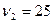 
Объем выборки: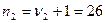 
.
3.6 Точечные оценки математического ожидания, дисперсии и СКО.
Найдем для 1 выборки ():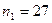
Таблица 3 –Значения случайной величины Х для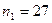
|
|
|
| № | Х |
| 15,1 | |
| 14,3 | |
| 13,7 | |
| 13,7 | |
| 14,3 | |
| 15,5 | |
| 13,8 | |
| 14,2 | |
| 12,7 | |
| 12,7 | |
| 12,3 | |
| 14,2 | |
| 14,1 | |
| 15,6 | |
| 12,3 | |
| 14,5 | |
| 13,4 | |
| 14,3 | |
| 13,9 | |
| 14,4 | |
| 13,7 | |
| 11,8 |
Оценка математического ожидания: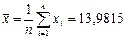 
Оценка дисперсии: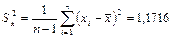 
Оценка среднего квадратичного отклонения: 
Найдем для 2 выборки (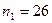 
):
Таблица 4 –Значения случайной величины Х для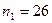
| № | Х |
| 13,2 | |
| 12,4 | |
| 13,9 | |
| 13,3 | |
| 14,5 | |
| 14,2 | |
| 13,7 | |
| 13,1 | |
| 13,6 | |
| 13,9 | |
| 14,2 | |
| 13,6 | |
| 13,8 | |
| 14,7 | |
| 12,4 | |
| 15,1 | |
| 14,4 | |
| 13,2 | |
| 14,7 | |
| 14,8 | |
| 13,3 | |
| 14,8 |
Оценка математического ожидания: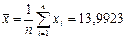 
Оценка дисперсии: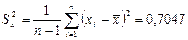 
Оценка среднего квадратичного отклонения: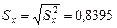 
3.7 Интегральные оценки и 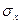с доверительной вероятностью 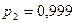и числу степеней свободы 
.
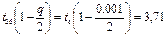
Тогда получаем:
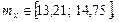
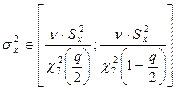
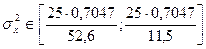
4. Выводы по работе:
В ходе работы созданы выборки случайных величин и получены оценки математического ожидания, дисперсии и среднего квадратичного отклонения, результаты эксперимента обработаны, найдены доверительные интервалы статистических оценок.
Сравнив два эксперимента (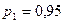 и 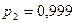), делаем вывод, что при увеличении доверительной вероятности объем выборок увеличивается.
Приложение 1
Листинг программы
clc
clear
X0=14;
n11=8;
n21=9;
n12=27;
n22=26;
X=round((X0+randn(1,1000))*10)/10;%первая выборка для р1
Xv=X(round(rand(1,n11)*1000));
Xsr=mean(Xv);%среднее значение
Sx2=(1/(n11-1))*sum((Xv-Xsr).^2);%дисперсия
Sx=sqrt(Sx2);%среднеквадратичное отклонение
X_2=round((X0+randn(1,1000))*10)/10;%вторая выборка для р1
Xv_2=X(round(rand(1,n21)*1000));
Xsr_2=mean(Xv_2);%среднее значение
Sx2_2=(1/(n21-1))*sum((Xv_2-Xsr_2).^2);%дисперсия
Sx_2=sqrt(Sx2_2);%среднеквадратичное отклонение
X_3=round((X0+randn(1,1000))*10)/10;%первая выборка для р2
Xv_3=X(round(rand(1,n12)*1000));
Xsr_3=mean(Xv_3);%среднее значение
Sx2_3=(1/(n12-1))*sum((Xv_3-Xsr_3).^2);%дисперсия
Sx_3=sqrt(Sx2_3);%среднеквадратичное отклонение
X_4=round((X0+randn(1,1000))*10)/10;%вторая выборка для р2
Xv_4=X(round(rand(1,n22)*1000));
Xsr_4=mean(Xv_4);%среднее значение
Sx2_4=(1/(n22-1))*sum((Xv_4-Xsr_4).^2);%дисперсия
Sx_4=sqrt(Sx2_4);%среднеквадратичное отклонение
|
|
|
|
|
|
