Главная | Обратная связь | Поможем написать вашу работу!

Требования к оформлению контрольной работы

Требования к оформлению контрольной работы

Контрольная работа представлена в 10 вариантах. Номер варианта определяется исходя из списка группы.

Работа выполняется в отдельной тетради, титульный лист который оформлен согласно образцу, приведенному в документе.

При оформлении контрольной работы следует изобразить таблицу (см. Образец) для отметок преподавателя в ходе проверки работы.

Образец

Контрольная работа Вариант …..

№ 1	№ 2	…..	№ 9

При выполнении заданий должны быть учтены следующее указания.

1. Текст каждой задачи необходимо переписать полностью без сокращений или вклеить распечатанный на принтере фрагмент с условием задачи.

2. Составить краткую запись условия (при необходимости),

3. Оформить решение, сопровождая каждый его шаг краткими пояснениями разборчивым почерком (без сокращений слов) и общепринятыми математическими обозначениями.

4. В конце решения записать ответ.

Задачи 1-2 соответствуют тематике лекции 1. В решении необходимо обосновать выбор соответствующей формулы или правила комбинаторики.

Задачи 3-4 соответствуют тематике лекции 2.

Задачи 5-6 на применение теорем сложения и (или) теоремы умножения вероятностей, формулы полной вероятности и (или) теоремы гипотез.

Задача 7 по теме «Дискретные и непрерывные случайные величины»

Задача 8 по теме «Формула Бернулли. Формула Пуассона. Локальная и интегральная теоремы Лапласа»

Задача 9 по теме «Вариационные ряды»

Контрольная работа

Вариант 1

	Сколько различных нечетных пятизначных чисел с неповторяющимися цифрами можно записать, используя цифры 1, 2, 4, 6, 8?
	Из группы в 15 человек выбирают 4-х участников эстафеты 800O400O200O100. Сколькими способами можно расставить спортсменов на этих этапах?
	На отдельных карточках написаны цифры от 1 до 9. Все девять карточек перемешивают, после чего берут четыре из них и раскладывают в ряд друг за другом. Какова вероятность получить при этом четное число?
	Шесть старушек, среди которых, две дружат, вышли во двор поболтать. На скамейке помещаются только четыре из них. Какова вероятность того, что подругам не достанется место на скамейке?
	Четыре орудия стреляют в цель независимо друг от друга. Вероятность попадания в цель каждым из них равна 0, 6. Найти вероятность попадания в цель только двух из орудий.
	Компания по страхованию автомобилей разделяет водителей по классам риска: А, В и С. Предполагается, что из всех водителей, застрахованных в компании, 20% принадлежат к классу А, 40% - к классу В и 40% - к классу С. Вероятность того, что в течение года водитель класса А попадет хотя бы в одну катастрофу, равна 0, 01, для водителя класса В эта вероятность равна 0, 02, а для водителя класса С – 0, 3. Некто страхует свою машину в этой компании и в течение года попадает в катастрофу. Какова вероятность, что он относится к классу В?
	В экзаменационном билете три задачи. Вероятность правильного решения первой задачи 0, 8, второй – 0, 6, третьей – 0, 9. Случайная величина Х – число неправильно решенных задач в билете. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.

	Приведено суммарное число баллов за осенний семестр для каждого студента: 41. 5 42. 3 47. 4 51. 2 52. 3 43. 9 39. 8 36. 2 40. 2 50. 0 49. 1 46. 6 41. 7 57. 5 52. 3 45. 7 32. 4 40. 2 41. 3 43. 5 48. 0 49. 3 57. 4 44. 4 51. 0 49. 8 36. 9 38. 4 44. 4 51. 2 43. 8 50. 6 49. 6 40. 9 50. 8 51. 8 36. 6 39. 2 43. 8 52. 4 39. 6 48. 1 43. 2 50. 8 48. 0 56. 9 50. 6 35. 2 40. 0 32. 1 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении суммарного балла за осенний семестр.

Вариант 2


	Сколько существует вариантов рассаживания вокруг стола 7 гостей на 7 стульях? 3 гостей на 7 стульях?
	Двое друзей, А и В, стоят в очереди из 8 человек. Найдите вероятность того, что: а) А и В стоят рядом; б) между А и В стоят два человека.
	Дано шесть карточек с буквами Н, М, И, Я, Л, О. Найдите вероятность того, что получится слово ЛОМ, если наугад одна за другой выбираются три карточки.
	В сборочный цех завода поступает 40% деталей из первого цеха и 60% -из второго цеха. В первом цехе производится 90% стандартных деталей, а во втором – 95%. Найти вероятность того, что наудачу взятая сборщиком деталь окажется стандартной.

	По одному и тому же маршруту в один и тот же день совершают полет три самолета. Каждый самолет с вероятностью 0, 7 производит посадку по расписанию. Случайная величина Х – число самолетов, отклонившихся от расписания. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.

	Измерена продолжительность работы 50 электрических лампочек, десятков часов: 51 56 69 31 56 49 51 53 74 51 63 48 53 51 64 50 59 84 55 82 55 72 70 54 51 77 98 62 73 55 48 64 52 47 61 70 82 56 54 77 58 52 65 59 68 88 91 79 92 88 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении продолжительности работы электрических лампочек.

Вариант 3

Студенты сдают 5 экзаменов, в том числе 2 экзамена по математике. Сколькими способами можно распределить экзамены так, чтобы экзамены по математике: а) следовали один за другим; б) не следовали один за другим?

В домоуправлении работают 6 человек. Поступило распоряжение о премировании трех сотрудников различными суммами. Сколькими способами это можно сделать?

Натуральные числа от 1 до 20 расставлены случайно. Найдите вероятность того, что числа 5, 6, 7 расположены рядом и притом в порядке возрастания.

Из вазы, где стоят десять красных и четыре розовых тюльпана, выбирают три цветка. Какова вероятность того, что среди выбранных цветов окажутся один красный и два розовых цветка?

Детали поступают в О. Т. К. с двух конвейеров. Производительность второго конвейера вдвое больше первого. В каждой сотне деталей с первого конвейера в среднем две бракованные, а в каждой сотне деталей со второго – 3 бракованных. Найти вероятность того, что взятая наудачу в О. Т. К. деталь бракованная.

Три стрелка сделали по цели по одному выстрелу. Вероятности попадания в цель соответственно равны 0, 5, 0, 6 и 0, 8. Случайная величина Х – число попаданий в цель. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.

4. Измерены излишки общей площади в 40 квартирах, м²:

2. 9	4. 1	4. 1	3. 0	4. 3	4. 2	4. 1	3. 0	4. 1	5. 0
4. 4	5. 9	3. 5	4. 6	3. 4	4. 2	2. 8	3. 4	4. 5	3. 8
4. 7	4. 6	4. 3	4. 1	3. 5	4. 8	3. 6	4. 1	5. 3	3. 6
4. 5	2. 9	5. 0	4. 3	3. 8	3. 5	2. 7	4. 8	4. 1	2. 3

а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор).

б) Изобразить его графически (в виде полигона частостей или гистограммы).

в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности.

г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение.

д) Сделать вывод о среднем значении излишек площади в квартирах.

Вариант 4

	Сколько различных произведений по три различных множителя в каждом можно составить из чисел 2, 3, 5, 7 и 9?
	В почтовом отделении имеются открытки 11 видов. Сколькими способами можно купить 9 открыток?
	Андрей наугад называет натуральное число, не превышающее 200. Ка- кова вероятность того, оно делится на 3, но не делится на 2.
	В ящике 5 синих и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них окажутся 3 белых шара.
	Вероятность попадания в цель из первого орудия равна 0, 9, из второго – 0, 8, из третьего – 0, 7. Найти вероятность того, что при одновременном залпе из трех орудий, будет иметь место: А) только одно поражение цели; Б) хотя бы одно поражение цели.
	За истекший период в торговую фирму поступали телевизоры от трех фирм-поставщиков в следующей пропорции: 2: 5: 3. Каждая фирма дает на свои телевизоры гарантию, идентифицируя их по серийному номеру и дате поставки. Телевизоры первой фирмы требуют ремонта в течение гарантийного срока в 6% случаев, второй и третьей – соответственно в 10% и 4% случаев. Проданный телевизор потребовал гарантийного ремонта, однако потеряны документы, идентифицирующие фирму-поставщика. В какую фирму имеет смысл обратиться в первую очередь?
	В некотором доме 15 семей не имеют автомашины, 20 семей имеют по одной автомашине, одна семья имеет две автомашины. Случайная величина Х – число машин, находящихся в распоряжении одной семьи. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.
	1.
	Измерена продолжительность работы 60 рекламных щитов, десятков часов: 63 48 53 51 64 50 59 84 55 82 55 72 70 54 51 77 98 62 73 55 51 56 69 31 56 49 51 53 74 51 71 66 69 58 60 52 65 87 90 88 48 64 52 47 61 70 82 56 54 77 58 52 65 59 68 88 91 79 92 88 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении продолжительности работы электрических лампочек.

Вариант 5

	Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькими способами он может выбрать приглашенных?
	В расписании уроков на среду для 11 класса должно быть семь уроков: алгебра, геометрия, литература, физика, информатика, история и география. Сколькими способами можно составить расписание на этот день, если уроки алгебры и геометрии должны стоять рядом, а урок истории – последним?
	Из букв слова СОБЫТИЕ, составленного из разрезной азбуки, извлекаются наудачу и складываются друг за другом в порядке их извлечения три карточки. Какова вероятность получить слово БЫТ?
	В лифт шестнадцатиэтажного дома вошли 5 человек. Каждый из них с одинаковой вероятностью выходит на любом этаже, начиная со 2-го. Найдите вероятность того, что все пассажиры выйдут на 6-м этаже.
	Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45 % этих стекол, вторая – 55 %. Первая фабрика выпускает 3 % бракованных стекол, а вторая – 1 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
	Вероятности попадания в мишень для каждого из четырёх стрелков соответственно равны 0, 7; 0, 75; 0, 8; 0, 9. Наугад выбранный стрелок делает один выстрел по мишени. Определить вероятность того, что это был третий стрелок, если цель была поражена.
	Случайная величина Х – суммарное число очков, которые могут выпасть при одном бросании двух игральных костей. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.

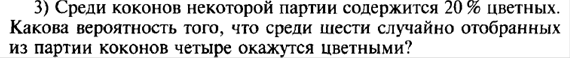
	В результате взвешивания отобранных наудачу 50 клубней картофеля получены следующие результаты (в гр. ): 93 209 135 216 206 80 197 134 145 183 251 84 142 120 177 159 111 185 200 191 96 206 138 213 209 77 200 131 148 180 92 140 126 108 136 86 167 98 172 182 110 128 132 146 150 129 180 165 129 150 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении массы картофельного клубня.

Вариант 6

	Сколькими способами можно составить трехцветный полосатый флаг (три горизонтальных полосы), если имеется материя пяти различных цветов?
	Сколькими способами из группы, в которой учатся 20 студентов, можно выбрать: а) старосту и его заместителя; б) двоих студентов для участия в олимпиаде?
	Владелец сотового телефона забыл 4 цифры кода и набрал их наудачу. Какова вероятность того, что он набрал верный код, если известно, что все эти четыре цифры различны?
	Семеро студентов, среди которых, трое друзей, пошли вместо лекции в кино. Но оказалось, что в кассе осталось только три билета. Какова вероятность, что в кино попадут трое друзей?


	В партии, содержащей 20 деталей, имеются четыре с дефектами. Наудачу взяли для проверки три детали. Случайная величина Х – число дефектных деталей среди отобранных. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.
	В некоторой местности из каждых 100 семей 80 имеют автомобиль. Найти вероятность того, что из 400 семей от 300 до 360 имеют автомобиль.
	В результате измерения длины крыла у 30 воробьев (в см) получены следующие данные: 9, 2 9, 5 8, 1 10, 1 9, 3 9, 7 8, 5 9, 4 10, 3 8, 7 9, 0 9, 8 9, 6 8, 0 8, 2 10, 2 9, 2 8, 9 9, 8 9, 6 7, 9 9, 2 8, 8 10, 6 9, 4 10, 5 9, 1 9, 3 9, 5 10, 4 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении длины крыла у воробьев.

Вариант 7

	Семеро рыбаков отправились на остров на двух лодках. Ночью одна из лодок уплыла. Сколькими способами они могут отправить троих в погоню за уплывшей лодкой?
	В кондитерской имеется 8 видов пирожных. Сколькими способами можно приобрести в ней три разных пирожных?
	Из 60 вопросов экзамена студент подготовил только 50. Какова вероятность того, что из предложенных ему трех вопросов он знает два?
	Восемь друзей распределяют места на скамейке по жребию. Какова вероятность того, что два из них будут сидеть рядом?
	Семь студентов, получив билеты, готовятся к ответу. Знание билетов гарантирует сдачу экзамена с вероятностью 0, 9, а незнание – с вероятностью – 0, 2. Какова вероятность того, что вызванный наудачу студент сдаст экзамен, если Иванов знает 20 билетов из 30, Петров – лишь 15, а остальные студенты знают все билеты?
	Детали поступают в О. Т. К. с двух конвейеров. Производительность второго конвейера втрое больше первого. В каждой сотне деталей с первого конвейера в среднем две бракованные, а в каждой сотне деталей со второго – 3 бракованных. Взятая наудачу в О. Т. К. деталь оказалась бракованная. Найти вероятность того, что она изготовлена на первом конвейере.
	Из ящика с шестью деталями, из которых четыре стандартные, извлекают три детали. Наудачу взяли для проверки три детали. Случайная величина Х – число стандартных деталей среди извлеченных. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.

	Основные фонды 40 предприятий, млрд. руб.: 6. 2 4. 8 3. 6 4. 2 2. 4 4. 9 6. 7 4. 5 2. 7 3. 9 2. 1 3. 5 5. 2 6. 1 3. 3 5. 8 4. 0 7. 3 9. 2 8. 1 2. 8 7. 3 4. 4 6. 6 2. 0 6. 2 7. 0 8. 1 0. 7 6. 8 9. 4 7. 6 6. 3 8. 8 6. 5 1. 4 4. 6 2. 0 7. 2 9. 1 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении основных фондов предприятий.

Вариант 8

	Сколько различных произведений по три различных множителя в каждом можно составить из чисел 2, 3, 5, 7 и 9?
	Сколькими способами можно составить трехцветный (три вертикальные полосы) флаг, если имеется материал красного, желтого, зеленого и черного цветов, причем известно, что одна из полос должна быть зеленой?
	В лотерее разыгрывается 100 билетов. Выигрыши выпали на 20 билетов. Игрок приобрел 5 лотерейных билетов. Найдите вероятность того, что выигрыш выпадет хотя бы на один билет.
	Найдите вероятность того, что дни рождения трех друзей приходятся на разные дни года (не високосного).

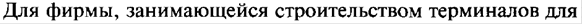
	За истекший период в торговую фирму поступали телевизоры от трех фирм-поставщиков в следующей пропорции: 1: 3: 6. Каждая фирма дает на свои телевизоры гарантию, идентифицируя их по серийному номеру и дате поставки. Телевизоры первой фирмы требуют ремонта в течение гарантийного срока в 15% случаев, второй и третьей – соответственно в 10% и 7% случаев. Проданный телевизор потребовал гарантийного ремонта, однако потеряны документы, идентифицирующие фирму-поставщика. В какую фирму имеет смысл обратиться в первую очередь?
	В экзаменационном билете три задачи. Вероятность правильного решения первой задачи 0, 9, второй – 0, 8, третьей – 0, 7. Случайная величина Х – число правильно решенных задач в билете. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.
	По результатам проверок налоговыми органами установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины 480 предприятий.
	Измерены длины 40 графитовых стержней для карандашей, см: 6. 61 6. 45 6. 54 6. 57 6. 68 6. 58 6. 60 6. 52 6. 56 6. 59 6. 60 6. 54 6. 55 6. 43 6. 47 6. 59 6. 63 6. 56 6. 42 6. 41 6. 56 6. 52 6. 43 6. 40 6. 41 6. 54 6. 47 6. 53 6. 62 6. 46 6. 45 6. 51 6. 46 6. 55 6. 61 6. 68 6. 53 6. 59 6. 51 6. 57 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о средней длине графитовых стержней карандашей.

Вариант 9

	Сколько различных трехзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7 и 9 при условии, что: а) цифры в числе не должны повторяться; б) допускается повторение цифр в числе?
	Каждого из шести студентов можно направить для прохождения практики в одну из трех школ. Сколькими различными способами это можно осуществить?
	В ящике 5 синих и 6 белых шаров. Случайным образом вынимают 4 шара. Найдите вероятность того, что среди них окажутся 3 белых шара.
	Пятнадцать студентов, среди которых, два друга Денис и Стас, пришли на занятия, но в аудитории оказалось только 13 стульев. Какова вероятность того, что Денис и Стас отправятся на поиски стульев?

	В специализированную больницу поступает в среднем 50% больных с заболеванием К, 30% - с заболеванием М, 20% - с заболеванием Р. Вероятность полного излечения болезни К равна 0, 7; болезни М – 0, 8; болезни Р – 0, 9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием М.
	Два стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка равна 0, 6, а для второго – 0, 8. Случайная величина Х – число попаданий в мишень. Найдите: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.
	Для хищника вероятность поимки отдельной жертвы равна 0, 4 при каждом столкновении с жертвой. Каково наивероятнейшее число пойманных жертв в 20 столкновениях?
	Измерена длина тормозного пути (в метрах) 40 автомашин, проходящих технический осмотр: 4. 2 2. 4 4. 9 6. 7 4. 5 2. 7 3. 9 3. 1 5. 8 4. 0 2. 8 7. 3 4. 4 6. 6 2. 0 6. 2 7. 0 8. 1 0. 7 6. 8 9. 4 7. 6 6. 3 8. 8 6. 5 4. 4 4. 6 2. 0 7. 2 9. 1 3. 6 4. 3 4. 9 7. 2 5. 5 4. 1 6. 2 3. 8 6. 1 7. 4 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о средней длине тормозного пути автомашины.

Вариант 10

	Семеро друзей разъехались на новогодние каникулы. Перед Новым годом каждый из них послал всем остальным SMS-сообщения. Сколько всего сообщений было отправлено?
	В ящике 15 деталей, среди которых 6 бракованных. Наудачу выбирается комплект из пяти деталей. Сколько всего комплектов, в каждом из которых две детали бракованные?
	Из колоды в 36 карт вытаскивают четыре карты. Какова вероятность того, что среди них хотя бы одна: а) восьмёрка; б) красной масти?

	Рабочий обслуживает три станка, работающих независимо друг от друга. Вероятность того, что за смену первый станок не потребует внимания рабочего, равна 0, 9, второй – 0, 8, третий – 0, 85. Найти вероятность того, что за смену потребует внимания: А) только один станок; Б) хотя бы один станок.
	На предприятии работают 10 рабочих шестого разряда, 15 рабочих пятого разряда и 5 рабочих четвертого разряда. Вероятность того, что изделие, изготовленное рабочим соответствующего разряда будет одобрено ОТК равна соответственно 0, 95, 0, 9 и 0, 8. Наудачу проверенное изделие оказалось одобрено ОТК. Какова вероятность того, что оно изготовлено рабочим четвертого разряда?
	Два стрелка делают по одному выстрелу в мишень. Вероятность попадания для первого стрелка равна 0, 6, а для второго – 0, 8. Случайная величина Х – число попаданий в мишень. Найти: а) закон распределения этой случайной величины; б) построить многоугольник распределения; в) вычислить математическое ожидание; г) определить дисперсию; д) составить функцию распределения F(x) и построить ее график.
	Фермер отправил на базу 10000 стандартных ящиков с фруктами. Среднее число ящиков, повреждаемых при транспортировке, составляет 0, 02%. Найти вероятность того, что из 10000 ящиков будет повреждено 4.
	В результате взвешивания отобранных наудачу 40 апельсинов получены следующие результаты (в гр. ): 93 209 135 216 206 80 197 134 145 183 251 53 142 120 177 159 111 185 200 191 96 206 138 213 209 170 200 131 148 180 200 180 164 200 192 168 193 128 136 177 а) Составить вариационный ряд (выбрать дискретный или интервальный и обосновать свой выбор). б) Изобразить его графически (в виде полигона частостей или гистограммы). в) Найти и построить выборочные аналоги функции распределения и функции плотности вероятности. г) Найти выборочную среднюю, дисперсию и среднее квадратическое отклонение. д) Сделать вывод о среднем значении массы апельсина.

Воспользуйтесь поиском по сайту: